Question

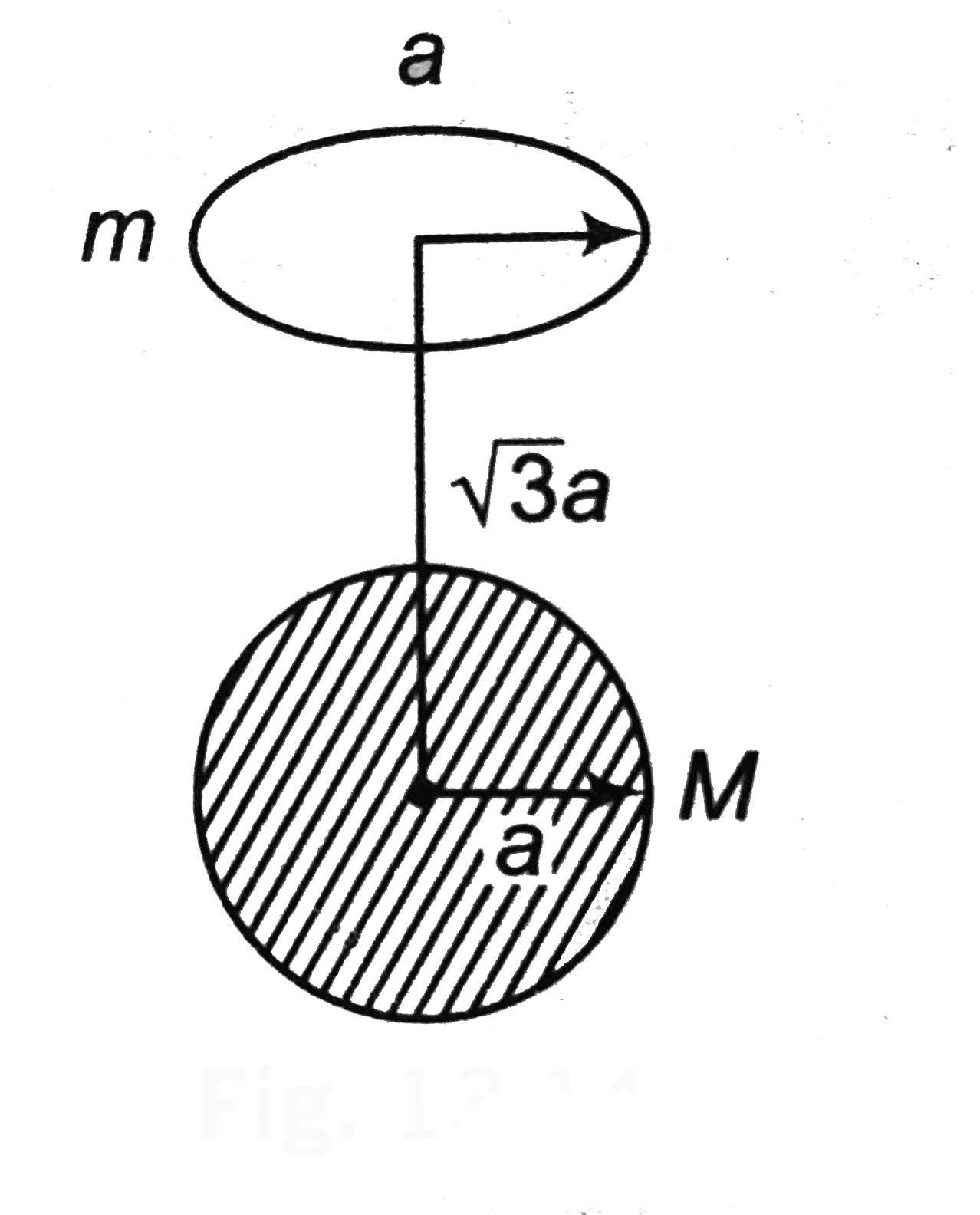
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance $\sqrt{3}$ a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.

Options

A. `(GMm)/(8r^(2))`
B. `(GMm)/(4r^(2))`
C. `sqrt3(GMm)/(8r^(2))`
D. `(GMm)/(8r^(3)sqrt(3))`

Answer

A::B::C

Explanation

To find the gravitational force exerted by a uniform sphere on a uniform ring placed above it, we can follow these steps:

Step 1: Understand the Setup
We have a uniform ring of mass \( m \) and radius \( a \) positioned directly above a uniform sphere of mass \( M \) and radius \( a \). The distance from the center of the sphere to the center of the ring is \( \sqrt{3}a \).

Step 2: Calculate the Gravitational Field due to the Sphere at the Location of the Ring
The gravitational field \( E_g \) due to a spherical mass at a distance \( d \) from its center is given by:
\( E_g = \frac{G M}{d^2} \)
where \( G \) is the gravitational constant, \( M \) is the mass of the sphere, and \( d \) is the distance from the center of the sphere to the point where we are calculating the field.

In this case, the distance \( d \) is \( \sqrt{3}a \):
\( E_g = \frac{G M}{(\sqrt{3}a)^2} = \frac{G M}{3a^2} \)

Step 3: Calculate the Gravitational Force on the Ring
The gravitational force \( F \) exerted by the sphere on the ring can be calculated using the formula:
\( F = m \cdot E_g \)
Substituting the expression for \( E_g \):
\( F = m \cdot \frac{G M}{3a^2} \)

Step 4: Final Expression for the Gravitational Force
Thus, the gravitational force exerted by the sphere on the ring is:
\( F = \frac{G M m}{3a^2} \)

Summary
The gravitational force exerted by the sphere on the ring is given by:
\( F = \frac{G M m}{3a^2} \)