A uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that AC=CD=L3. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
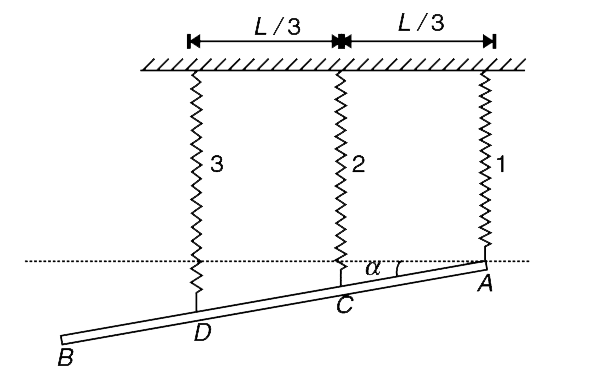
The correct Answer is:T1=Mg12;T2=Mg3;T3=7Mg12
Topper's Solved these Questions
Similar Questions
Let →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View Solution
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .
View SolutionA uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-

View SolutionFind the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x . The mass of the springs is negligible.
View SolutionA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k . The mass of the springs is negligible. The angular frequency of small oscillation is
View SolutionA horizontal metallic rod of mass 'm' and length 'l' is supported by two vertical identical springs of spring constant 'K' each and natural length l_(0). A current 'i is flowing the the rod in the direction shown. If the rod is in equilibrium, then the lengthof each spring in this state is:
View SolutionA horizontal metallic rod of mass m and length l is supported by two vertical identical springs of spring constant k each and natral length i_(0) A current l is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionIn the figure shown a uniform conducing rod of mass m and length l is suspended invertical plane by two conducing springs of spring constant k each. Upper end of springs are connected to each other by a capacitor of capacitance C. A uniform horizontal magnetic field (B0) perpendicular to plane of springs in space initially rod is in equillibrium. If the rod is pulled down and released, it performs SHM. (Assume resistance of springs and rod are negligible)

Find the period of oscillation of rod.
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l//3"and" 2l//3 , and two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure . Find the stretch in each of the spring
View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .
View Solution
