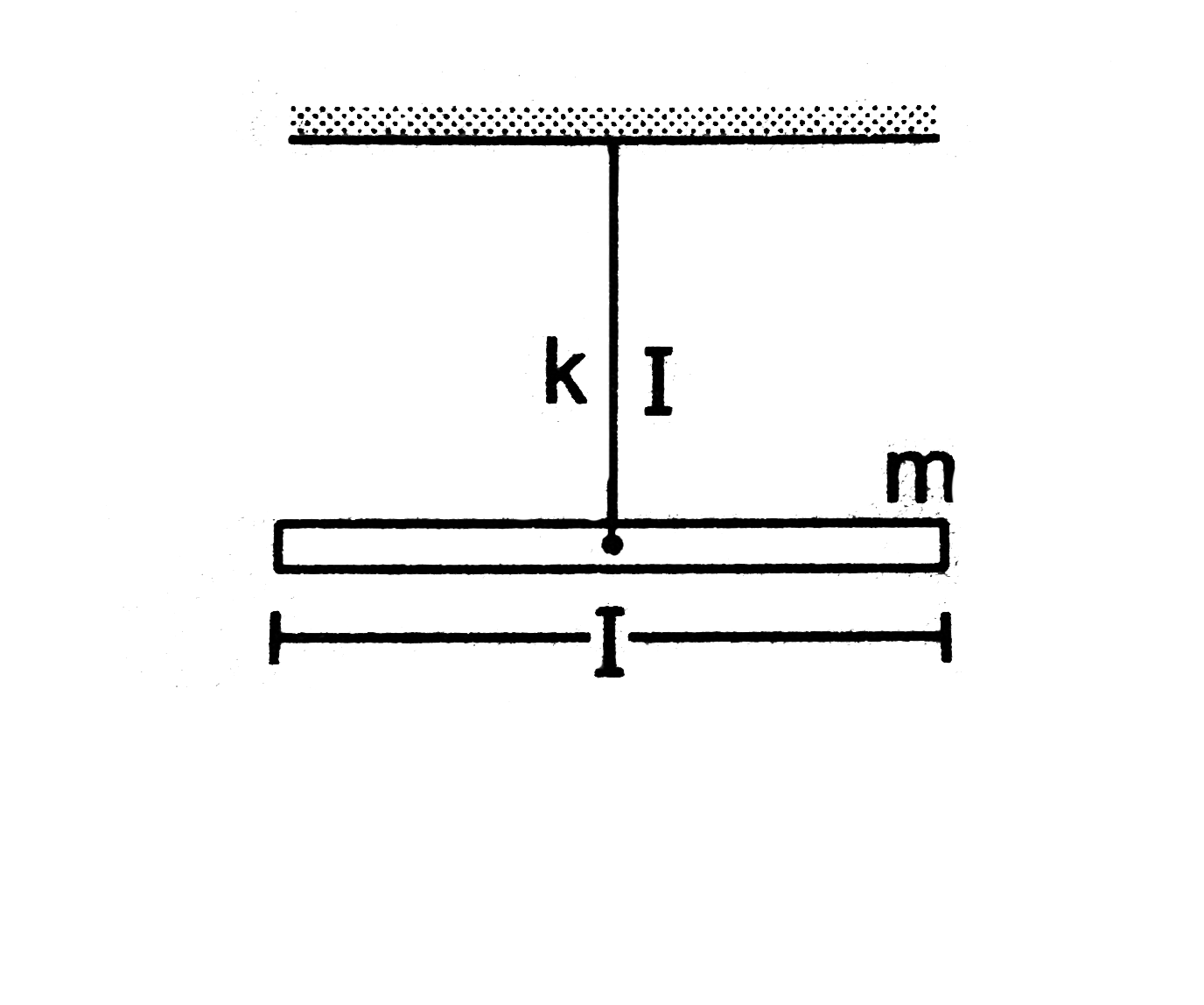
A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time period of the system makes small oscillations in the vertical plane about the suspension point .
 Solution in Tamil
Solution in Tamil
a. The oscillations take place about the horizontal lilne through the point of suspension and perpendicular to the plane of the ure. The moment of inertia of the rod about this line is
ml212+ml2=1312ml2
The time period =2π√Imgl=2π(√13ml212mgl)
=2p(√13l12g)
b. The angular oscillations take place about the suspension wire. The moment of inertia about this line is ml212. The time period is
2π√Ik=2π(√ml212k)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
17 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A person goes to bed at shasrp 10.00 pm every day. Is it an example of periodic motion? If yes, what is the time period? If no why?
View SolutionA student says that he had applied a force F=−k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration.
View SolutionA load of 10 kg is suspended by a metal wire 3 m long and having a cross sectional area 4mm2. Find a. the stress b. the strain and c. the elongation. Young modulus of the metal is2.0×1011Nm−2
View SolutionA uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
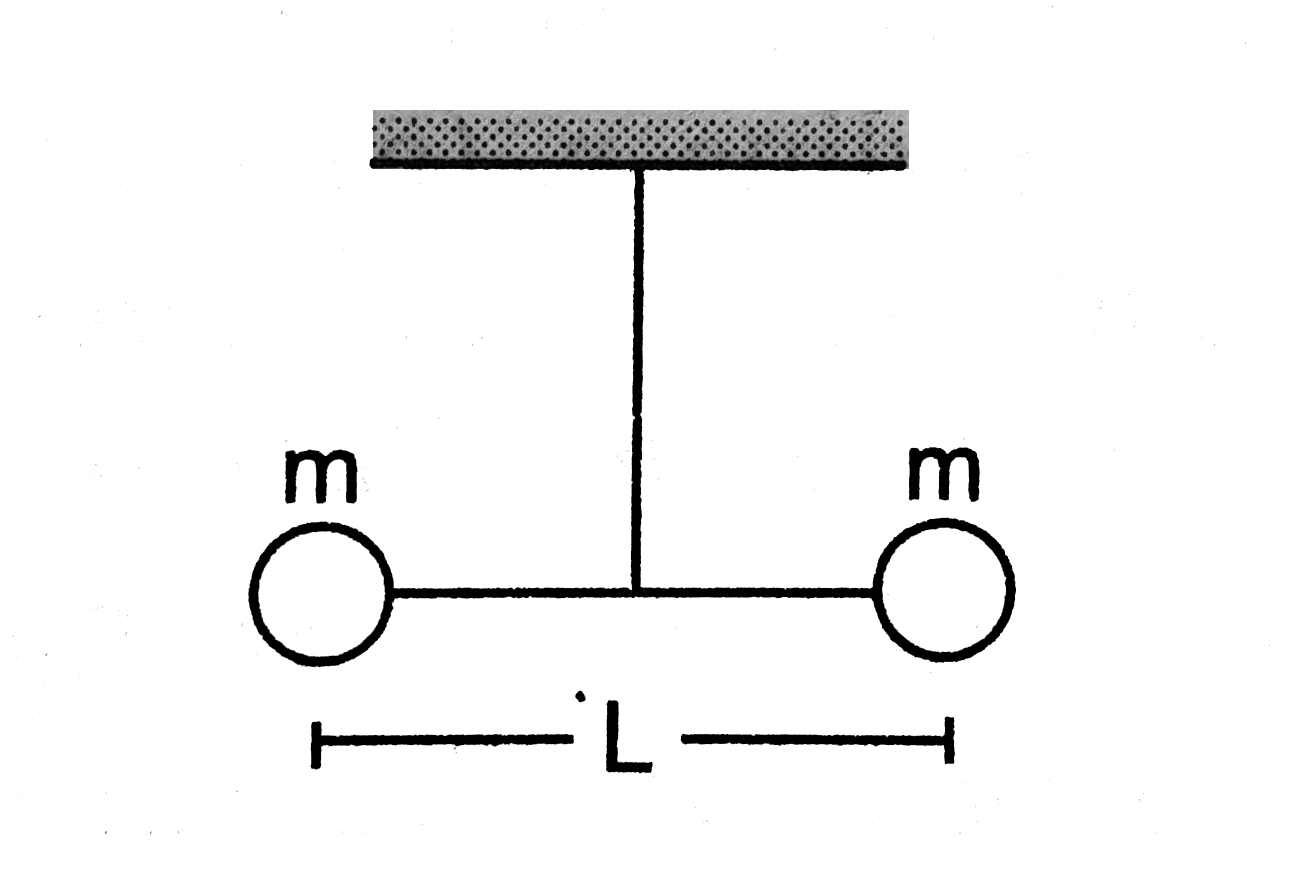
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
View SolutionTwo identacal rods each of length l and mass m weided toeather at right angle and edge suspended from a kinetic sides as shown Angular frequency of small oscillation of the system in its then plane about the total of suspension is
View SolutionA system of two identical rods (L-shaped) of mass m and length l are resting on a peg P as shown in the figure. If the system is displaced in its plane by a small angle theta ,find the period of oscillations:
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

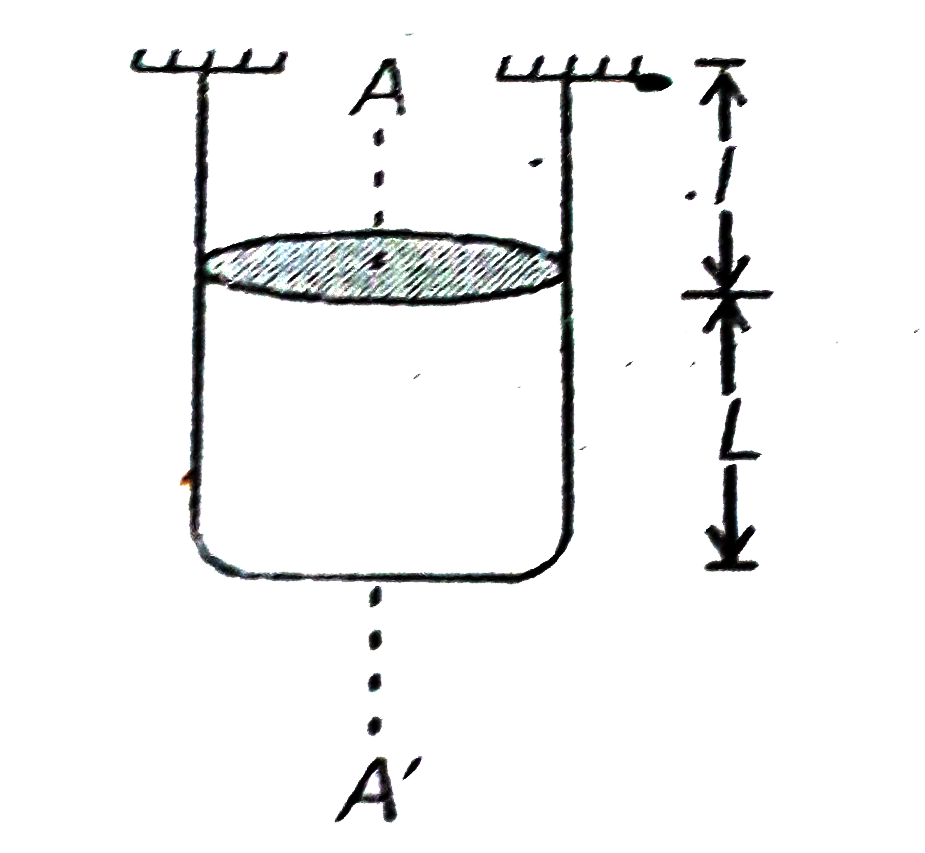
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View Solutionचित्र 22.5 में द्रव्यमान m एवं लम्बाई l वाली एक समरूप छड़ को लम्बाई l वाले पतले तथा नगण्य भार वाले तार द्वारा लटकाया गया है। तार का मरोड़ी नियतांक k है। आवर्तकाल ज्ञात कीजिए यदि (a) छड़ ऊर्ध्वाधर तल में निलंबन-बिंदु के पारित: छोटे दोलन करती है (b) छड़ क्षैतिज तल में अपने केंद्र के पारित: छोटे दोलन करती है।

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
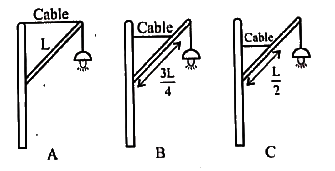
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then

View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'

View Solution
