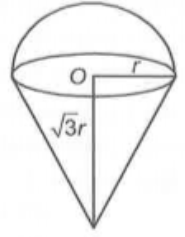
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

1.5R
√3R
3R
2√3R
The correct Answer is:B
yCM=m1y1+m2y2m1+m2
=ρx13πR2h×h4=ρ×23πR3×3R8ρ×13πR2h+ρ×23πR3

⇒h=√3R
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Knowledge Check
A right circular cone whose base radius is 4 is inscribed in a sphere of radius 5. what is the ratio of the volume of the cone to the volume of the sphere?
A0.222:1B0.256:1C0.288:1D0.333:1
Determine the centre of mass of a uniform hemisphere of radius R.
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View SolutionA uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height √3r. If both have same density, then find the position of centre of mass from centre of hemisphere
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

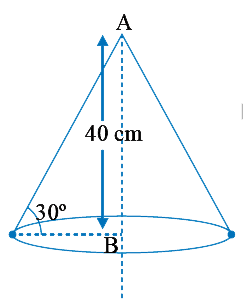
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
View SolutionFind the maximum volume of a cone that can be carved out of a solid hemisphere of radius r.
View Solution
