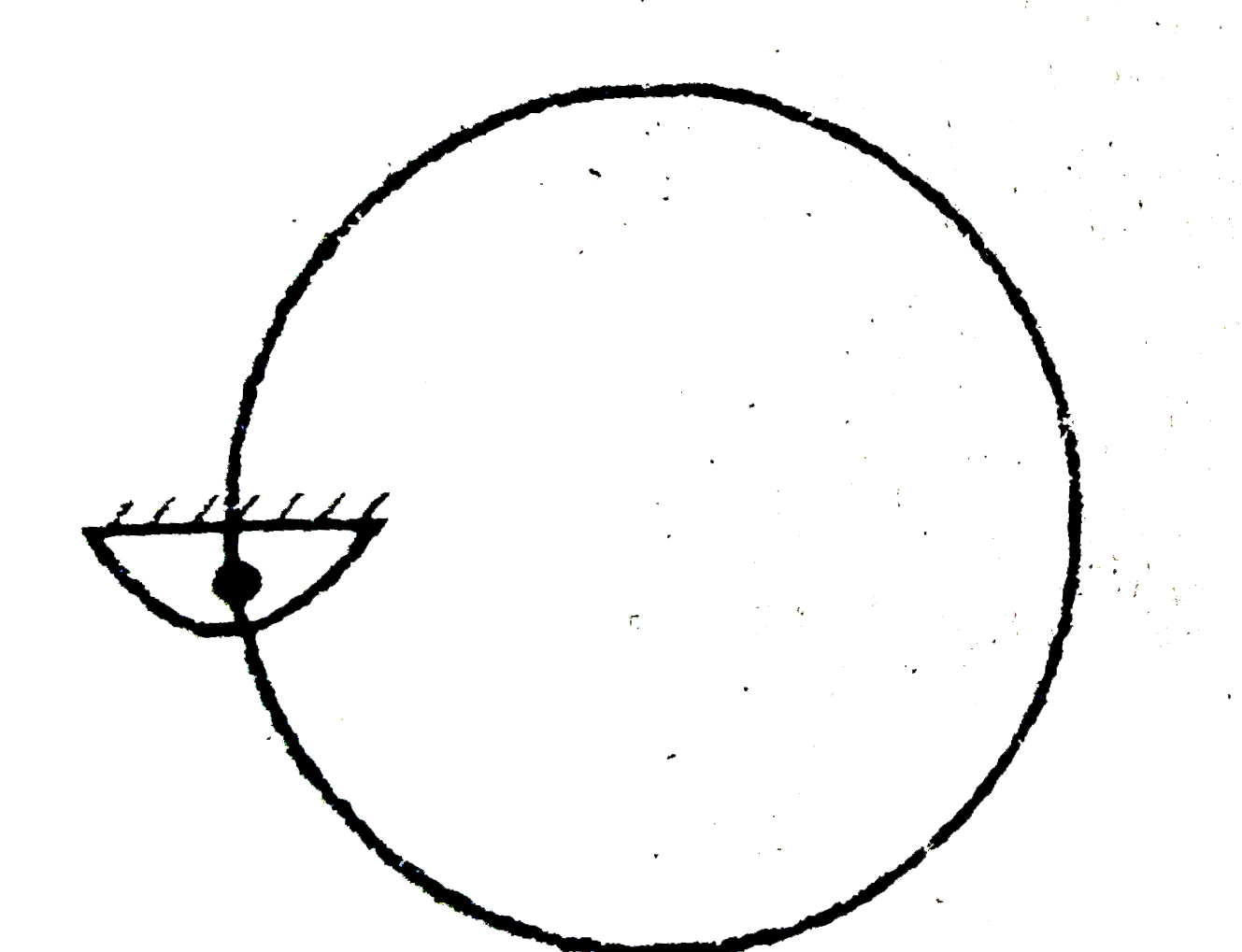
A uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

The correct Answer is:32mg
Applying torque equation about centre of mas
τCM=ICMα………i
⇒NR2=(ICM)α…ii
ICM=mR2+m(R2)2+m(R2)2=32mR2
The CM of system (ring+particle) will be at a distance R/2 from the centre of the ring.
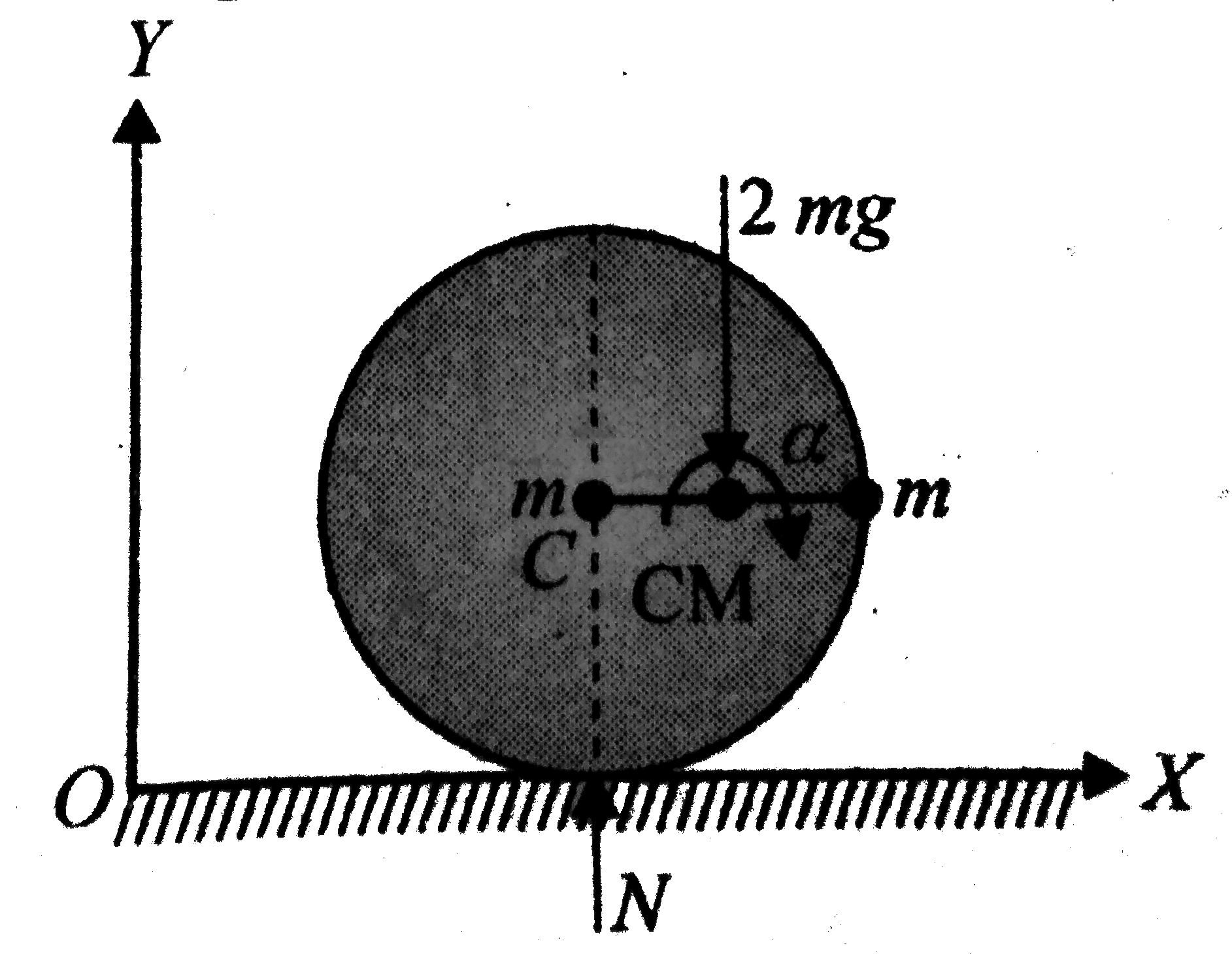
2mg−N=2m(aCM)y .....iii
using constraint acceleration of centre of circle is zero
(ac)y=0
⇒R2α=(aCM_(y)).......iv
Form ii, iii and iv we get
N=32mg
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
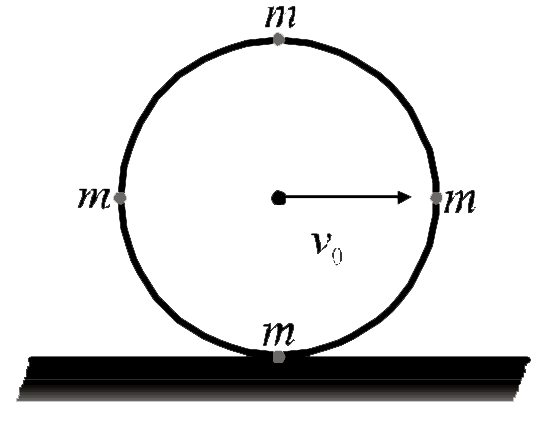
A ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
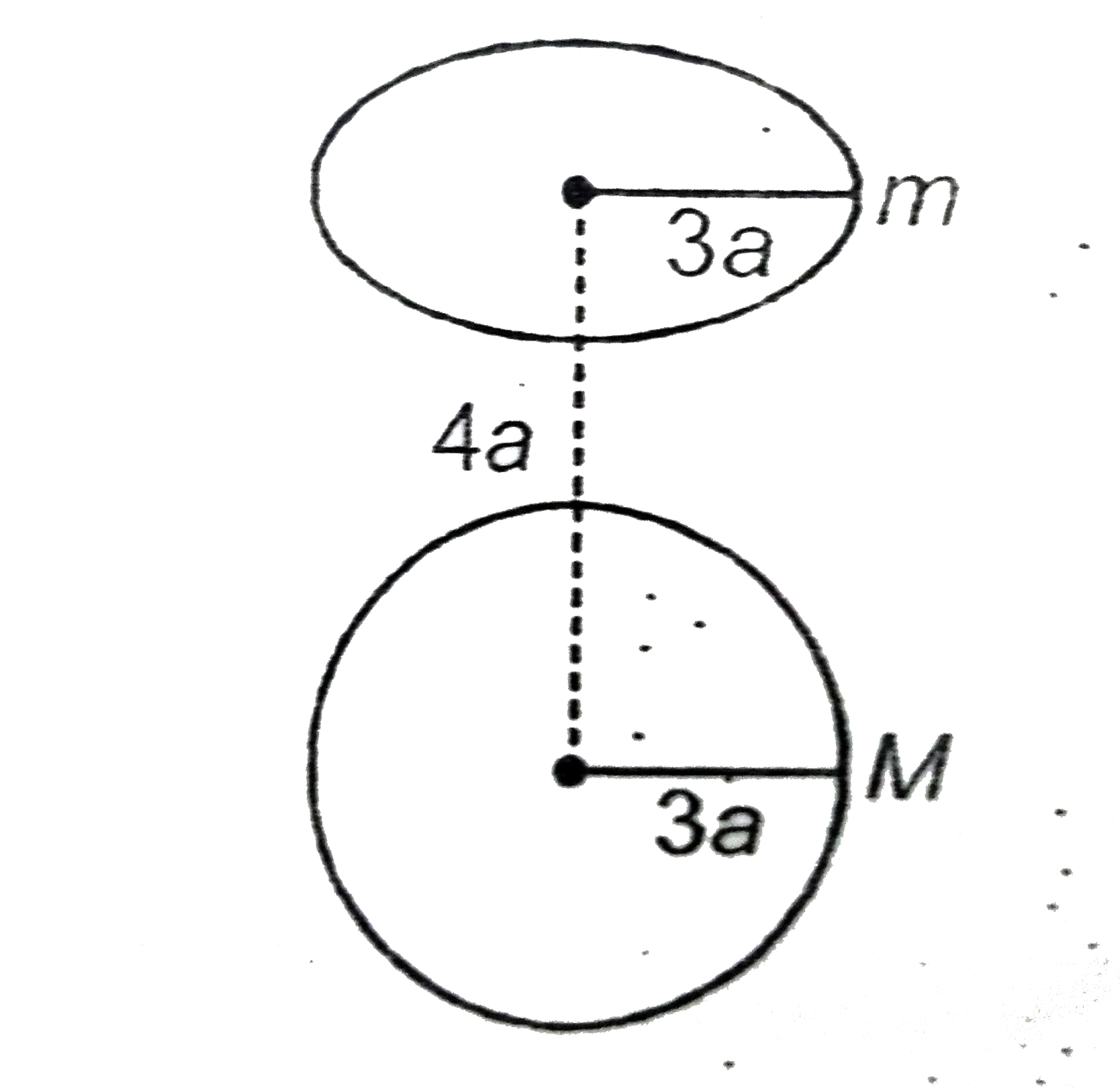
View Solution
Knowledge Check
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
Athe particle will execute S.H.M inside the shellBthe particle will oscillate inside the shell, but the oscillations are not simple harmonicCthe particle will not oscillate, but the speed the particle will go on increasingDnone ot theseA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
A√GMaB√GM2a(mM)C√GM2a(Mm)D√GMa(MM+m)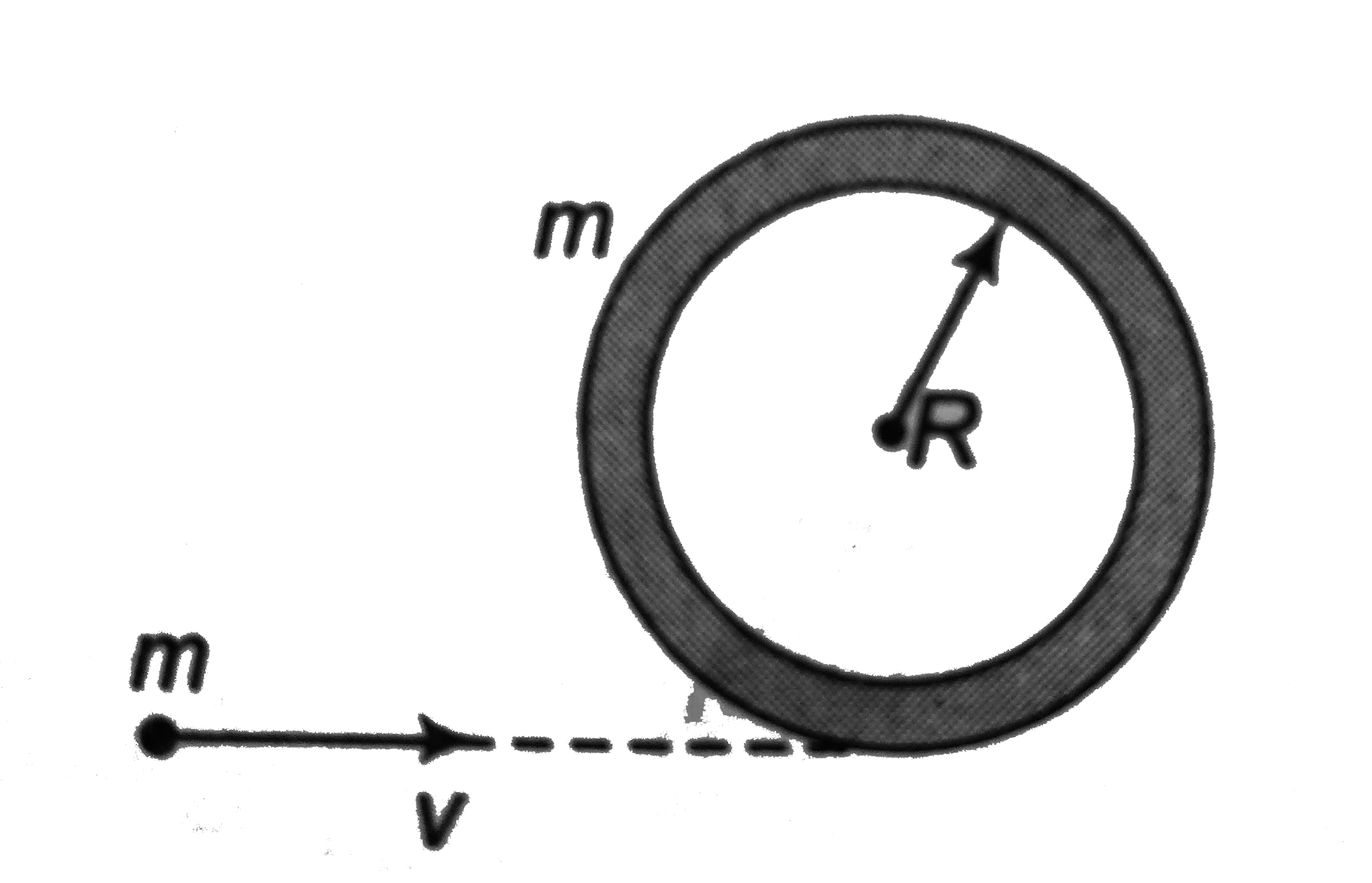
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring isAv2RBv3RC2v3RD3v4R
A ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .
.
View SolutionA ring of mass 0.8 kg and radius 1m is hinged at a point on its periphery such that the hinge is at the same horizontal level as its centre. The ring in vertical plane and released. Find the force exerted (in N) by the hinge on the ring just after the release.
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View Solution
