A uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
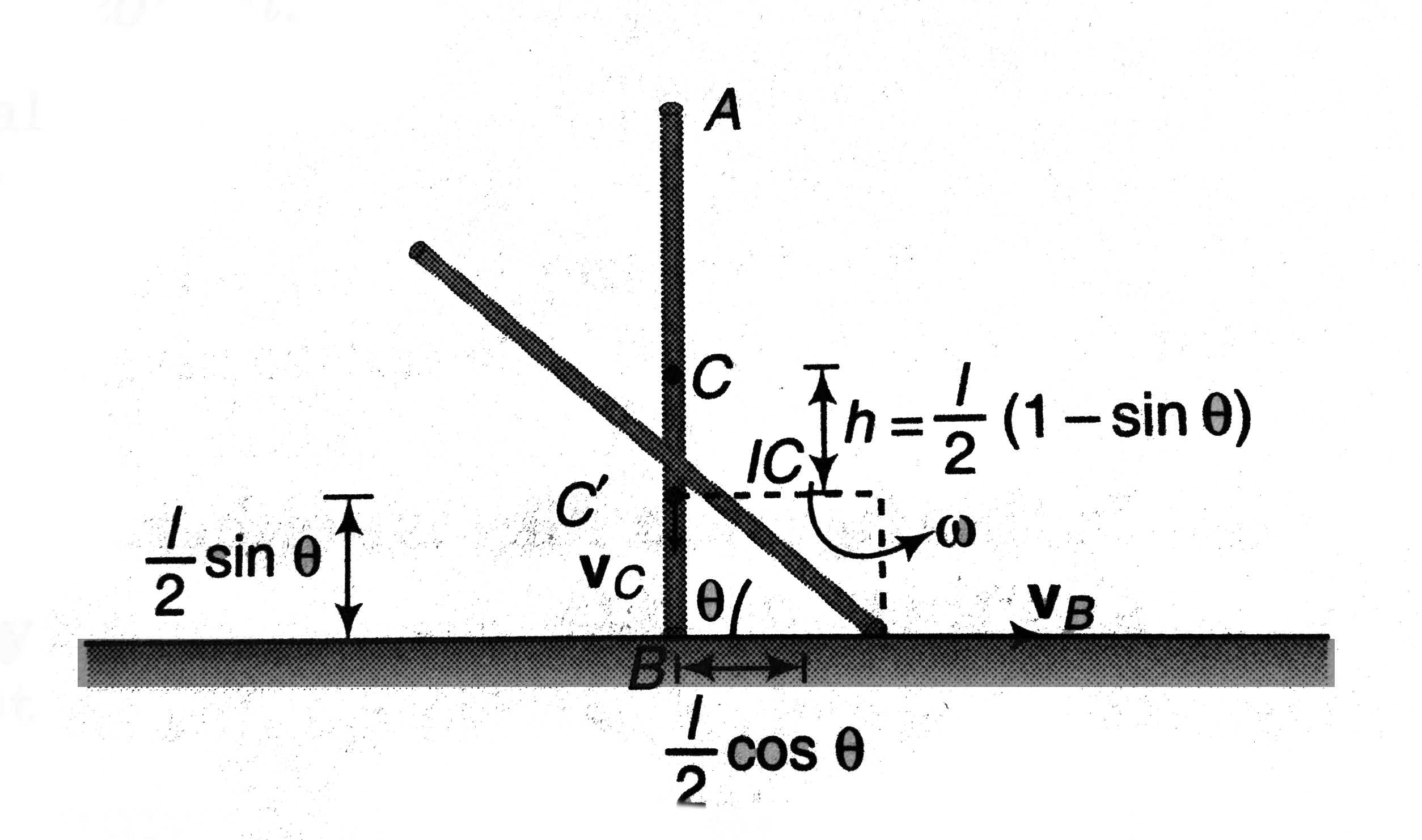
As The floor is smooth mechanical energy of the rod will remain conserved. Further no horizontal force acts on the rod, hence the centre of mass moves vertically downwards in a straight line. Thus velocities of COM and the lower end B are in the directions shown in figure. The location of IC at this instant can be found by drawing perpendiculars to VC and VB at respective points. Now the rod may be assumed to be in pure rotational motion about be assumed to be in pure rotational motion about IAOR passing through IC with angular speed ω.
Applying conservation of mechanical energy. Decrease in gravitational potential energy of the rod = increase in rotational kinetic energy about IC
∴mgh=12IICω2
or mg(l)2(1−sinθ)=12(ml212+ml24cos2θ)ω2
Solving this equation we get
ω=√12g(1−sinθ)l(1+3cos2θ)
Now. |VC|=(l2cosθ)ω
=√3gl(1−sinθ)cos2θ(1+3cos2θ)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass M and length L is standing vertically along the y-axis on a smooth horizontal surface as shown. A small disturbance causes the lower end to slip on the smooth horizontal surface and rod starts falling. The path followed by centre of mass of the rod during the fall is

View SolutionA uniform thin rod of mass m and length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbane at t = 0 causes the lower end t slip on the smooth surface along the positive x-axis, and the rod starts falling.
(i) What is the path followed by the centr of mass of the rod during its fall?
(ii) Find the equaiton to the trajectory of a point on the rod shape of the path of this point?
View Solution
Knowledge Check
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpmlA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
AmglBmgl/2Cmgl4D2mglA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 A2πmlPBπml3PCπml12PD2πml3P
A2πmlPBπml3PCπml12PD2πml3P
A uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

The point about which rod rotates just after impulse being applied is located at
View Solution
