(a) Using Gauss law, derive expression for electric field due to a spherical shell a uniform charge distribution $σ$ and radius R at a point lying at a distance r from the centre of shell, such that
(i) $O < r < R, and$
(ii) $r > R$ .
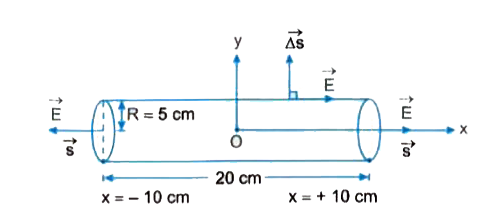
(b) An electric field is uniform and acts along +x direction in the region of positive x. It is also uniofrm with the same magnitude but acts in -x direction in the region of negative x. The value of the fleld is E= 200 N/C for $x > 0 and E = - 200 N / C for x < 0$ . A right circular cylinder of length 20 cm and radius 5 cm has its centre at the origin and its axis along the x-axis so that one flat face is at x =+ 10 cm and the other is at x=-10 cm.
Find :
(i) The net outward flux through the cylinder.
(ii) The net change present inside the cylinder.

Text Solution

Verified by Experts

(a) (i) Consider a hollow charged conducting sphere of radius R and having charge Q. To find electric field at a point P inside the shell, consider a sphere through point P and having centre O, i.e, r= OP $(where O < r < R)$ as the Gaussian surface.
The electric flux through the Gaussian surface $ϕ_{E} = \oint \to E . ˆ n d s = E 4 π r^{2} ... . (i)$
According to Gauss theorem, total electric flux should be
$ϕ_{E} = \frac{1}{ε_{0}} (charged enclosed) = 0$
Thus, $ϕ_{E} = E .4 π r^{2} = 0$
[Since the Gaussian surface is not enclosing any charge) Thus, $ϕ_{E} = E .4 π r^{2} = 0$
$\Rightarrow E = 0$

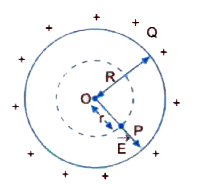
(ii) To find electric field intensity at a point Poutside the shell situated at a distance $r (r > R)$ from the centre of shell, consider a sphere of radius r as the Gaussian surface. All points on this surface are equivalent relative to given charged shell and, thus, electric field E at all points of Gaussian surface has same magnitude E and $\to E$ and i are parallel to each other.
Total electric flux over the Gaussian surface
$ϕ_{E} = \oint \to E . ˆ n d x = E .4 π r^{2} ... ... (i)$

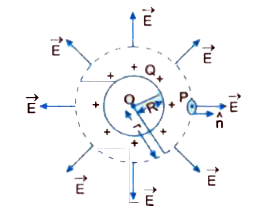
According to Gauss.s theorem, $ϕ_{E} = \frac{1}{\in_{0}} (charged enclosed) = \frac{Q}{\in_{0}}$ ........(ii)
Comparing (i) and (ii), we get
$E .4 π r^{2} = \frac{Q}{\in_{0}} or E = \frac{Q}{4 π \in_{0} r^{2}}$
If surface charge density of shell be $σ then Q = 4 π R^{2}, σ$ and therefore
$E = \frac{4 π R^{2} σ}{4 π \in_{0} r^{2}} = \frac{σ R^{2}}{\in r^{2}}$
(b) The situation is shown in the given figure. Here,
$E = 200 N C^{- 1}$ length of cylinder l=20cm, 0.2m, radius of cylinder R=5cm, =0.05m
(i) As shown in figure the net outward electric flux is along x-axis and hasa value
$ϕ_{E} = 2 E △ s$
$= 2 E π R^{2}$
$= 2 \times 200 \times 3.14 \times {(0.05)}^{2}$
$= 3.14 N m^{2} C^{- 1}$
(ii) As per Gauss law, net charge present inside the cylinder
$q = \in_{0} \times ϕ_{E} = (8.854 \times 10^{- 12}) \times 3.14 = 2.78 \times 10^{- 11} C$

Updated on:21/07/2023

Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A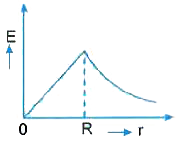
B
C
D