A vertical U-tube has a liquid up to a height h. If the tube is slowly rotated to an angular speed ω=√gh find the (i) heights of the liquid column, ii pressures at the points 1,2 and 3 in the limbs in steady state.

The correct Answer is:ρgh4
dpdx=ρ(ω2x)⇒dp=ρω2xdx
integrating both sides, we get

∫p3p1dp=ρω2∫2h−hxdx
p3−p1=ρω2[x22]=ρω22[4h2−h2]
ρ(h3−h1)=3ρω2h22=3ρ2h2(gh)
h3=h1=3h2..........i
But h3+h1=2h.........ii
After solving h3=7h4 and h1=h4
p3=p0+rog(7h4) and p1=p0+ρg(h4)
and p3−p2=ρω22[x2]20=ρω22(rh)2
p3−p2=ρ2(gh).4h2=2ρgh
p0+ρg(7h4)−p2=2ρgh⇒p2=p0−ρgh4
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
A vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
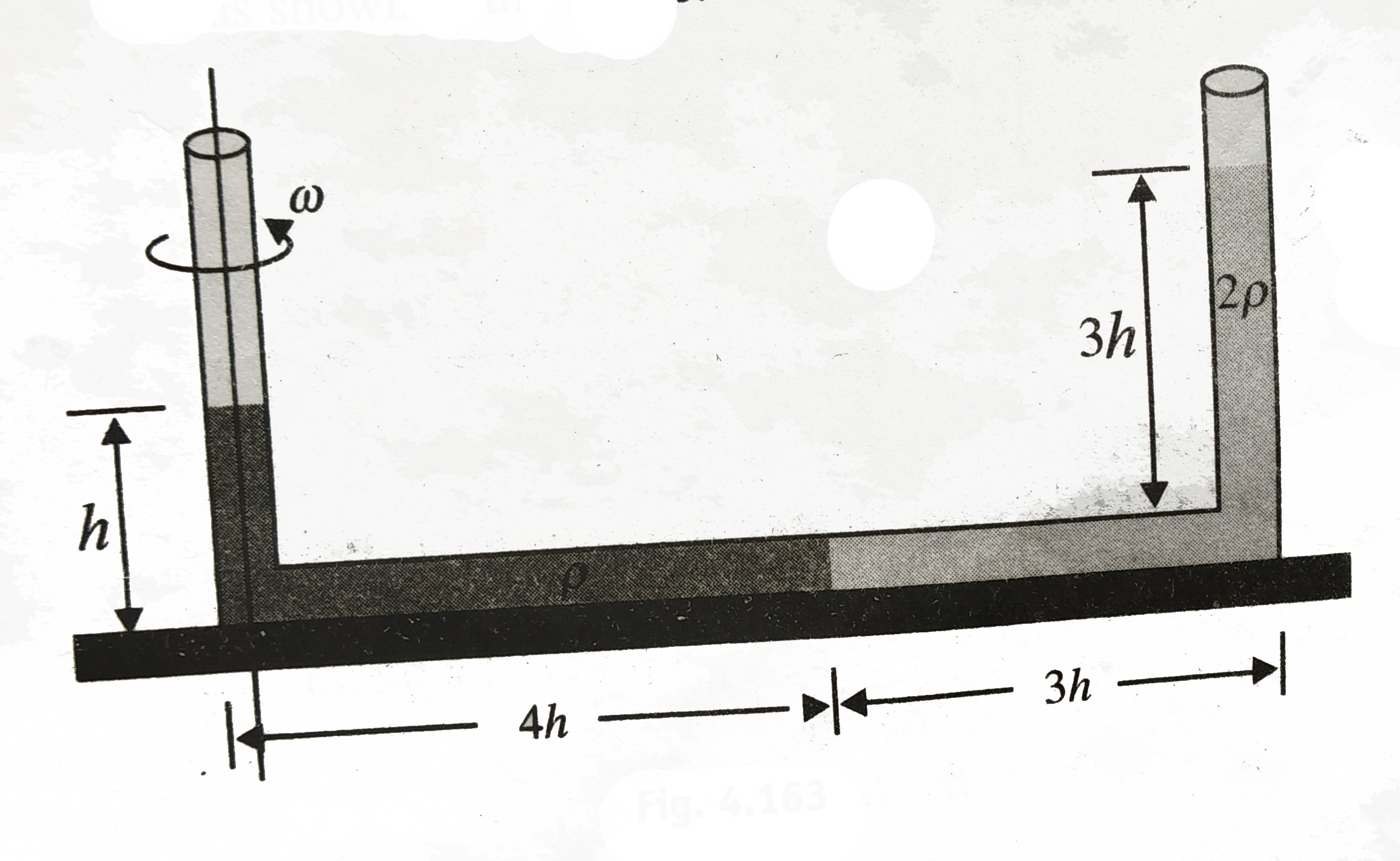 View Solution
View Solution
A liquid of density ρ is rotated by an angular speed ω as shown in figure,Using the concept of pressure equation, find a relation between h1,h2,x1 and x2.View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
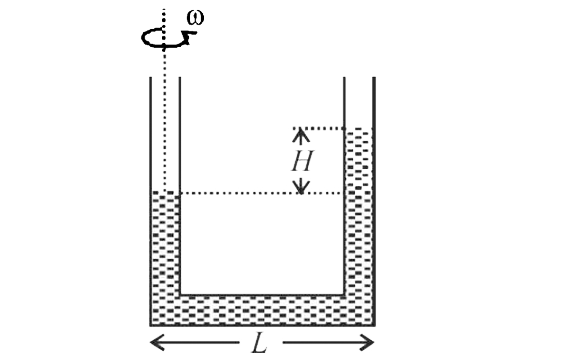 View Solution
View SolutionA vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
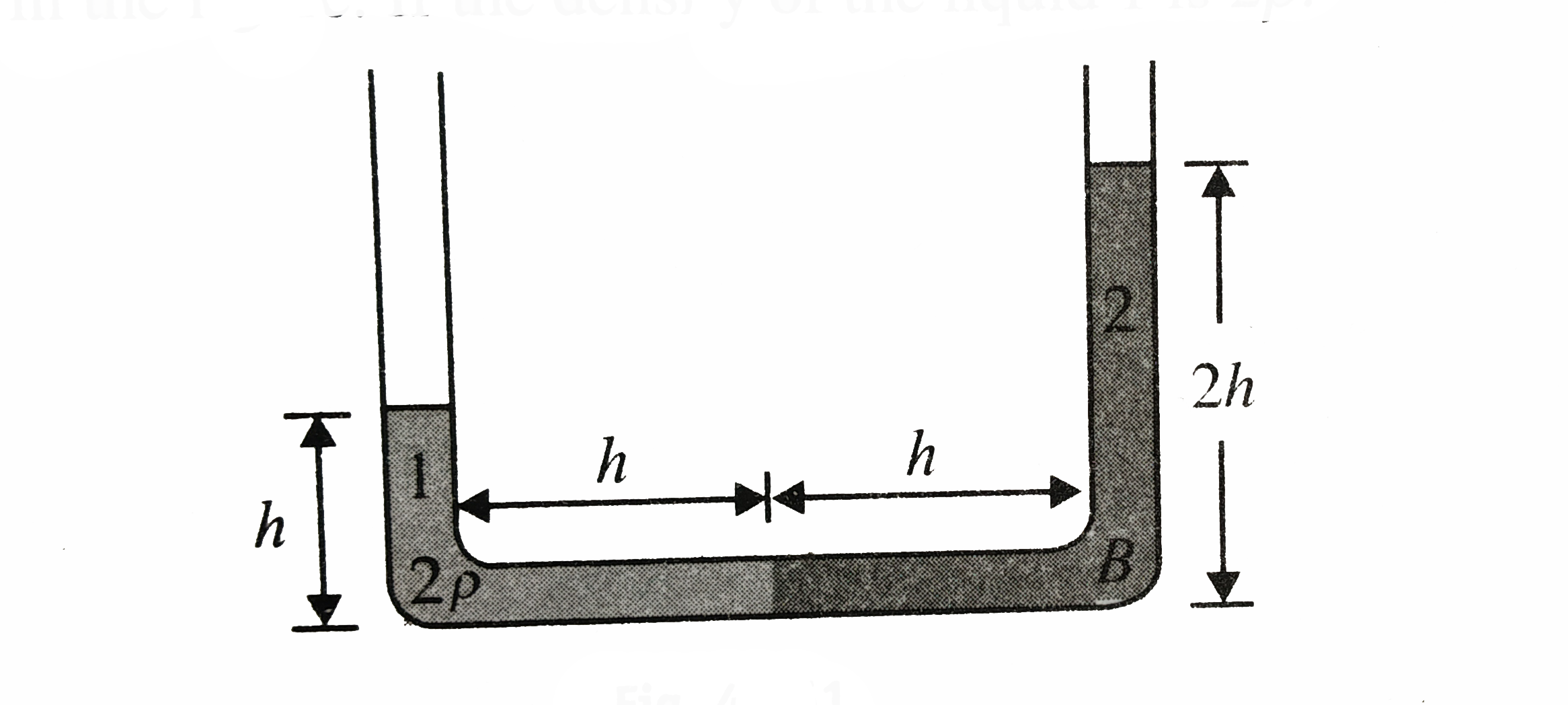
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.View SolutionA U-tube contains a liquid to a height of 9.8 cm in one of the limbs. The tube is vertical. If the liquid on one side is depressed a little and released its motion in the tube is simple harmonic motion. Find its period.
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View SolutionA container (see figure) contains a liquid upto a height h. The density of the liquid is The gauge pressure at point P is ρghx. Find the value of x
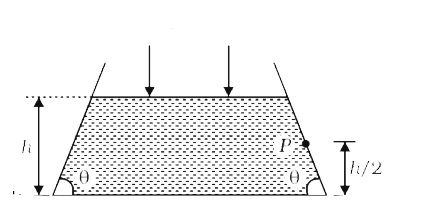 View Solution
View SolutionAn air column closed in a tube sealed at one end by a Hg column having height h. When the tube is placed with open end down, the height of the air column Iis l1. If the tube is turned so that its open end is at the top, the height of the air column is l2. What is the atmospheric pressure (P0).
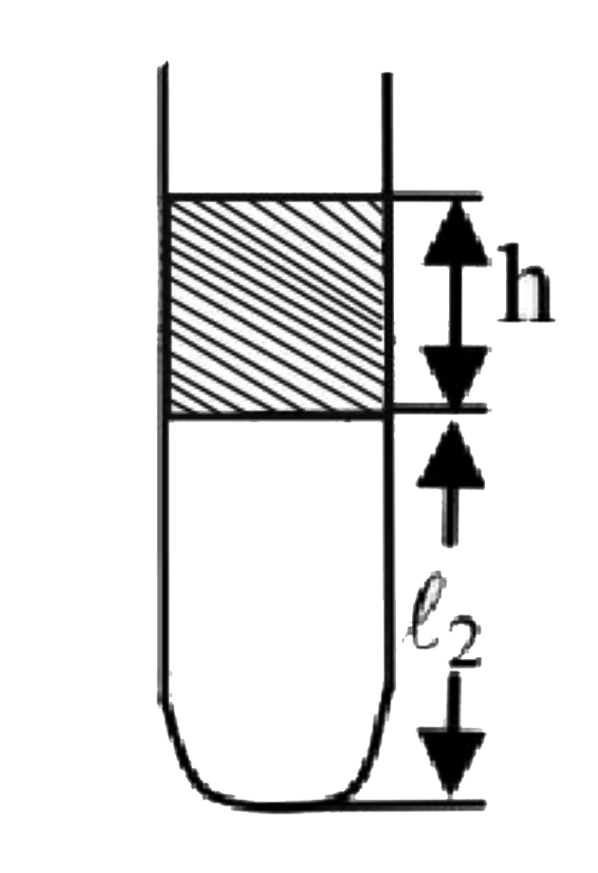 View Solution
View SolutionA cylinder of radius R and height H is foam unknown height h. When is rotated at an unknown constant angular velocity ω, the base of the cylinder gets exposed when the liquid just starts spilling out, as shown in Fig.
a. Find the height h of the liquid.
b. Find the angular speed w of the cylinder.
 View Solution
View SolutionLength of a horizontal arm of ends of both the vertical arms pressure P0=105N/m2. A liquid of density ρ=103kg/m3 is poured in the tube such that liquid just fills the horizontal part of the tube as a shown in Fig. Now one end of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm with angular speed ω0=√40/3rad/sec. If length of each vertical arm is a=1m and in the sealed end liquid rises to a height y=1/2m, find pressure in the sealed tube during rotation. (in ×105N/m2)
 View Solution
View Solution

