A very long wire carrying a current is bent at right angles. Find the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the Point of bending at a distance from it.
The correct Answer is:B
To solve the problem of finding the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the point of bending at a distance l=35cm from it, we can follow these steps:
Step 1: Understand the Configuration
We have a long straight wire that is bent at right angles. The magnetic field due to a straight wire carrying current can be calculated using the Biot-Savart law or Ampere's law. The point of interest is located at a distance l from the bending point of the wire.
Step 2: Magnetic Field due to a Straight Wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Step 3: Calculate the Magnetic Field from Each Segment
Since the wire is bent at right angles, we can treat the two segments of the wire separately.
1. For the first segment (straight wire):
- The distance from the point of bending to the point of interest is l=35cm=0.35m.
- The magnetic field due to this segment at the point is:
B1=μ0I2πl=(4π×10−7)×5.02π×0.35
Simplifying this gives:
B1=(4×10−7)×5.02×0.35=20×10−70.7=20×10−77≈2.857×10−7T
2. For the second segment (perpendicular wire):
- The magnetic field due to the second segment at the point of interest is zero because the distance is effectively zero (the point lies on the perpendicular bisector of the segment).
Step 4: Combine the Magnetic Fields
Since the magnetic field from the second segment is zero, the total magnetic induction at the point is simply the magnetic field from the first segment:
Btotal=B1+B2=B1+0=B1≈2.857×10−7T
Final Answer
The magnetic induction at the point is approximately:
B≈2.857×10−7T
We have a long straight wire that is bent at right angles. The magnetic field due to a straight wire carrying current can be calculated using the Biot-Savart law or Ampere's law. The point of interest is located at a distance l from the bending point of the wire.
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space, approximately 4π×10−7T m/A.
Since the wire is bent at right angles, we can treat the two segments of the wire separately.
- The distance from the point of bending to the point of interest is l=35cm=0.35m.
- The magnetic field due to this segment at the point is:
B1=μ0I2πl=(4π×10−7)×5.02π×0.35
Simplifying this gives:
B1=(4×10−7)×5.02×0.35=20×10−70.7=20×10−77≈2.857×10−7T
- The magnetic field due to the second segment at the point of interest is zero because the distance is effectively zero (the point lies on the perpendicular bisector of the segment).
Since the magnetic field from the second segment is zero, the total magnetic induction at the point is simply the magnetic field from the first segment:
Btotal=B1+B2=B1+0=B1≈2.857×10−7T
The magnetic induction at the point is approximately:
B≈2.857×10−7T
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A long wire carrying a current i=2A is bent at right angles . The magnetic field lying on a perpendicular normal to the plane of the wire draw through the point of bending at distance 1 m form it is ………….Tesla.
View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
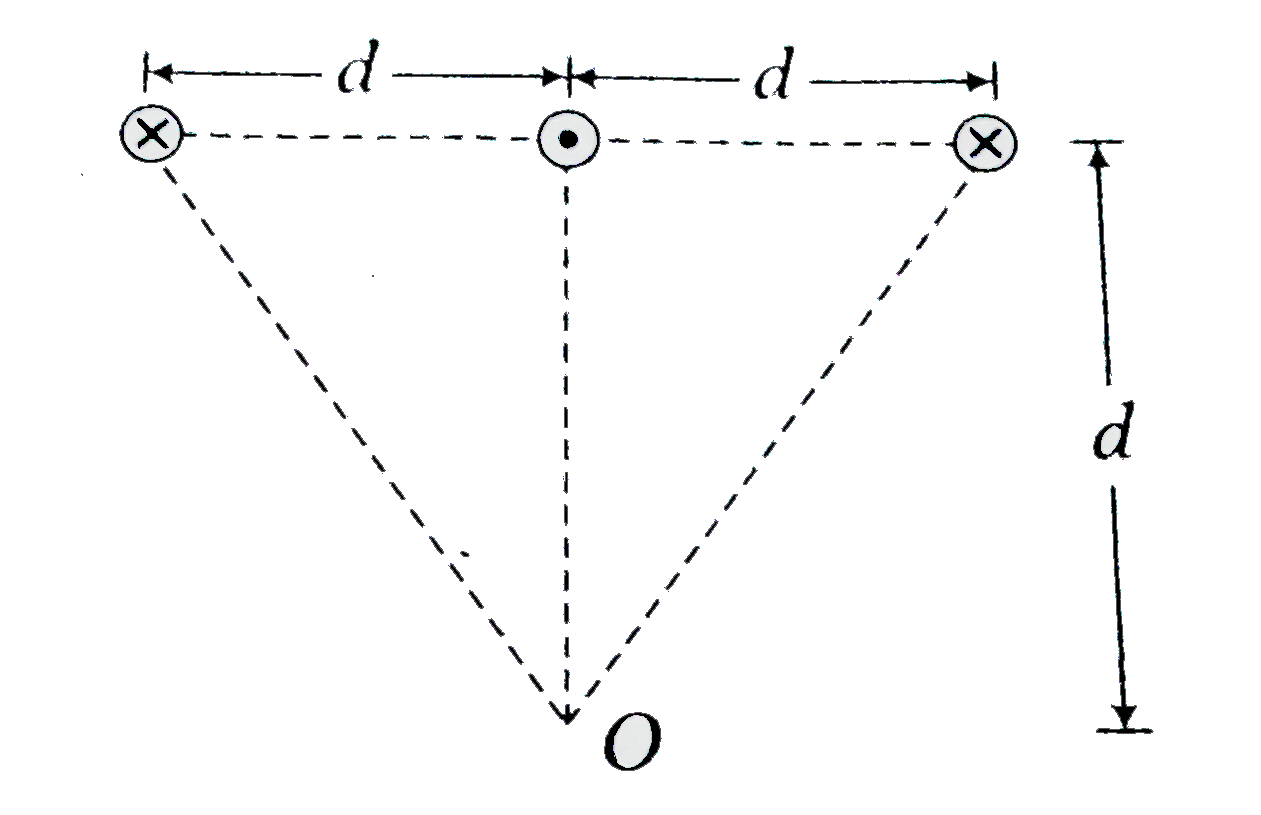 View Solution
View SolutionA long wire carrying a current i is bent to form a plane angle alpha.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is
 View Solution
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
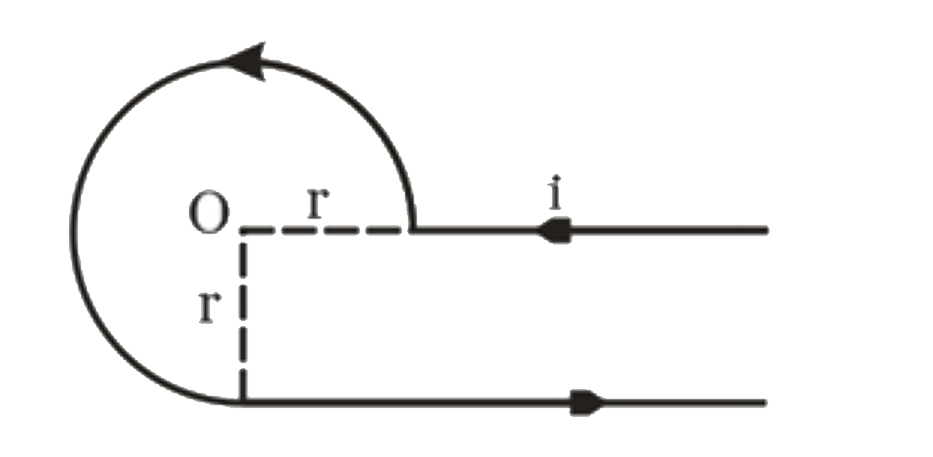 View Solution
View SolutionThe magnetic induction at the point O, if the wire carries a current I, is
 View Solution
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA long cylindrical wire carrying current of 10A has radius of 5mm find its its magnetic field induction at a point 2mm from the centre of the wire
View SolutionA conducting wire carries 5A current. Its lenghts 6cm. Then the magnitic field intensity at a distance of 4cm from the wire on the perpendicular bisector of the wire is
_2019_CBT8_E01_002_Q01.png) View Solution
View Solution

