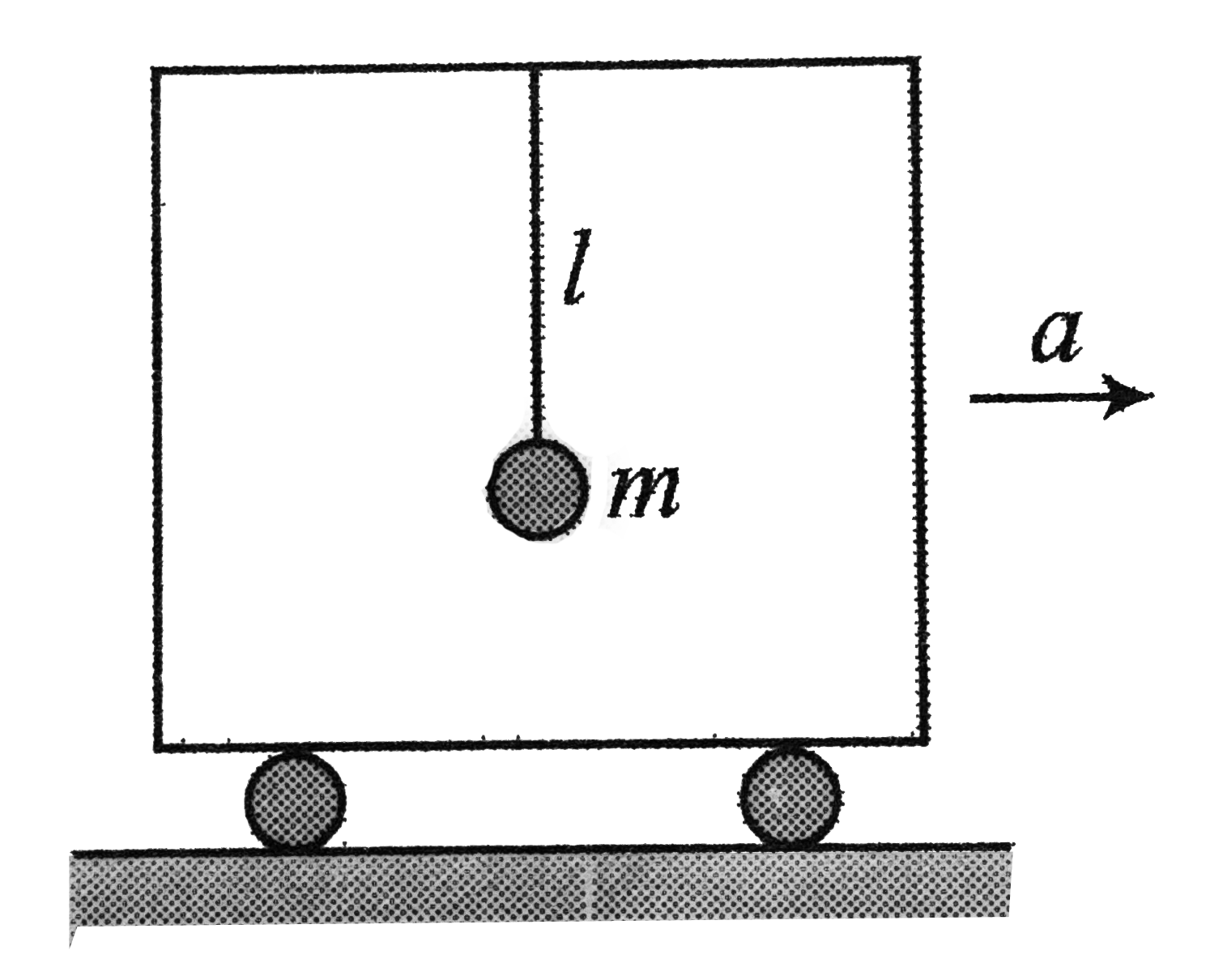
A wagon of mass can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
The correct Answer is:A, B
To solve the problem, we will use the principles of conservation of momentum and the work-energy theorem. Let's break down the solution step by step.
Step 1: Understand the Initial and Final States
Initially, both the wagon and the pendulum are at rest. The pendulum is deflected at an angle α from the vertical. When the pendulum passes through its mean position, it will have a certain velocity u, and the wagon will have a velocity V.
Step 2: Apply Conservation of Momentum
Since there are no external horizontal forces acting on the system, the horizontal momentum is conserved. Thus, we can write the conservation of momentum equation as:
0=m(−u)+M(V)
Where:
- m is the mass of the pendulum bob,
- u is the velocity of the pendulum bob when it reaches the mean position,
- M is the mass of the wagon,
- V is the velocity of the wagon.
Rearranging gives us:
mu=MV(1)
Step 3: Calculate the Height Change
As the pendulum swings from the angle α to the mean position, it descends a height h. The height h can be calculated using:
h=l(1−cosα)
Where l is the length of the string.
Step 4: Apply the Work-Energy Theorem
The work-energy theorem states that the work done on the system is equal to the change in kinetic energy. The initial kinetic energy is zero since both the wagon and the pendulum are at rest. Thus, we have:
Final Kinetic Energy=Potential Energy lost
The potential energy lost by the pendulum as it descends is:
mgh=mg(l(1−cosα))
The final kinetic energy of the system when the pendulum is at the mean position is:
12mu2+12MV2(2)
Setting the two equal gives us:
12mu2+12MV2=mgl(1−cosα
Step 5: Substitute u from Equation (1) into Equation (2)
From equation (1), we can express u in terms of V:
u=MmV
Substituting this into equation (2):
12m(MmV)2+12MV2=mgl(1−cosα
This simplifies to:
12M2mV2+12MV2=mgl(1−cosα
Step 6: Factor Out V2
Combining the terms gives:
12V2(M2m+M)=mgl(1−cosα
Step 7: Solve for V2
Rearranging gives:
V2=2mgl(1−cosα)M2m+M
Step 8: Take the Square Root to Find V
Finally, we take the square root to find the velocity of the wagon:
V=
⎷2mgl(1−cosα)M2m+M
Summary
The velocity of the wagon when the pendulum passes through its mean position is given by:
V=
⎷2mgl(1−cosα)M2m+M
Initially, both the wagon and the pendulum are at rest. The pendulum is deflected at an angle α from the vertical. When the pendulum passes through its mean position, it will have a certain velocity u, and the wagon will have a velocity V.
Since there are no external horizontal forces acting on the system, the horizontal momentum is conserved. Thus, we can write the conservation of momentum equation as:
- m is the mass of the pendulum bob,
- u is the velocity of the pendulum bob when it reaches the mean position,
- M is the mass of the wagon,
- V is the velocity of the wagon.
As the pendulum swings from the angle α to the mean position, it descends a height h. The height h can be calculated using:
The work-energy theorem states that the work done on the system is equal to the change in kinetic energy. The initial kinetic energy is zero since both the wagon and the pendulum are at rest. Thus, we have:
From equation (1), we can express u in terms of V:
Combining the terms gives:
Rearranging gives:
Finally, we take the square root to find the velocity of the wagon:
⎷2mgl(1−cosα)M2m+M
The velocity of the wagon when the pendulum passes through its mean position is given by:
⎷2mgl(1−cosα)M2m+M
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA pendulum of mass m and length l is suspended from the ceiling of a trolley which has a constant acceleration a in the maximum deflection θ of the pendulum from the vertical.
View SolutionA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a vertical plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the vertical can be
View SolutionA pendulum consisting of a small sphere of mass m, suspended by a inextensible and massless string of length 1 , is made to swing in a verticle plane. If the breaking strength of the string is 2 mg, then the maximum angular amplitude of the displacement from the verticle can be
View SolutionA small metallic sphere of mass m is suspended from the ceiling of a car accelerating on a horizontal road with constant acceleration a. The tension in the string attached with metallic sphere is
View SolutionThe string of pendulum of length l is displaced through 90∘ from the vertical and released. Then the minimum strength of the string in order to withstand the tension, as the pendulum passes through the mean position is
View SolutionA pendulum bob of mass 50 gm is suspended from the ceiling of an elevator. The tension in the string if the elevator goes up with uniform velocity is approximately
View SolutionA simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View Solution
