A wall is inclined to a horizontal surface at an angle of 120∘ as shown. A rod AB of length L=0.75m is sliding with its two ends A and B on the horizontal surface and on the wall respectively. At the moment angle θ=20∘ (see figure), the velocity of end A is vA=1.5 m/s towards right. Calculate the angular speed of the rod at this instant. [Take cos40∘=0.766 ]
![A wall is inclined to a horizontal surface at an angle of 120^(@) as shown. A rod AB of length L = 0.75 m is sliding with its two ends A and B on the horizontal surface and on the wall respectively. At the moment angle theta = 20^(@) (see figure), the velocity of end A is v(A) = 1.5 m/s towards right. Calculate the angular speed of the rod at this instant. [Take cos 40^(@) = 0.766 ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C06_E01_063_Q01.png)
The correct Answer is:2.26 rad/s
Step by step video, text & image solution for A wall is inclined to a horizontal surface at an angle of 120^(@) as shown. A rod AB of length L = 0.75 m is sliding with its two ends A and B on the horizontal surface and on the wall respectively. At the moment angle theta = 20^(@) (see figure), the velocity of end A is v_(A) = 1.5 m/s towards right. Calculate the angular speed of the rod at this instant. [Take cos 40^(@) = 0.766 ] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A rigid rod is rotating as well as translating on a smooth horizontal surface. The velocities of its ends at any moment are as shown in figure. If θ=60∘ find the value of v2
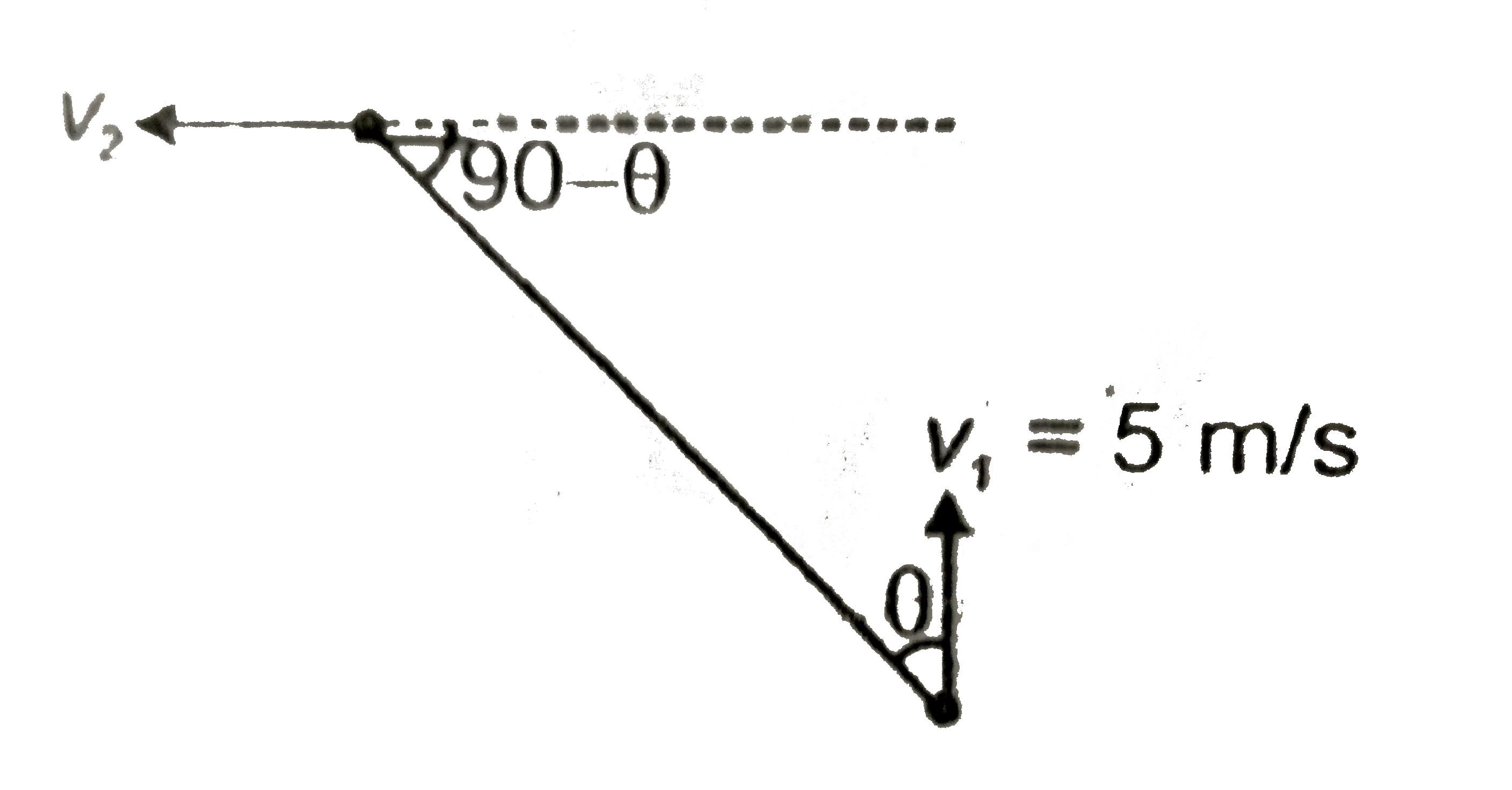
View SolutionA rod AB length 5m which remains in vertical plane has its ends A and B constrained to remain contact with a horizontal floor and a vertical wall respectively. Determine the velocity of the end B and angular velocity at the position shown in Fig. , if the point A has a velocity of 3ms1rightward.

View Solution
Knowledge Check
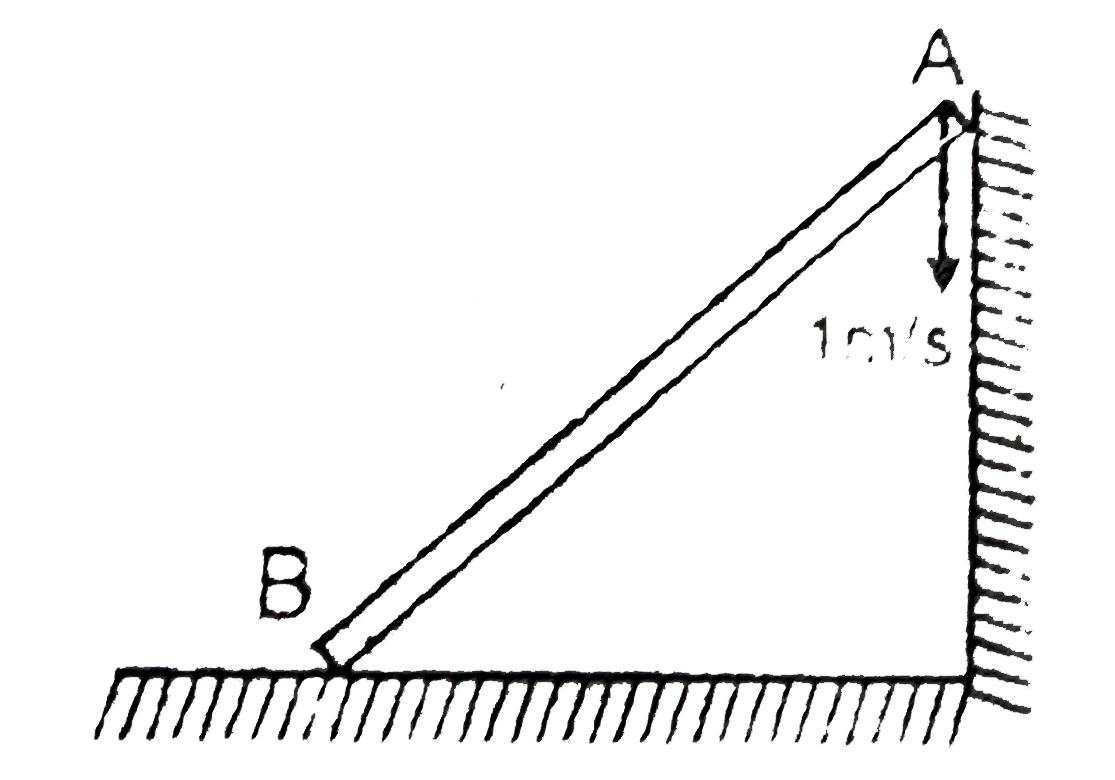
A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
 A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
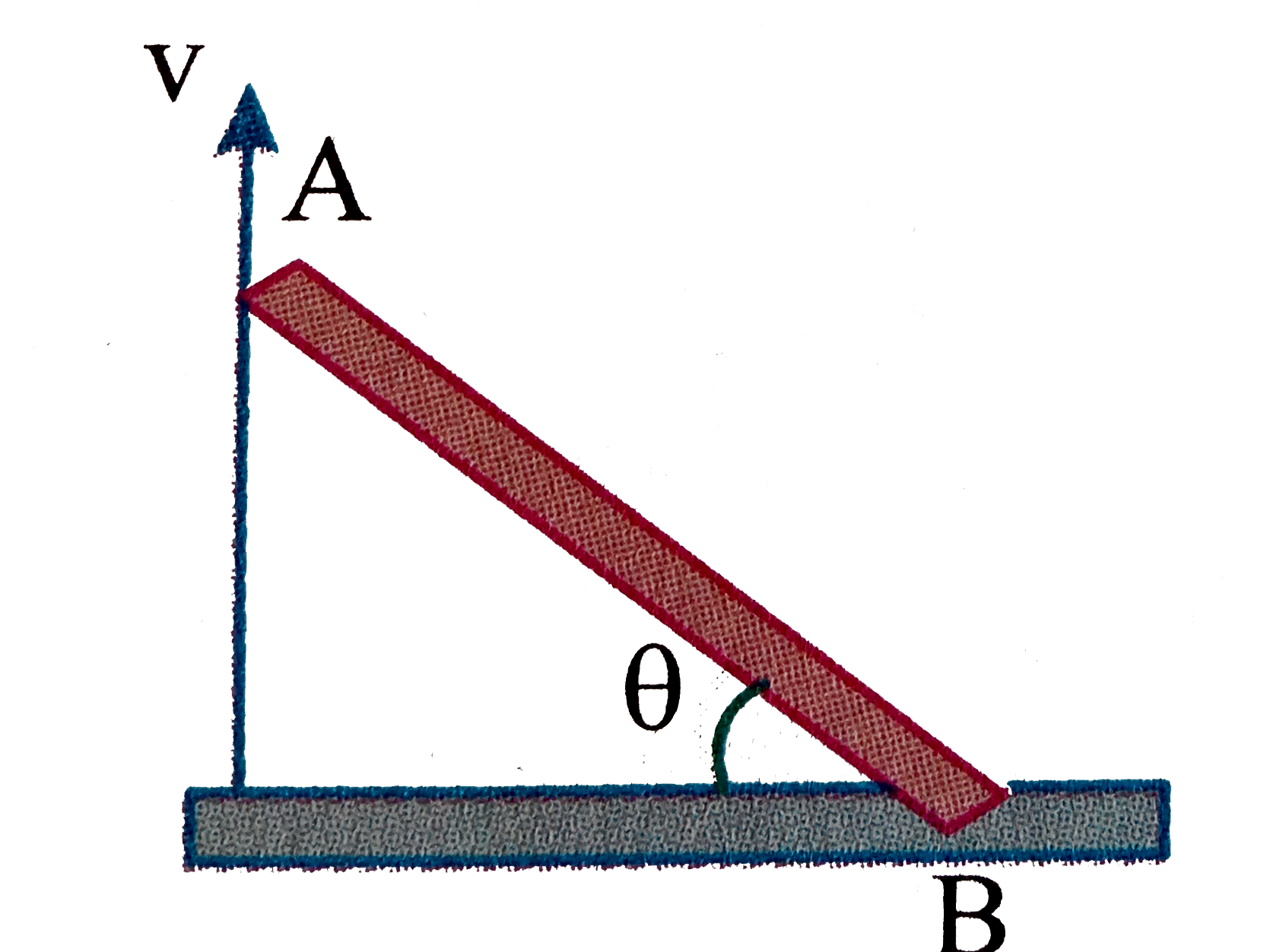
A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/sPoint A of rod AB(l=2m) is moved upwards against a wall with velocity v=2m/s. Find angular speed of the rod at an instant when θ=60∘.
 A4rad/sB1.155rad/sC2rad/sD2.50rad/s
A4rad/sB1.155rad/sC2rad/sD2.50rad/sIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of these
A rod length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At a certain instant of time, when the rod makes an angle θ with horizontal the velocity of COM of the rod is v0. The velocity of the end of the rod in contact with the surface at that instant is:
View SolutionA rod of length L is held vertically on a smooth horizontal surface. The top end of the rod is given a gentle push. At at certain instant of time, when the rod makes an angle 37∘ with horizontal the velocity of COM of the rod of 2m/s. The velocity of the end of the rod in contact with the surface at that instant is
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View SolutionA ladder of length L is slipping with its ends against a vertical wall and a horizontal floor. At a certain moment, the speed of the end in contact with the horizontal floor is v and the ladder makes an angle θ=30∘ with horizontal. Then, the speed of the ladder's centre of mass must be
View SolutionA uniform rod of length 2l is placed with one end in contact with the horizontal table and is then inclined at an angle α to the horizontal and allowed to fall. When it becomes horizontal, its angular velocity will be
View Solution
