A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
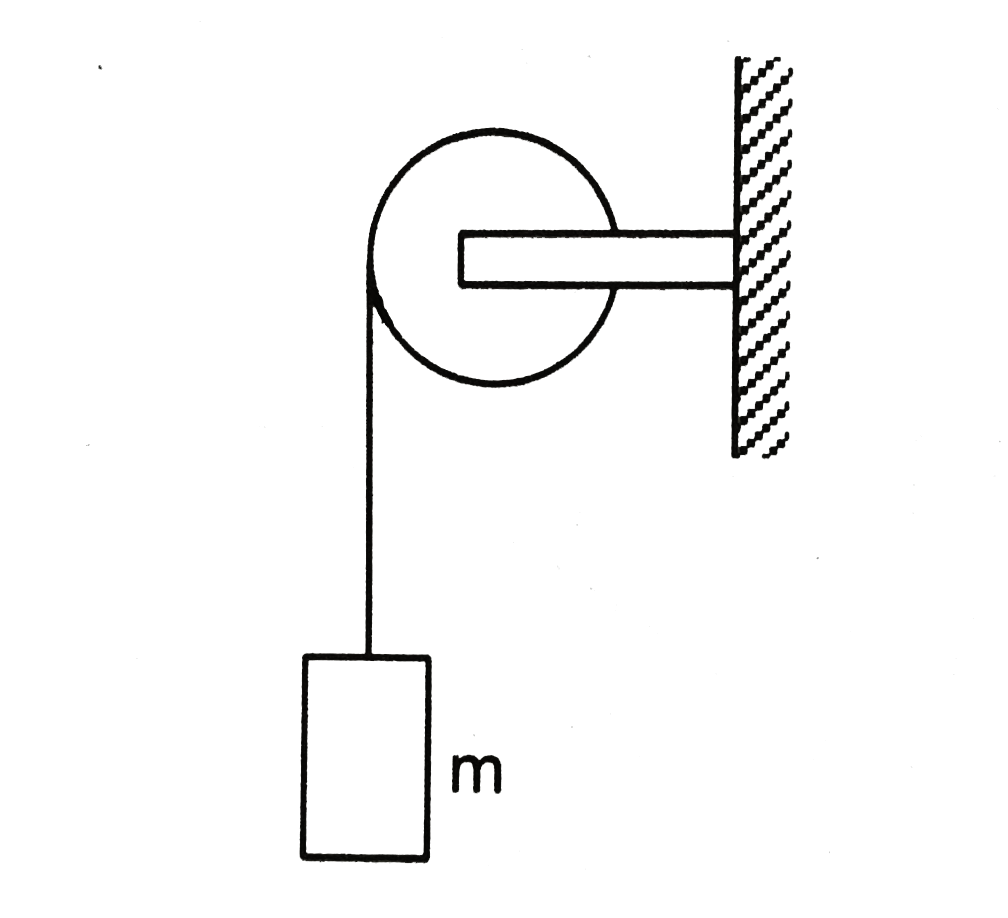
Let the speed of the block be v when it descends thrugha height h. Sol is the speed of the string and hence of a particle at the rim of the wheel. The angular velocity of the wheel is vr and it skinetic energy at this instant is 12I(vr)2. Using the prnciple of conservation of energy the gragvitastioN/Al potential energy lost by the block must be equal to the kinetic energy gained by the block and the wheel. Thus,
mgh−12mv2+12Iv2r2
orv=⎡⎢⎣2mghm+Ir2⎤⎥⎦12
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
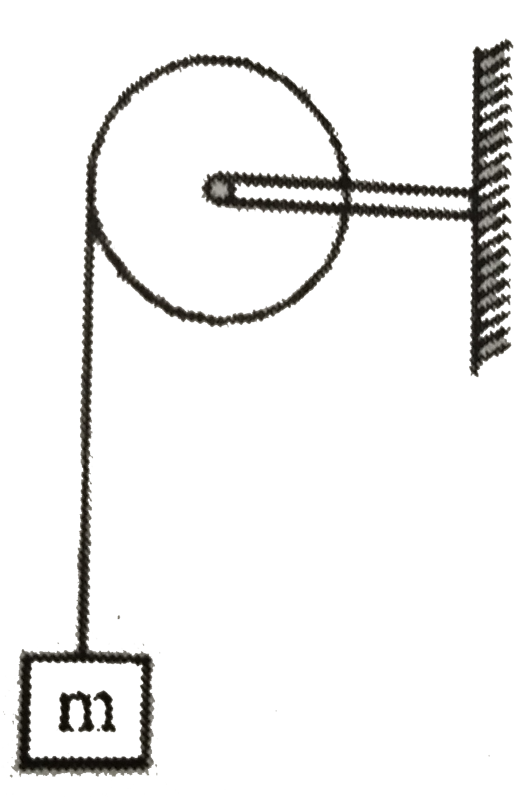
A disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
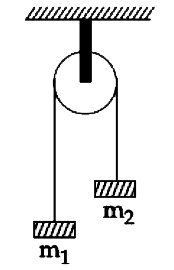
View SolutionA uniformly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses m1andm2(m1>m2) are attached to the ends of the string. The system is released from rest. The angular speed of the wheel when m1 descents by a distance h is :
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
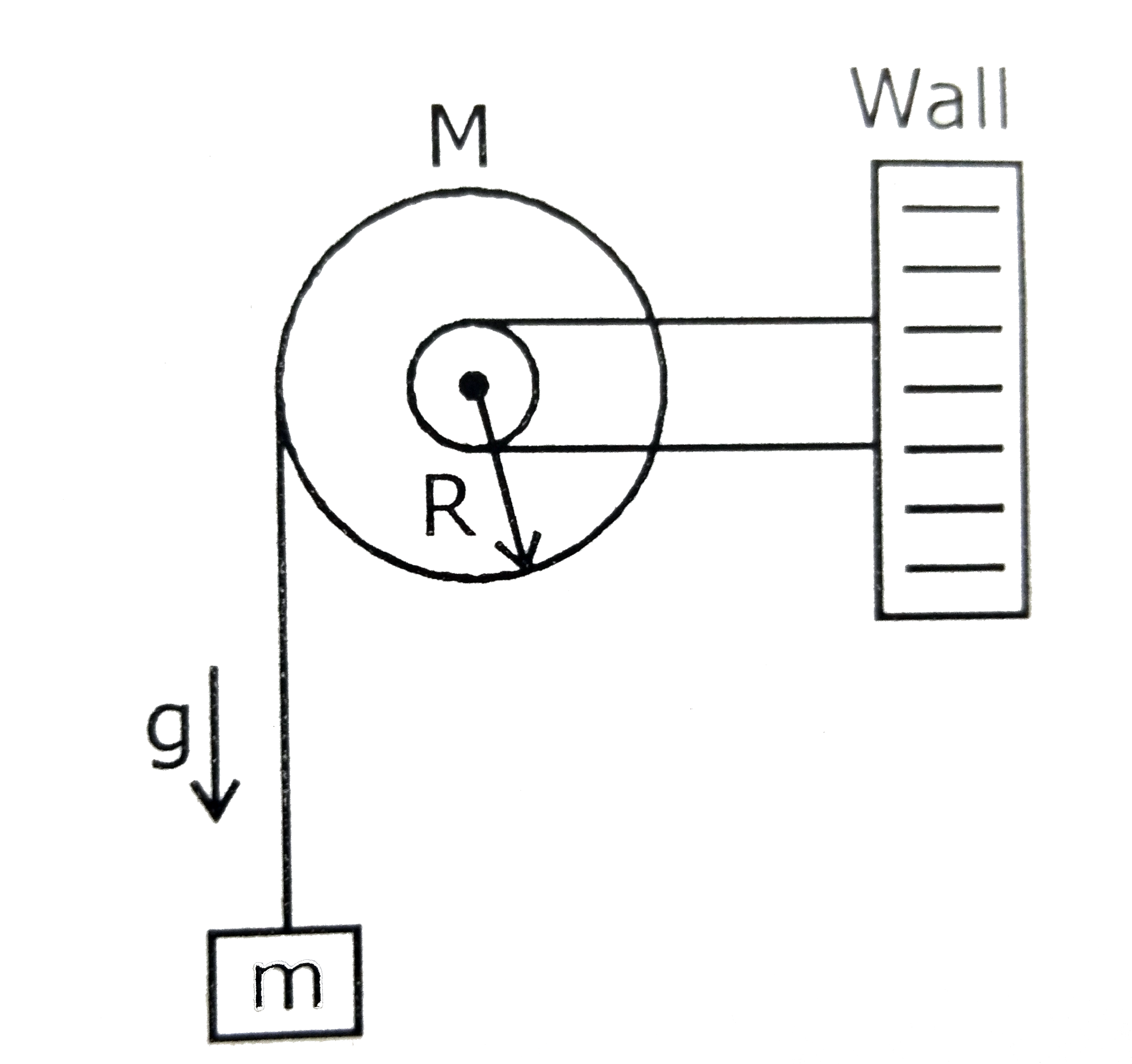
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is

View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View SolutionA wheel of moment of inertia I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.

View SolutionFor given system as shown in figure, the acceleration of block of mass m(m=M/2) kept on smooth table when the system is released from rest is (Strings and pulleys are ideal)
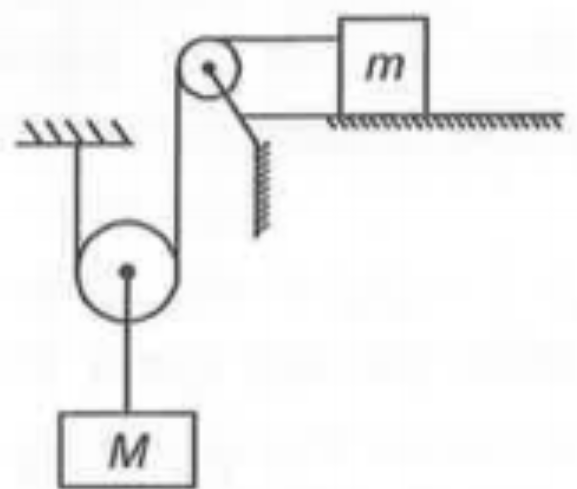
View Solution
