If several forces act on a particle, the total torque on the particle mauy be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces actin on difeent partivles of a body in such a way that their lines of acting intersect at a common point?
To prove that the total torque on a particle due to several forces can be obtained by first finding the resultant force and then taking the torque of this resultant, we can follow these steps:
Step 1: Define Torque
Torque (τ) is defined as the cross product of the position vector (r) and the force vector (F):
τ=r×F
where r is the position vector from the axis of rotation to the point where the force is applied.
Step 2: Consider Multiple Forces
Let’s consider several forces F1,F2,…,Fn acting on a particle at point P. The torque due to each force can be expressed as:
τ1=r×F1,τ2=r×F2,…,τn=r×Fn
Step 3: Calculate Total Torque
The total torque (τtotal) due to all the forces acting on the particle is the vector sum of the individual torques:
τtotal=τ1+τ2+…+τn=r×F1+r×F2+…+r×Fn
Step 4: Factor Out the Position Vector
Using the distributive property of the cross product, we can factor out the position vector r:
τtotal=r×(F1+F2+…+Fn)
Step 5: Define Resultant Force
Let Fresultant be the resultant force of all the forces acting on the particle:
Fresultant=F1+F2+…+Fn
Step 6: Express Total Torque in Terms of Resultant Force
Substituting the resultant force into the equation for total torque gives:
τtotal=r×Fresultant
This shows that the total torque can indeed be obtained by first finding the resultant force and then taking the torque of this resultant.
Step 7: Consider Forces Acting on Different Particles
Now, we need to consider if this result is valid for forces acting on different particles of a body whose lines of action intersect at a common point.
If the lines of action of all forces intersect at a common point P, we can shift the lines of action to point P without changing the torque about that point. This is because the torque depends on the perpendicular distance from the axis of rotation to the line of action of the force.
Conclusion
Thus, if the lines of action of the forces intersect at a common point, we can treat them as if they are acting at that point, and the resultant torque can still be calculated using the resultant force.
Torque (τ) is defined as the cross product of the position vector (r) and the force vector (F):
τ=r×F
where r is the position vector from the axis of rotation to the point where the force is applied.
Let’s consider several forces F1,F2,…,Fn acting on a particle at point P. The torque due to each force can be expressed as:
τ1=r×F1,τ2=r×F2,…,τn=r×Fn
The total torque (τtotal) due to all the forces acting on the particle is the vector sum of the individual torques:
τtotal=τ1+τ2+…+τn=r×F1+r×F2+…+r×Fn
Using the distributive property of the cross product, we can factor out the position vector r:
τtotal=r×(F1+F2+…+Fn)
Let Fresultant be the resultant force of all the forces acting on the particle:
Fresultant=F1+F2+…+Fn
Substituting the resultant force into the equation for total torque gives:
τtotal=r×Fresultant
This shows that the total torque can indeed be obtained by first finding the resultant force and then taking the torque of this resultant.
Now, we need to consider if this result is valid for forces acting on different particles of a body whose lines of action intersect at a common point.
Thus, if the lines of action of the forces intersect at a common point, we can treat them as if they are acting at that point, and the resultant torque can still be calculated using the resultant force.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
Knowledge Check
Let →F be a force acting on a particle having positon vector →r.Let→τ be the torque of this force about the origin then
A→r.→τ>0 and →F.→τ<0B→r.→τ=0 and →F.→τ=0C→r.→τ=0 and →F.→τ≠0D→r.→τ≠0 and →F.→τ=0
If the resultant torque of all the forces acting on a body is zero about a point is it necessary that it will be zero about any other point?
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
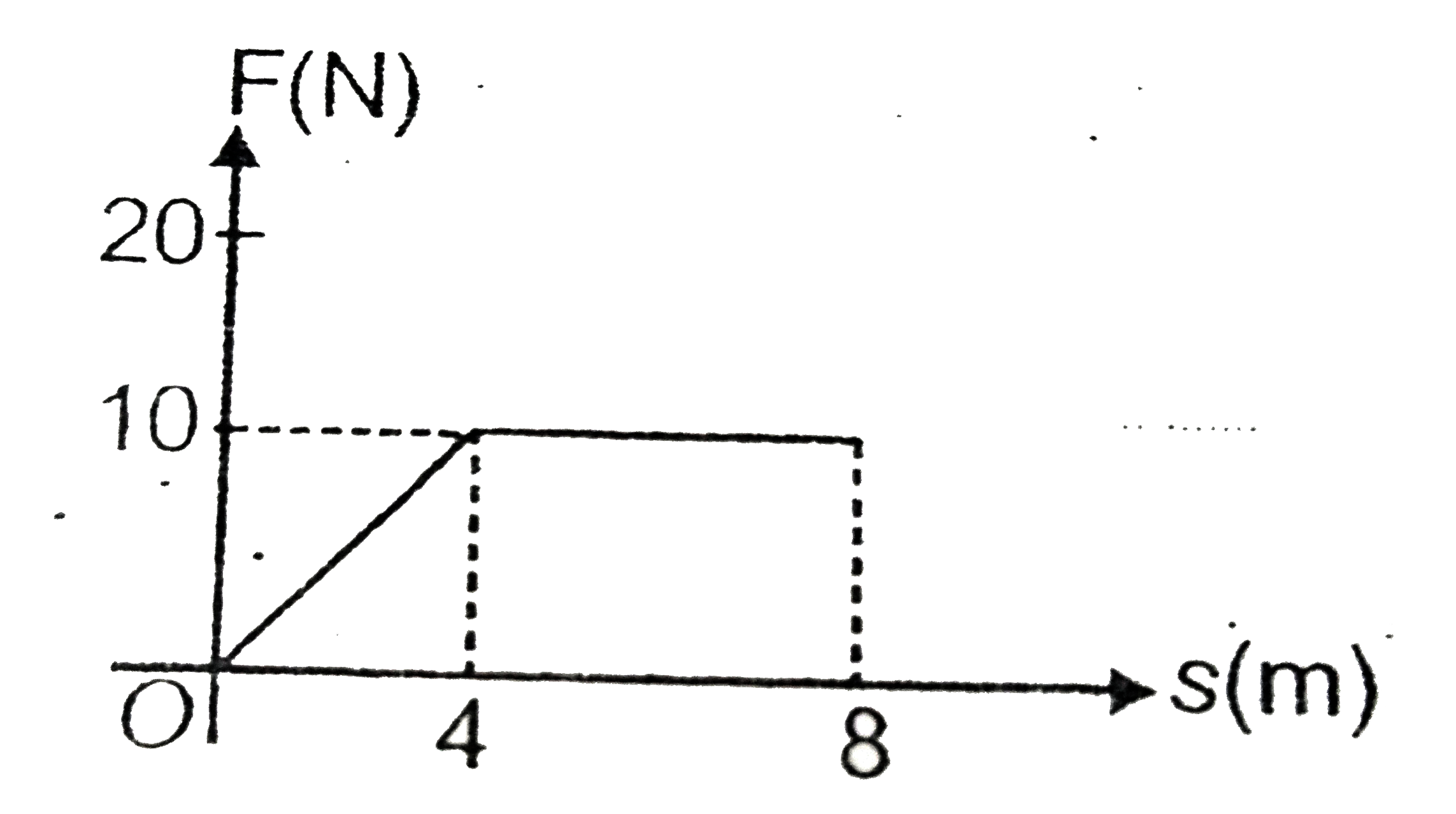
View SolutionIf the resultant of n forces of different magnitudes acting at a point is zero, then the minimum value of n is
View SolutionTwo forces, while acting on particle in opposite directions,have the resultant of 10N. If they act at right angles to each other, the resultant is found to be 50N. Find the two forces?
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionTwo forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
View SolutionLet →F be the force acting on a particle having position vector →rand→T be the torque of this force about the origin. Then
View Solution

