If the angular momentum of a body is found to be zero about a point is it necessary that it will also be zero about a different point?
To determine whether the angular momentum of a body being zero about one point implies it will also be zero about a different point, we can analyze the situation using the definition of angular momentum.
1. Understanding Angular Momentum:
The angular momentum L of a particle about a point is given by the formula:
L=r×p
where r is the position vector from the point to the particle, and p=mv is the linear momentum of the particle (with m being the mass and v the velocity).
2. Condition for Zero Angular Momentum:
For the angular momentum to be zero about a point, the cross product r×p must be zero. This can happen in two scenarios:
- The position vector r is zero (i.e., the particle is located at the point).
- The vectors r and p are parallel (i.e., the angle θ between them is 0 or 180 degrees).
3. Considering a Different Point:
If we consider a different point O′ and calculate the angular momentum about this new point, the position vector r′ will generally be different from r. Therefore, the angular momentum about point O′ can be expressed as:
L′=r′×p
4. Dependence on Position Vector:
Since the position vector r changes when we switch points, the angular momentum L is dependent on the position vector. Thus, even if the angular momentum is zero about one point, it does not guarantee that it will be zero about another point.
5. Conclusion:
Therefore, it is not necessary that the angular momentum will also be zero about a different point. The angular momentum can be non-zero depending on the position vector relative to the new point.
Final Answer:
No, it is not necessary that the angular momentum will also be zero about a different point.
The angular momentum L of a particle about a point is given by the formula:
L=r×p
where r is the position vector from the point to the particle, and p=mv is the linear momentum of the particle (with m being the mass and v the velocity).
For the angular momentum to be zero about a point, the cross product r×p must be zero. This can happen in two scenarios:
- The position vector r is zero (i.e., the particle is located at the point).
- The vectors r and p are parallel (i.e., the angle θ between them is 0 or 180 degrees).
If we consider a different point O′ and calculate the angular momentum about this new point, the position vector r′ will generally be different from r. Therefore, the angular momentum about point O′ can be expressed as:
L′=r′×p
Since the position vector r changes when we switch points, the angular momentum L is dependent on the position vector. Thus, even if the angular momentum is zero about one point, it does not guarantee that it will be zero about another point.
Therefore, it is not necessary that the angular momentum will also be zero about a different point. The angular momentum can be non-zero depending on the position vector relative to the new point.
No, it is not necessary that the angular momentum will also be zero about a different point.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
If the angular momentum of a body is zero about some point. Is it necessary that it will be zero. About a differet point?
View SolutionIf the resultant torque of all the forces acting on a body is zero about a point is it necessary that it will be zero about any other point?
View SolutionA body is in translational equilibrium under the sctin of coplanar forces. If the torque of these force is zero about a point is it necessary that it will also be zero abut any other point?
View Solution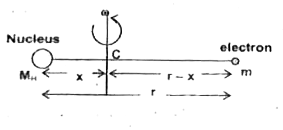
The angular momentum of the atom about the centre of mass will be
View SolutionAngular momentum of a planet about the point of it's apogee is
View Solution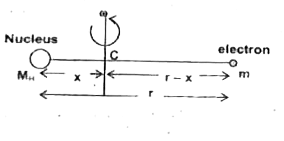
The angular momentum of the atom will be constant about an axis passing through
View SolutionThe angular momentum of an electron is zero. In which orbital may it be present?
View SolutionA : If angular momentum of an object is constant about a point then net torque on it about that point is zero.
R : Torque is equal to the rate of change of angular momentum.
View SolutionIf angular momentum of a system is constant, which of the following will be zero
View SolutionAngular momentum of a rigid body rotating about a fixed Axis with angular velocity →ω
View Solution
