In a rotating body a=αrandv=ωr. Thus aα=vω. Can you use the theorems of ratio and proportion studied in algebra so as to write
a+αa−α=v+ωv−ω
To solve the question, we need to analyze the relationships between the quantities involved and determine whether we can apply theorems of ratio and proportion to the given expressions.
1. Understanding the Given Relationships:
- We know that for a rotating body, the linear acceleration a is related to angular acceleration α by the formula:
a=αr
- Similarly, the linear velocity v is related to angular velocity ω by:
v=ωr
2. Establishing the Ratio:
- From the above equations, we can derive the ratio:
aα=randvω=r
- This implies that:
aα=vω
3. Analyzing the Proposed Expression:
- The question asks if we can write:
a+αa−α=v+ωv−ω
- To do this, we need to check if we can add and subtract the quantities a and α, and v and ω.
4. Checking Units:
- The unit of linear acceleration a is m/s2.
- The unit of angular acceleration α is rad/s2.
- Since a and α have different units, we cannot directly add or subtract them.
- The same reasoning applies to v and ω:
- The unit of linear velocity v is m/s.
- The unit of angular velocity ω is rad/s.
- Again, v and ω have different units, making it impossible to add or subtract them directly.
5. Conclusion:
- Since we cannot add or subtract quantities with different units, we cannot use theorems of ratio and proportion to write the expression:
a+αa−α=v+ωv−ω
- Therefore, the answer is No, we cannot write this expression.
- We know that for a rotating body, the linear acceleration a is related to angular acceleration α by the formula:
a=αr
- Similarly, the linear velocity v is related to angular velocity ω by:
v=ωr
- From the above equations, we can derive the ratio:
aα=randvω=r
- This implies that:
aα=vω
- The question asks if we can write:
a+αa−α=v+ωv−ω
- To do this, we need to check if we can add and subtract the quantities a and α, and v and ω.
- The unit of linear acceleration a is m/s2.
- The unit of angular acceleration α is rad/s2.
- Since a and α have different units, we cannot directly add or subtract them.
- The same reasoning applies to v and ω:
- The unit of linear velocity v is m/s.
- The unit of angular velocity ω is rad/s.
- Again, v and ω have different units, making it impossible to add or subtract them directly.
- Since we cannot add or subtract quantities with different units, we cannot use theorems of ratio and proportion to write the expression:
a+αa−α=v+ωv−ω
- Therefore, the answer is No, we cannot write this expression.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
If I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
View SolutionIf a ,b,c, and u,v,w are complex numbers representing the vertices of two triangle such that they are similar, then prove that a−ca−b=u−wu−v
View SolutionIn figure, if the current i decreases at a rate α then VA−VB is

View SolutionA body is in pure rotation. The linear speed 'v' of a particle, the distance 'r' of the particle from the axis and the angular velocity ω of the body are related as ω=vr. Thus
View SolutionFor a particle of a rotating rigid body, v=rω, which of the following are correct ?
View SolutionA proton a deutron and an α particle are accelerated through potentials of V,2V and 4V respectively. Their velocity will bear a ratio
View SolutionA proton a deutron and an α particle are accelerated through potentials of V,2V and 4V respectively. Their velocity will bear a ratio
View SolutionIn the circuit given in fig. (VC)=50VandR=50Ω. The values of C and (VR) are
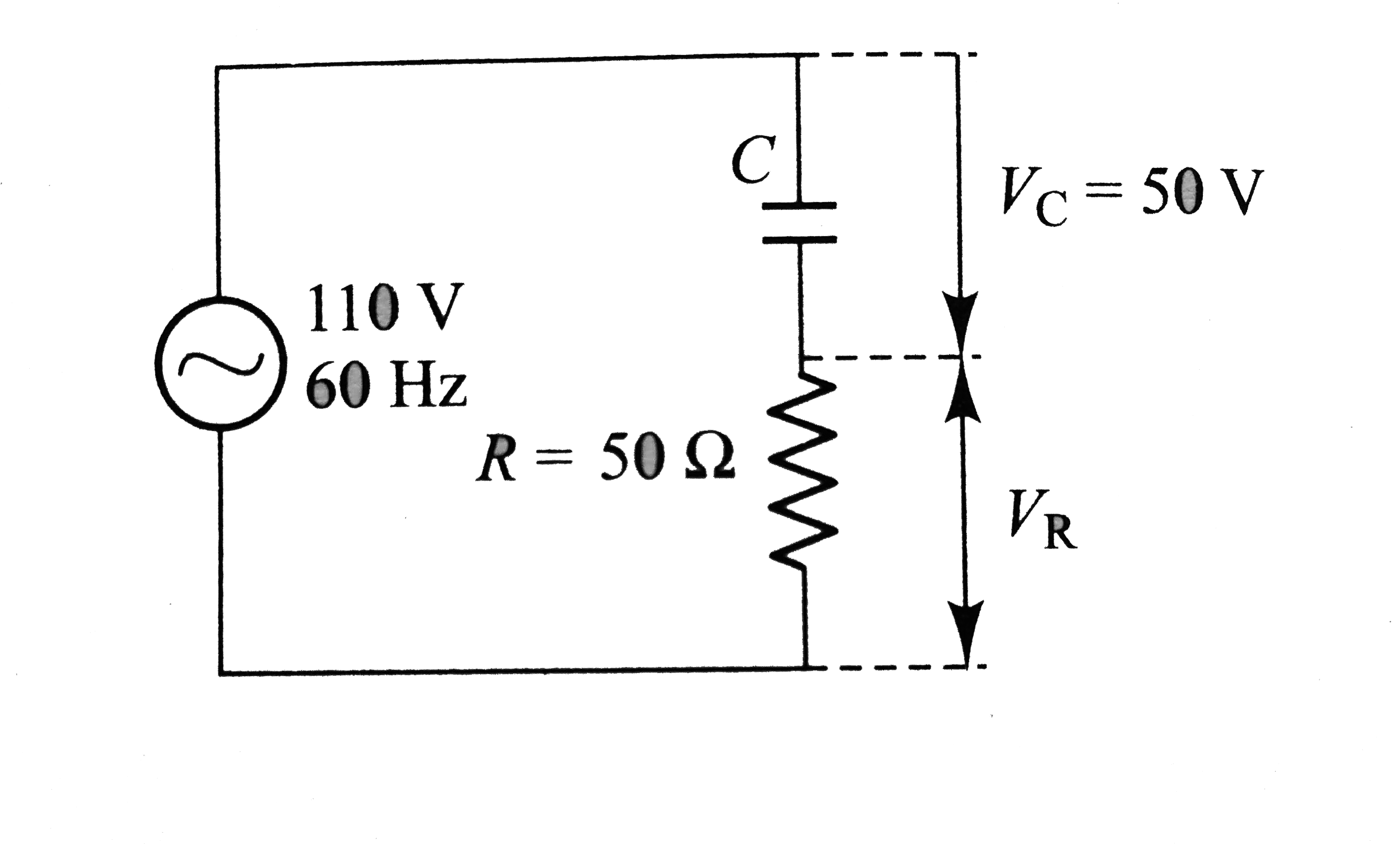
View SolutionIn the following reaction, sequences V and W are respectively.

View SolutionA particle is projected in gravity with a speed v0. Using W-E theorem, find the speed of the particle as the function of vertical distance y.
View Solution
