A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
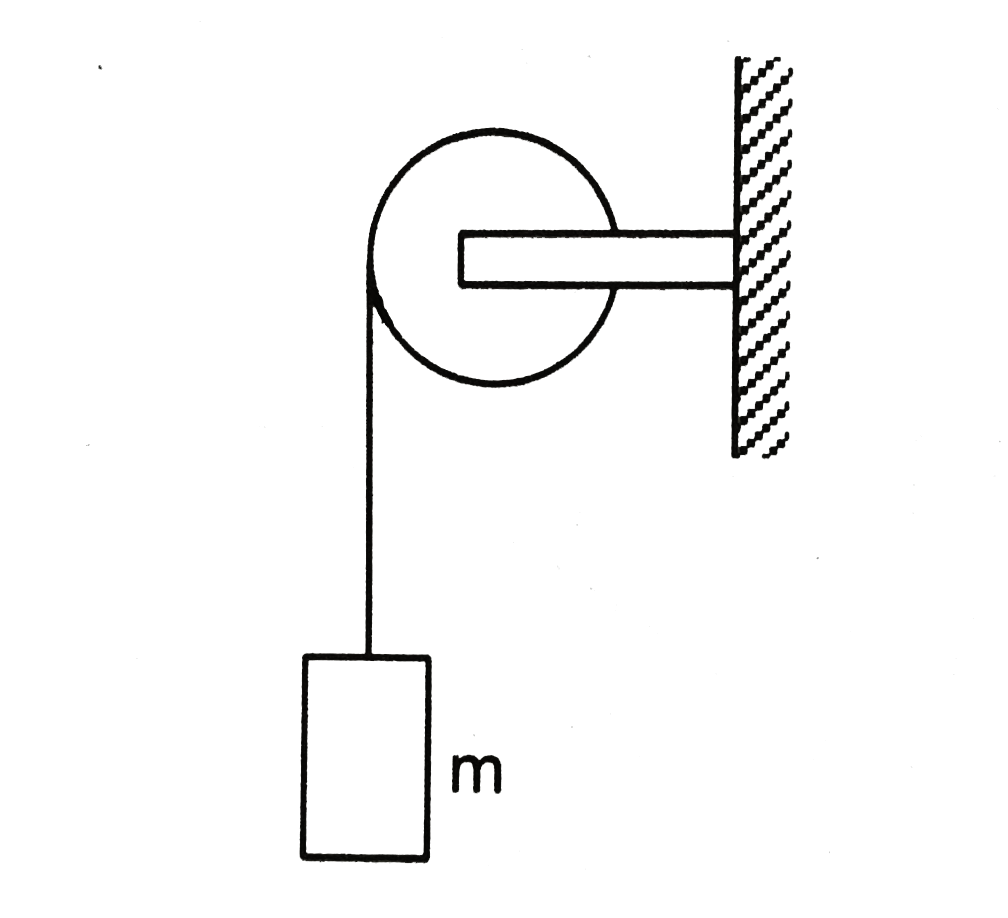 Solution in Tamil
Solution in Tamil
Let the speed of the block be v when it descends thrugha height h. Sol is the speed of the string and hence of a particle at the rim of the wheel. The angular velocity of the wheel is vr and it skinetic energy at this instant is 12I(vr)2. Using the prnciple of conservation of energy the gragvitastioN/Al potential energy lost by the block must be equal to the kinetic energy gained by the block and the wheel. Thus,
mgh−12mv2+12Iv2r2
orv=⎡⎢⎣2mghm+Ir2⎤⎥⎦12
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
22 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A wheel rotates with a constant acceleration of 2.0rads2. If the wheel starts from rest, how many revolutions will it make in the first 10 seconds?
View SolutionCan an object be in pure translation as well as in pure rotation?
View SolutionA man goes 10 m due east and then 24 m due north. Find the distance of his current position from the starting point ?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
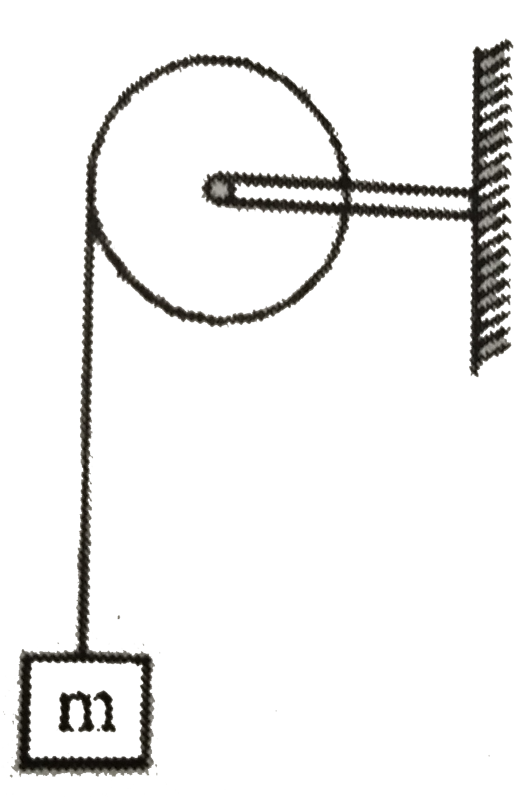
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
View SolutionA uniformaly thick wheel with moment of inertia I and radius R is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses m_(1)an d m_(2)(m_(1)gtm_(2)) are attached to the ends of the strung. The system is released from rest. The angular speed of the wheel when m_(1) descents by a distance h is :
View SolutionA wheel whose radius is R and moment of inertia about its own axis is I, rotates freely about its own axis. A rope is wrapped on the wheel. A body of mass m is suspended from the free end of the rope. The body is released from rest. The velocity of the body after falling a distance h would be:
View SolutionIn the system shown in figure, the block A is released from rest. Find
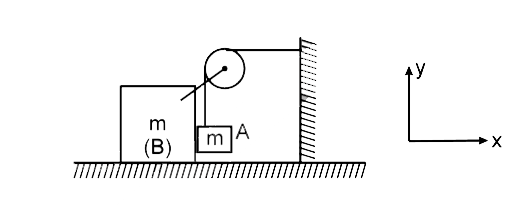
Tension in the string.
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View SolutionTwo' blocks of masses m, and m, are connected to the two ends of a string passing over a pulley as shown in figure. System hans vertically and blocks are held at rest. Assume that m_(1) gt m_(2) . Find the speed attained by the blocks when m, descends through a height h. Moment of inertia of the pulley is I and its radius is r. There is enough friction between string and pulley so that there is no slipping between them.
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
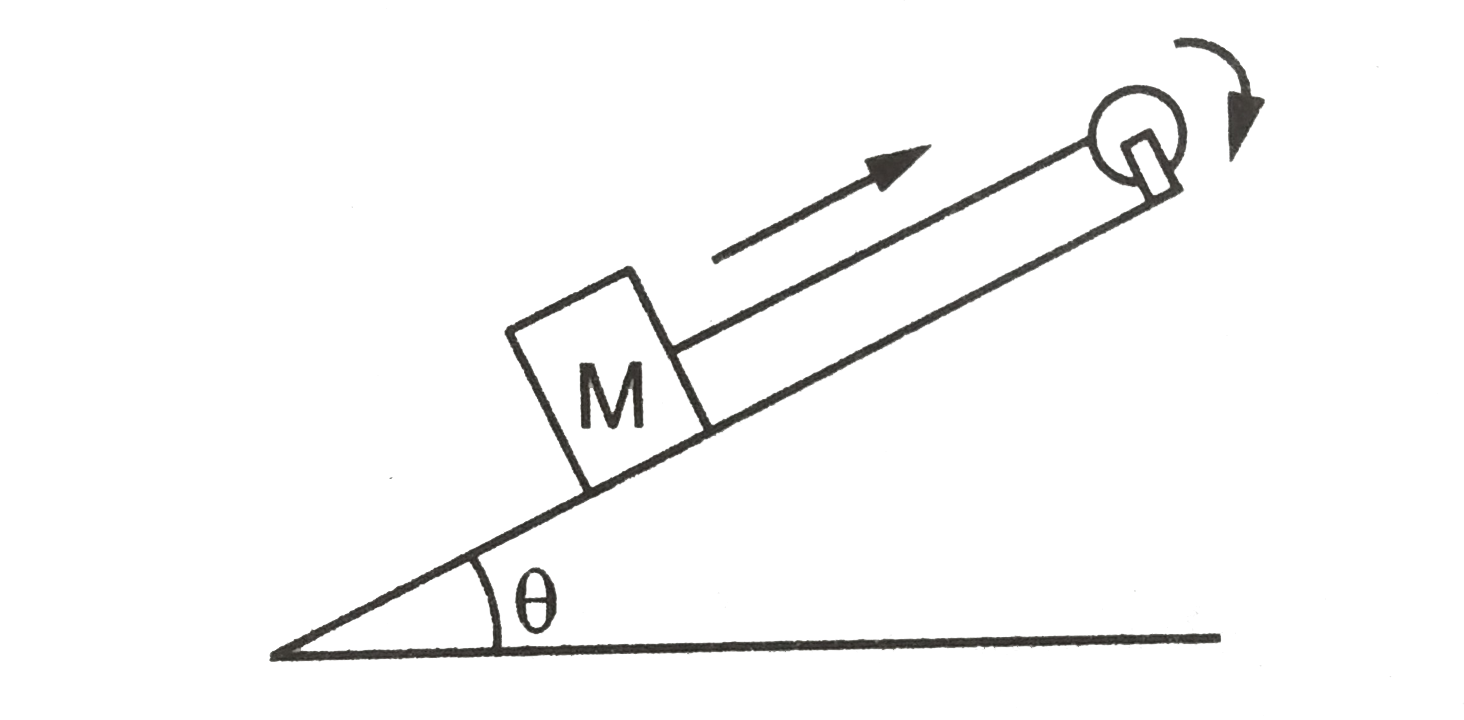
View SolutionA wheel of radius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shown in figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. Initially, the wheel is rotating at a speed ω in direction such that the block slides up the plane. How far will the block move before stopping?
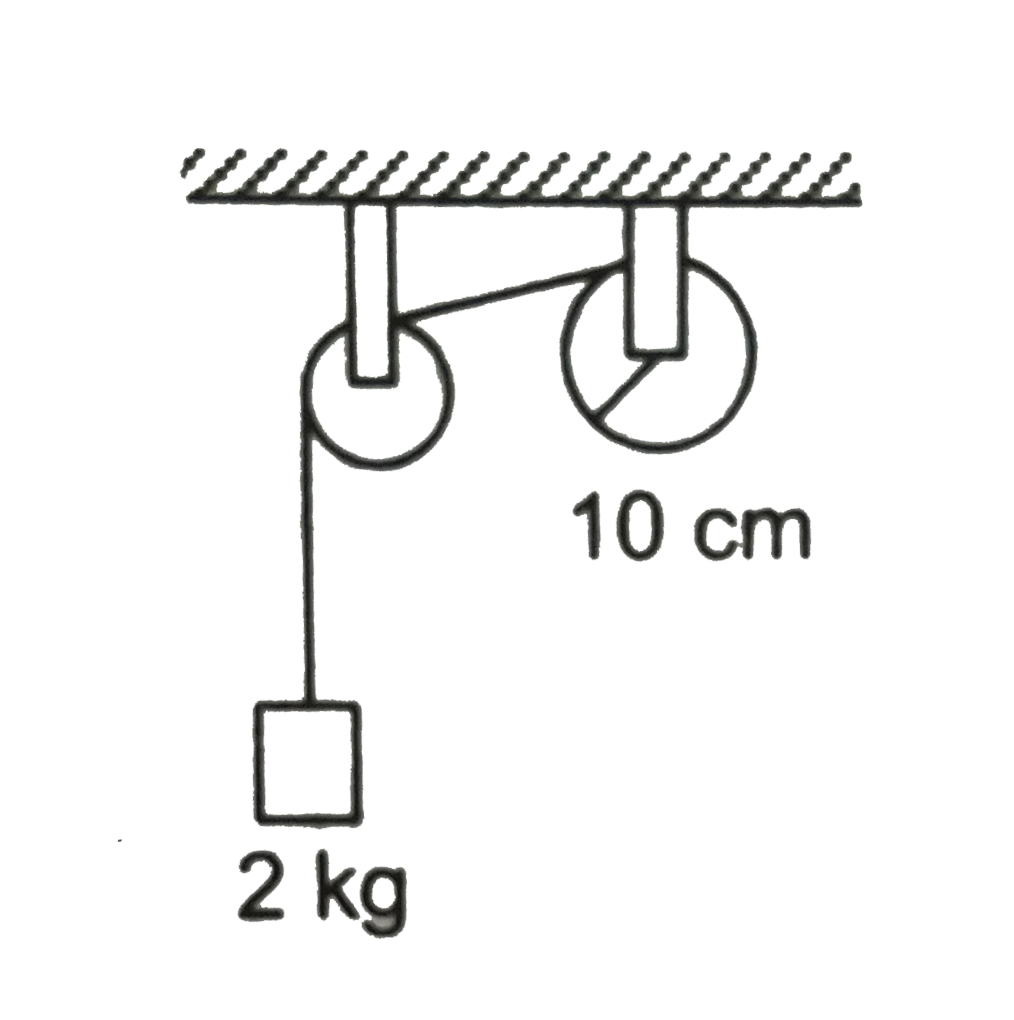
View SolutionA string is wrapped on a wheel of moment of inertia 0.20 kg-m^2 and radius 10 cm and goes through a light pulley to support a block of mass 2.0 kg as shown in figure. Find the acceleration of the block.
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
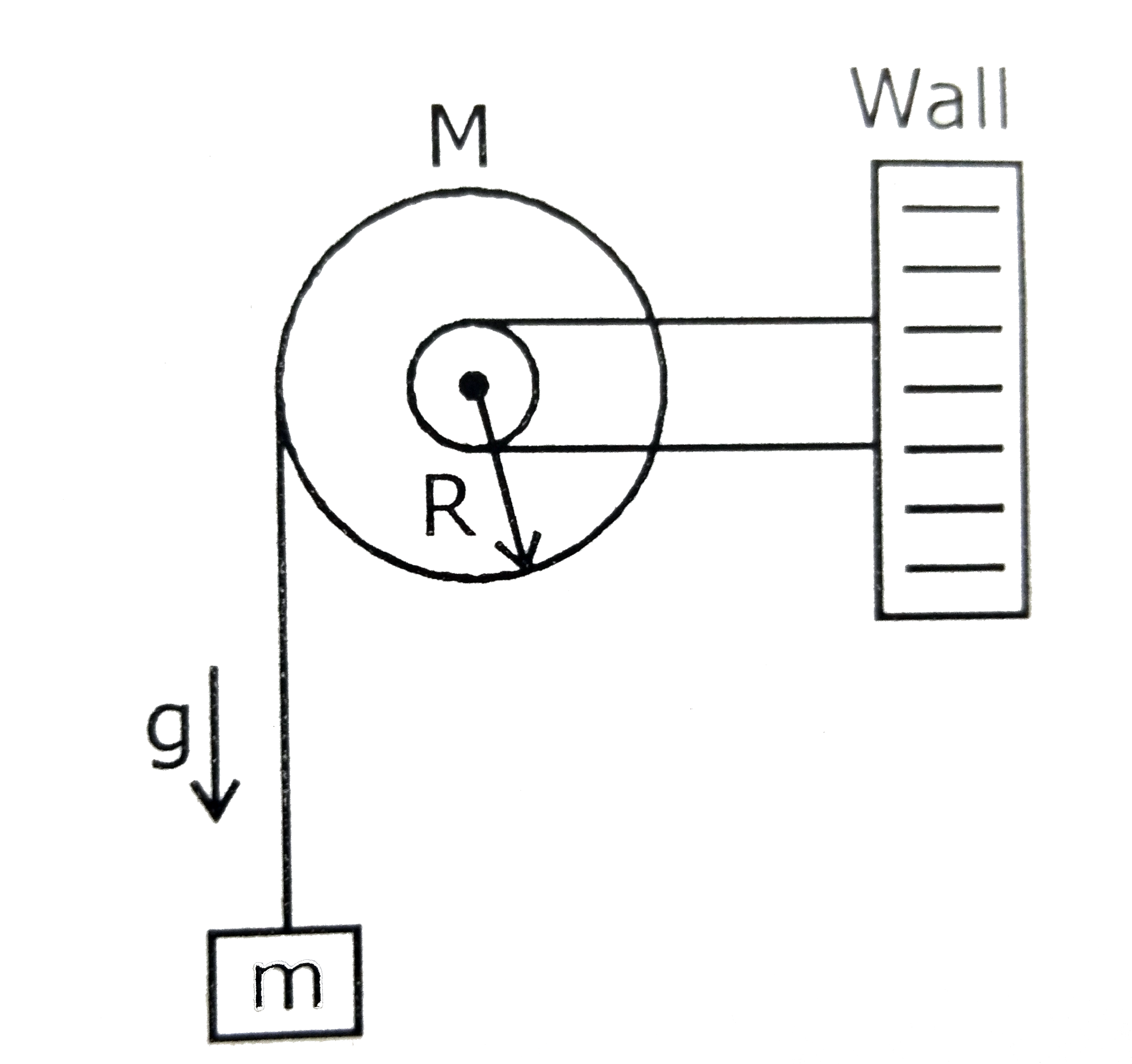
View SolutionA uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
View Solution
