A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
To find the electric field at the center of a regular hexagon with a total charge q uniformly distributed along its sides, we can follow these steps:
Step 1: Understand the Geometry
A regular hexagon has six equal sides and is symmetric about its center. The center of the hexagon is equidistant from all its vertices.
Hint: Visualize the hexagon and its symmetry. Each side contributes to the electric field at the center.
Step 2: Consider the Charge Distribution
The charge q is uniformly distributed along the six sides of the hexagon. Because of the symmetry of the hexagon, each side will contribute equally to the electric field at the center.
Hint: Think about how the electric field from each side behaves due to symmetry.
Step 3: Analyze the Electric Field Contribution
For any small charge element dq on one side of the hexagon, there will be an equal and opposite charge element dq′ on the side directly opposite to it. The electric field produced by dq at the center will have a certain direction, and the electric field produced by dq′ will point in the opposite direction.
Hint: Consider the direction of the electric field vectors from opposite sides.
Step 4: Sum the Electric Fields
When you sum the electric field contributions from all six sides, the fields from opposite sides will cancel each other out due to their equal magnitude and opposite direction.
Hint: Use vector addition to see how the electric fields from opposite sides cancel.
Step 5: Conclude the Result
Since the contributions from all sides cancel out, the net electric field at the center of the hexagon is zero.
Hint: Reflect on the concept of symmetry and cancellation in electric fields.
Final Answer
The electric field at the center of the hexagon is E=0.
A regular hexagon has six equal sides and is symmetric about its center. The center of the hexagon is equidistant from all its vertices.
The charge q is uniformly distributed along the six sides of the hexagon. Because of the symmetry of the hexagon, each side will contribute equally to the electric field at the center.
For any small charge element dq on one side of the hexagon, there will be an equal and opposite charge element dq′ on the side directly opposite to it. The electric field produced by dq at the center will have a certain direction, and the electric field produced by dq′ will point in the opposite direction.
When you sum the electric field contributions from all six sides, the fields from opposite sides will cancel each other out due to their equal magnitude and opposite direction.
Since the contributions from all sides cancel out, the net electric field at the center of the hexagon is zero.
The electric field at the center of the hexagon is E=0.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples
19 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is

View SolutionA charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
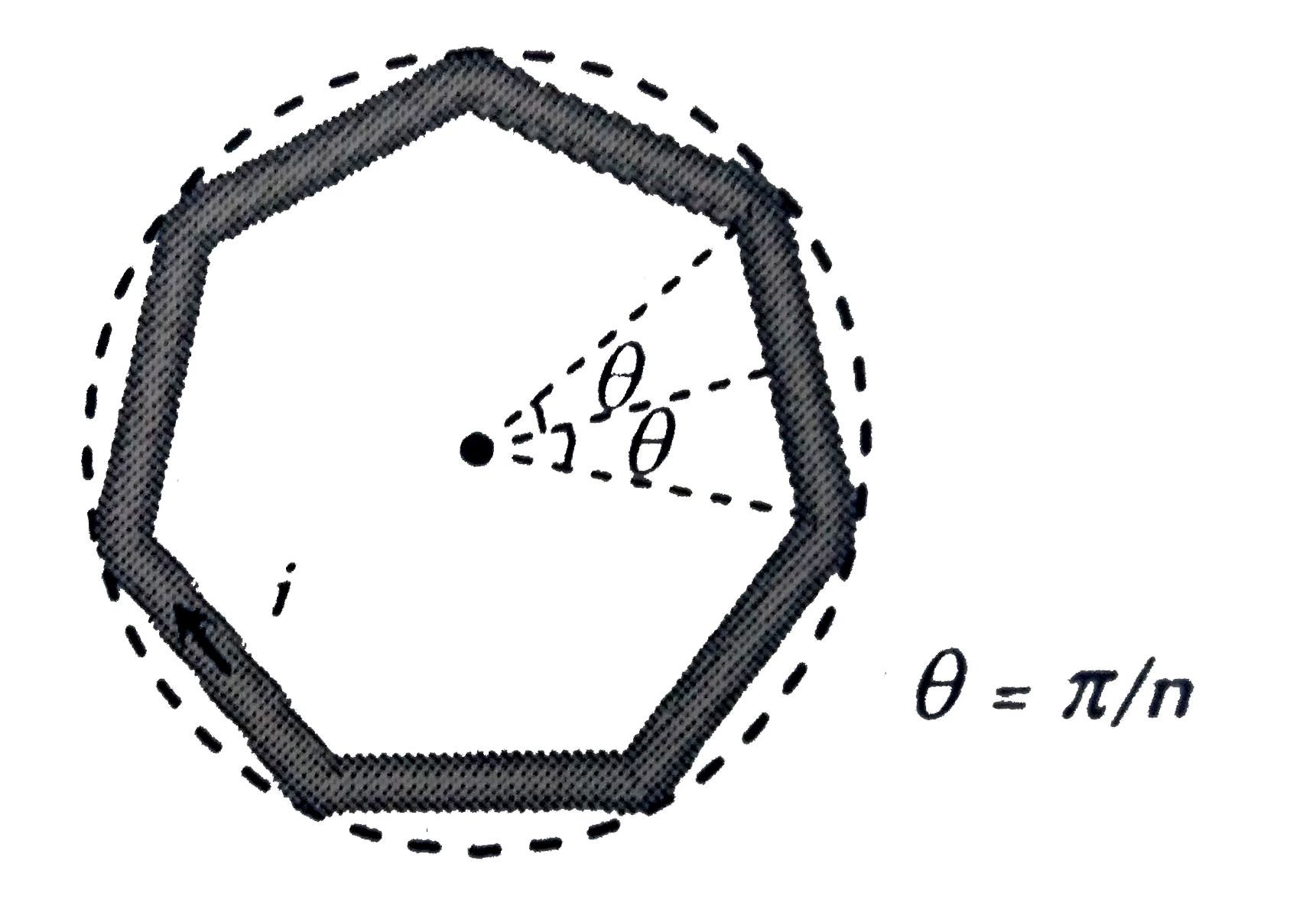
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
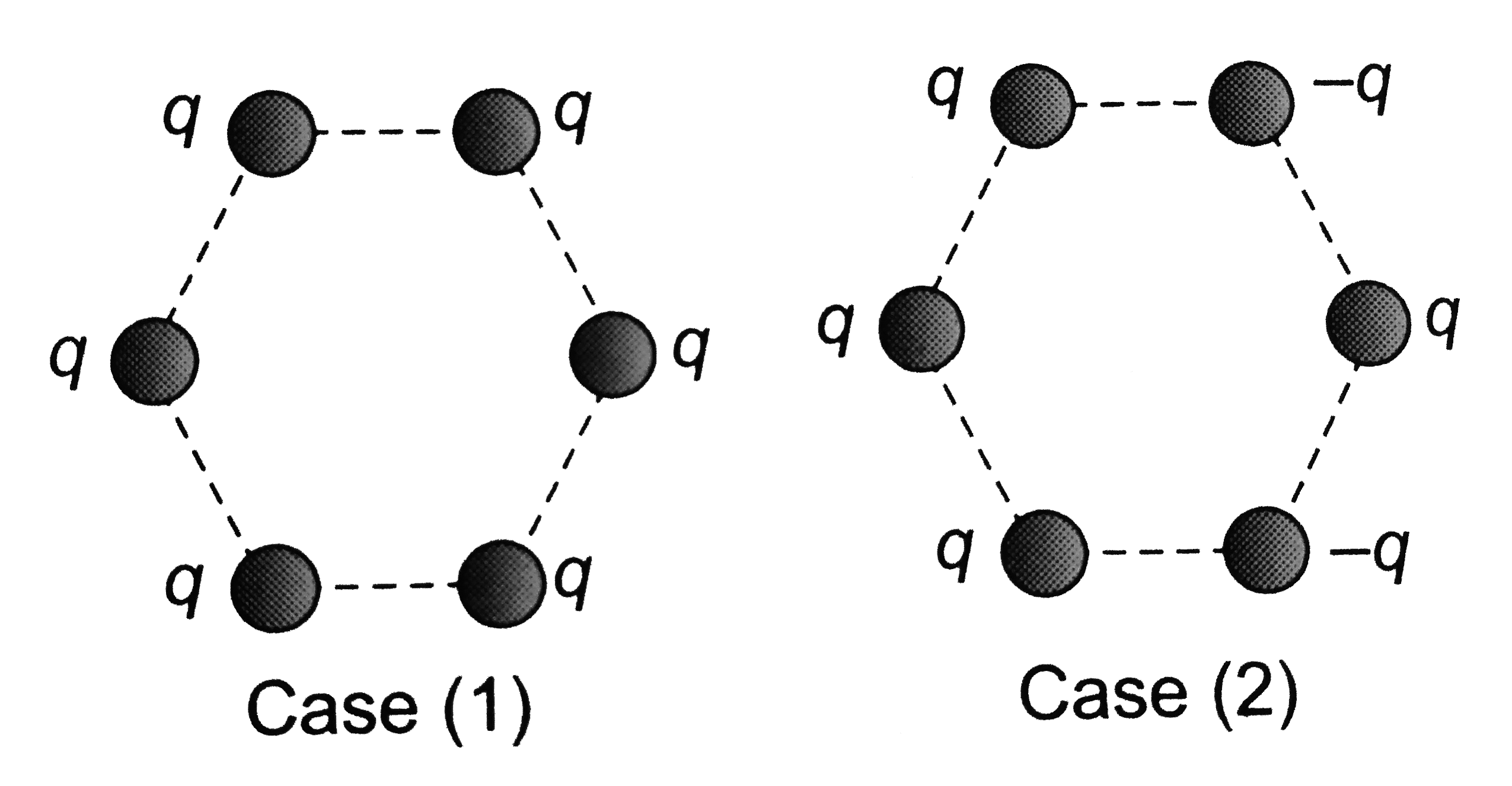
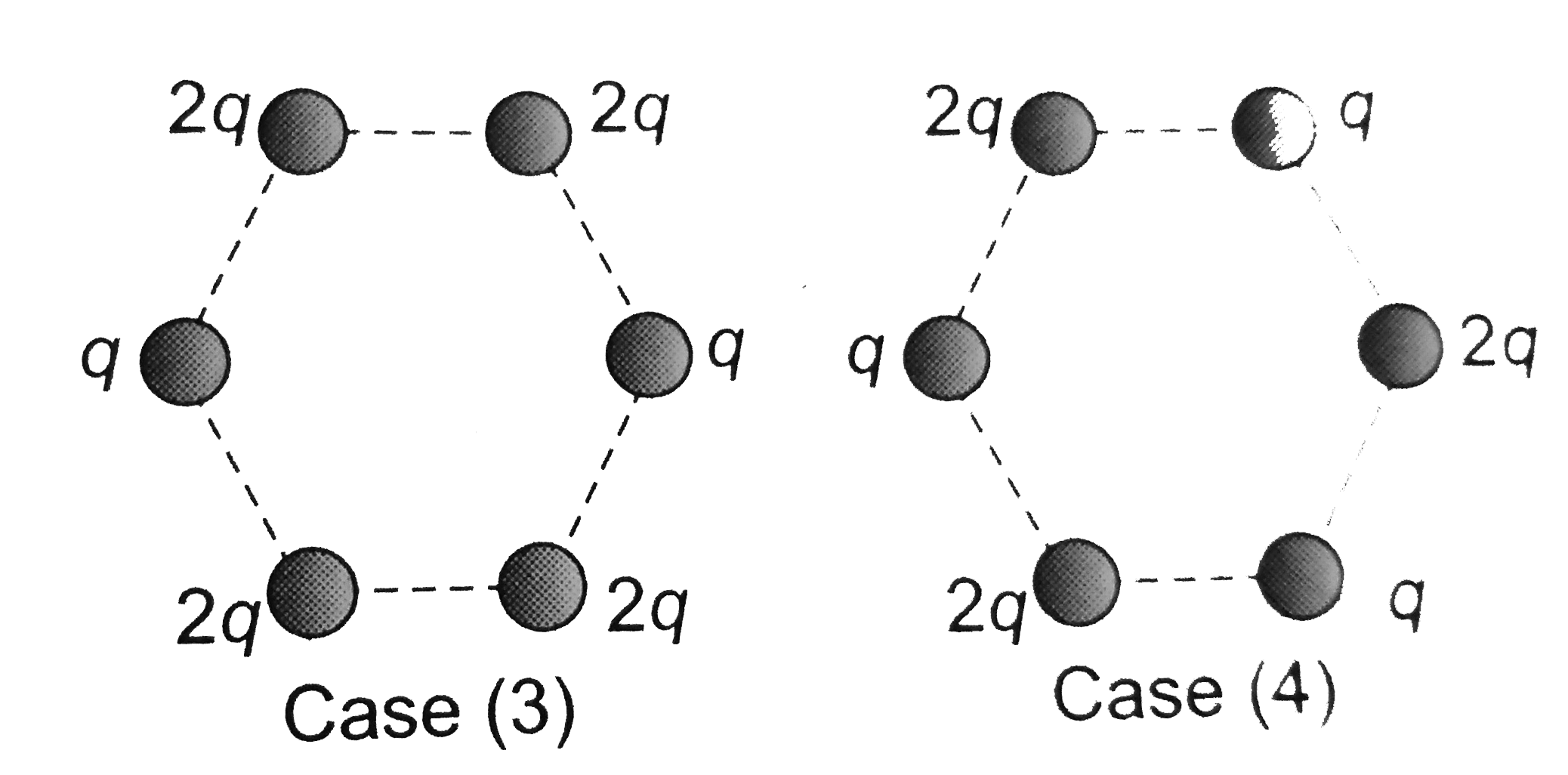
View SolutionFigure below show regular hexagons with charges at the vertices. In which of the following cases the electric field at the centre is not zero
View SolutionA spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it without altering the charge. Will the field inside be changed? What happend if the shell is made of a metal?
View SolutionA spherical conductor of radius 10 cm has a charge of 3.2 x 10^-7 C distributed uniformly. What is magnitude of electric field at point 15 cm from centre of sphere?
View SolutionA cjircular wire-loop of radius a carries a total charge Q distributed uniformly over its length . A small length dL of the wire is cut off. Find the electric field at the centre due to remaining wire.
View Solution
