A wire of linear mass density λ(kg/m) is bent into an arc of a circle of radius R subtending an angle 2θ0 at the centre. Calculate the moment o inertia of this circular arc about an axis passing through its midpoint (M) and perpendicular to its plane. 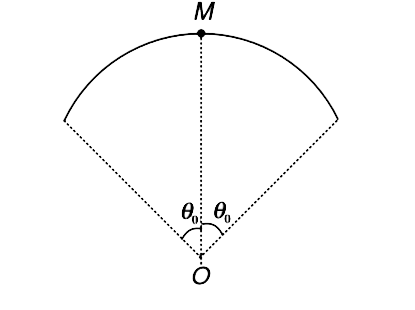
The correct Answer is:I=4λR3(θ0−sinθ0)
Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View Solution
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Calculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View Solution
