An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
Consider an air chamber of volume V with a long nech of uniform area of cross-section A, and a frictioless ball of mass m fitted smoothly in the nech at position , C Fig. the pressure of air below the bal inside the chamber is equal to the atmospheric pressure. Increase the pressure on the ball by a little amount p, so that the ball is depressed to position D, where CD=y
There will be decreases in volume and hence increase in pressure of air inside the chamber . The decrease in volume of the air inside the chamber , ΔV=Ay
Volumetric strain =Charge in volume/original volume
=ΔVV=AyV
∴ Bulk modulus of electricity E, will be
E=stress (or increase in pressure ) /Volumetric strain
=−pAy/V=−pVAy
Here, negative sign shows that the increase in pressure with decrease the volume of air in the chamber.
Now, p=−EAyV
Due to thisi excess pressure, the restoring force acting on the ball is
F=p×A=−EAyV.A=−EA2Vy....(i)
Since F∝y and negative sign show that the force is directed towards equilibrium position. if the applied increased pressure is removed from the ball , the ball will start executing linear SHM in the nech of chamber with C as mean position .
In S.H.M , the restoring force,
F=-ky
comparing (i) and (ii),. we have
spring factor, k=EA2/V
Here, inertia factor =mass of ball =m
period , T=2π√inertia factorspring factor
=2π√mEA2/V=2πA,√mVE
∴ Frequency , v=1T=A2π√EmV
Note: if the ball osillates in the nech of chamber under isothermal conditions , thru, E=P=picture of air inside the chamber , when ball is at equilibrium position . if the ball oscillate in the neck of chamber under adiabatic conditions, then E=gP. where g=CP/Cv
Topper's Solved these Questions
Similar Questions
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time periodof oscillations assuming pressure volume variatinos of air to be isothermal.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
Knowledge Check
An air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. Consider diameter of the ball to be equal to that of the neck of the chamber. The ball is then pressed down a little and released. Let the bulk modulus of air is B. The time period of the oscillation of the ball is:
AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2An air chamber of volume V has a long of cross sectional area A. A ball of mass m is fixed sympthlly in the track The ball modulus of air is B ball is pressed down slightly and released, the time period of the oscillation is
A2π√mV2BA2Bπ√2mVBA2C2π√mVBA2Dπ2√mBA2A solid sphere of density σ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
Ap=σ3Bp=3σC4π3√RgD3π2√Rg
An air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal.
View SolutionAn air chamber of volume V has a neck of crosssectional area "a' into which a light ball of mass "m' just fits and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released. If the bulk modulus of air is B the time period of the oscillation of the ball is 2πmxVyBza9. The value of xyq is
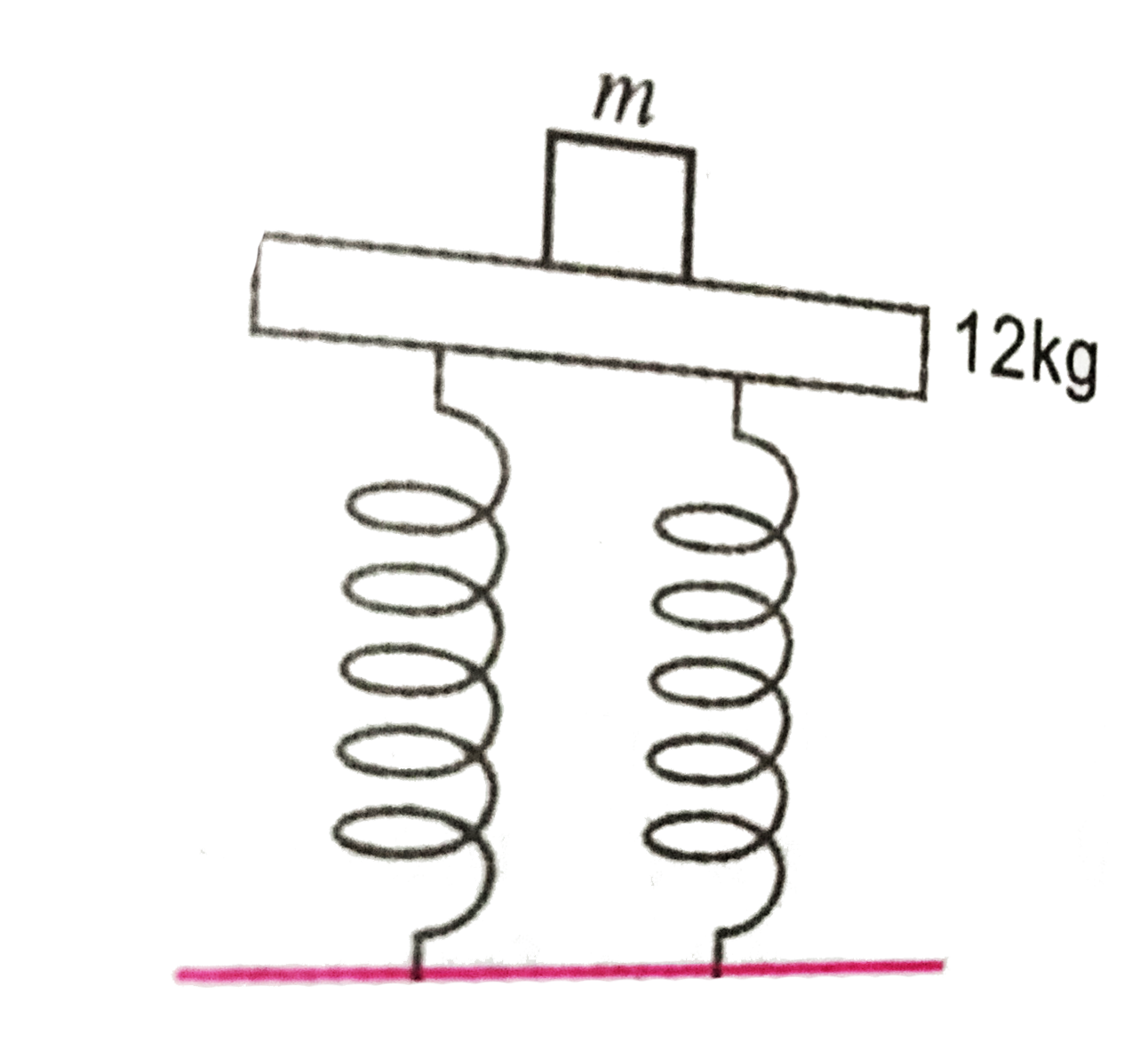
View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
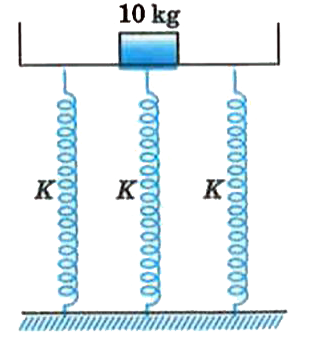
View SolutionAn arrangement of three identical spring and a block of mass 10 kg is shown in the adjoining figure. When the platform on which block is placed is slightly pressed down and released. It performs S.H.M. with a period of 2 s.
(i) Calculate the spring constant of the spring.
(ii) If a block of mass m is further placed on the platform, the new period of S.H.M. becomes 3.5 s. Find the value of m. (Assume platform to be massless)
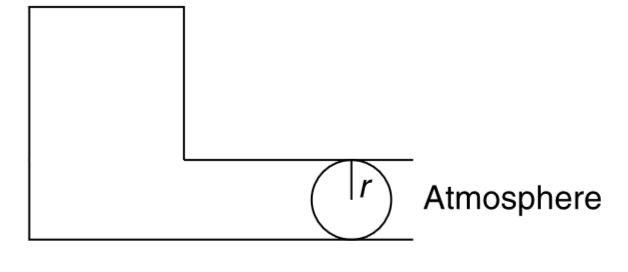
View SolutionA ball of radius r fits tightly inside a tube attached to a container. There is no friction between the tube wall and the ball. Volume of air inside the container is V0 when the ball is in equilibrium. Density of the material of the ball is d and atmospheric pressure is P0. If the ball is displaced a little from its equilibrium position and released, find time period of its oscillation. Assume that temperature in the container remains constant and that air is an ideal gas.
View Solution
