An express train moving at 30 m/s reduces its speed to 10 m/s in a distance of 240 m. If the breaking force is increased by 12.5% in the beginning find the distance that it travels before coming to rest
270 m
240 m
210 m
195 m
The correct Answer is:B
To solve the problem step by step, we will use the equations of motion and the concept of acceleration due to braking force.
Step 1: Identify the given values
- Initial velocity (u) = 30 m/s
- Final velocity (v) = 10 m/s
- Distance traveled (s) = 240 m
Step 2: Use the first equation of motion
We will use the equation:
v2−u2=2as
where a is the acceleration (which will be negative since it is deceleration).
Substituting the known values:
102−302=2a(240)
100−900=480a
−800=480a
a=−800480=−53 m/s2
Step 3: Calculate the new acceleration after increasing the braking force
The braking force is increased by 12.5%. The new acceleration a′ can be calculated as:
a′=1.125×a
Substituting the value of a:
a′=1.125×(−53)
a′=−5×1.1253=−5.6253=−1.875 m/s2
Step 4: Use the second equation of motion to find the distance to come to rest
Now, we need to find the distance s′ that the train travels before coming to rest (final velocity v=0):
Using the equation:
v2−u2=2a′s′
Substituting v=0, u=10 m/s (the speed at which we are starting the new deceleration), and a′=−1.875:
02−102=2(−1.875)s′
−100=−3.75s′
s′=1003.75=26.67 m
Step 5: Calculate the total distance traveled
The total distance traveled before coming to rest is the distance already traveled (240 m) plus the distance traveled during the new deceleration (26.67 m):
Total distance=240+26.67=266.67 m
Final Answer
The total distance that the train travels before coming to rest is approximately 266.67 meters.
---
- Initial velocity (u) = 30 m/s
- Final velocity (v) = 10 m/s
- Distance traveled (s) = 240 m
We will use the equation:
v2−u2=2as
where a is the acceleration (which will be negative since it is deceleration).
102−302=2a(240)
100−900=480a
−800=480a
a=−800480=−53 m/s2
The braking force is increased by 12.5%. The new acceleration a′ can be calculated as:
a′=1.125×a
Substituting the value of a:
a′=1.125×(−53)
a′=−5×1.1253=−5.6253=−1.875 m/s2
Now, we need to find the distance s′ that the train travels before coming to rest (final velocity v=0):
Using the equation:
v2−u2=2a′s′
Substituting v=0, u=10 m/s (the speed at which we are starting the new deceleration), and a′=−1.875:
02−102=2(−1.875)s′
−100=−3.75s′
s′=1003.75=26.67 m
The total distance traveled before coming to rest is the distance already traveled (240 m) plus the distance traveled during the new deceleration (26.67 m):
Total distance=240+26.67=266.67 m
The total distance that the train travels before coming to rest is approximately 266.67 meters.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
The speed of a train is reduced from 60 km/h, to 15 km/h, while it travels a distance of 450 m. If the retardation is uniform, find how much further it will travel before coming to rest ?
View SolutionIf a train travelling at 72 km/h is to be brought to rest in a distance of 200m, then its retardation should be:-
View SolutionA block is projected along a rough horizontal road with a speed of 10 m/s. If the coefficient of kinetic friction is 0.10, how far will it travel before coming to rest?
View SolutionA conveyor belt is moving at a constant speed of 2m/s . A box is gently dropped on it. The coefficient of friction between them is μ=0.5 . The distance that the box will move relative to belt before coming to rest on it taking g=10ms−2 is:
View SolutionInitially a car is moving with speed of 20ms−1 and covers a distance of 100 m before it comes to rest. On making the initial speed of car 40ms−1 keeping the acceleration same, the distance travelled by car before it comes to rest is
View SolutionBlocks A and B each of mass 1kg are moving with 4m/s and 2m/s respectively as shown. The coefficient of friction for all surface is 0.10. Find the distance (in m) by which centre of mass will travell before coming to rest. Assume large distance between the blocks
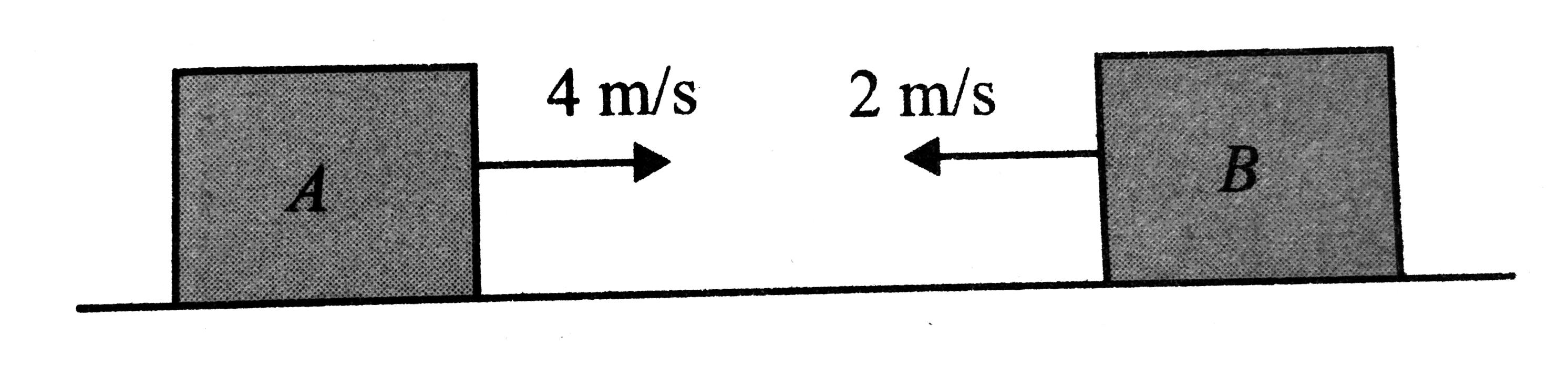
View SolutionA vehicle is moving at a speed of 30 m/s on a circular road of radius 450 m. Its speed is increasing at a rate of 2ms2 . The acceleration of particle at this instant is
View SolutionA train moving with uniform speed covers a distance of 120 m in 2 s. Calculate : (i) the speed of the train, (ii) the time it will take to cover 240 m.
View SolutionA bullet going with speed 350 m/s enters concrete wall and penetrates a distance of 5.0 cm before coming to rest. Find the deceleration.
View SolutionA scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View Solution
