The acceleration of a particle is increasing linerly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
v0t+13bt2
v0t+12bt2
v0t+16bt3
v0t+13bt3
The correct Answer is:C
Step by step video & image solution for The acceleration of a particle is increasing linerly with time t as bt. The particle starts from the origin with an initial velocity v_(0). The distance travelled by the particle in time t will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
The acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
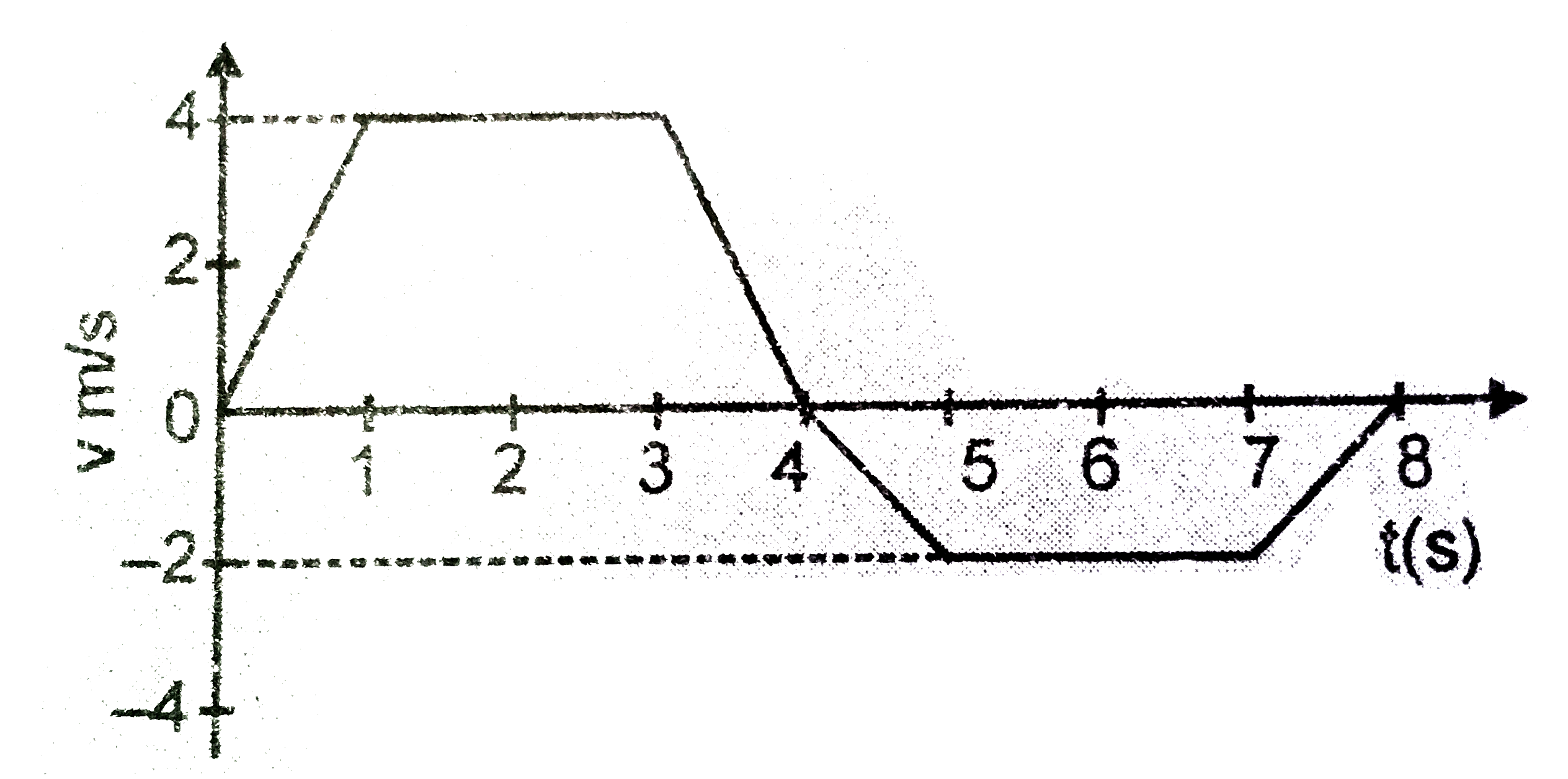
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionThe position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
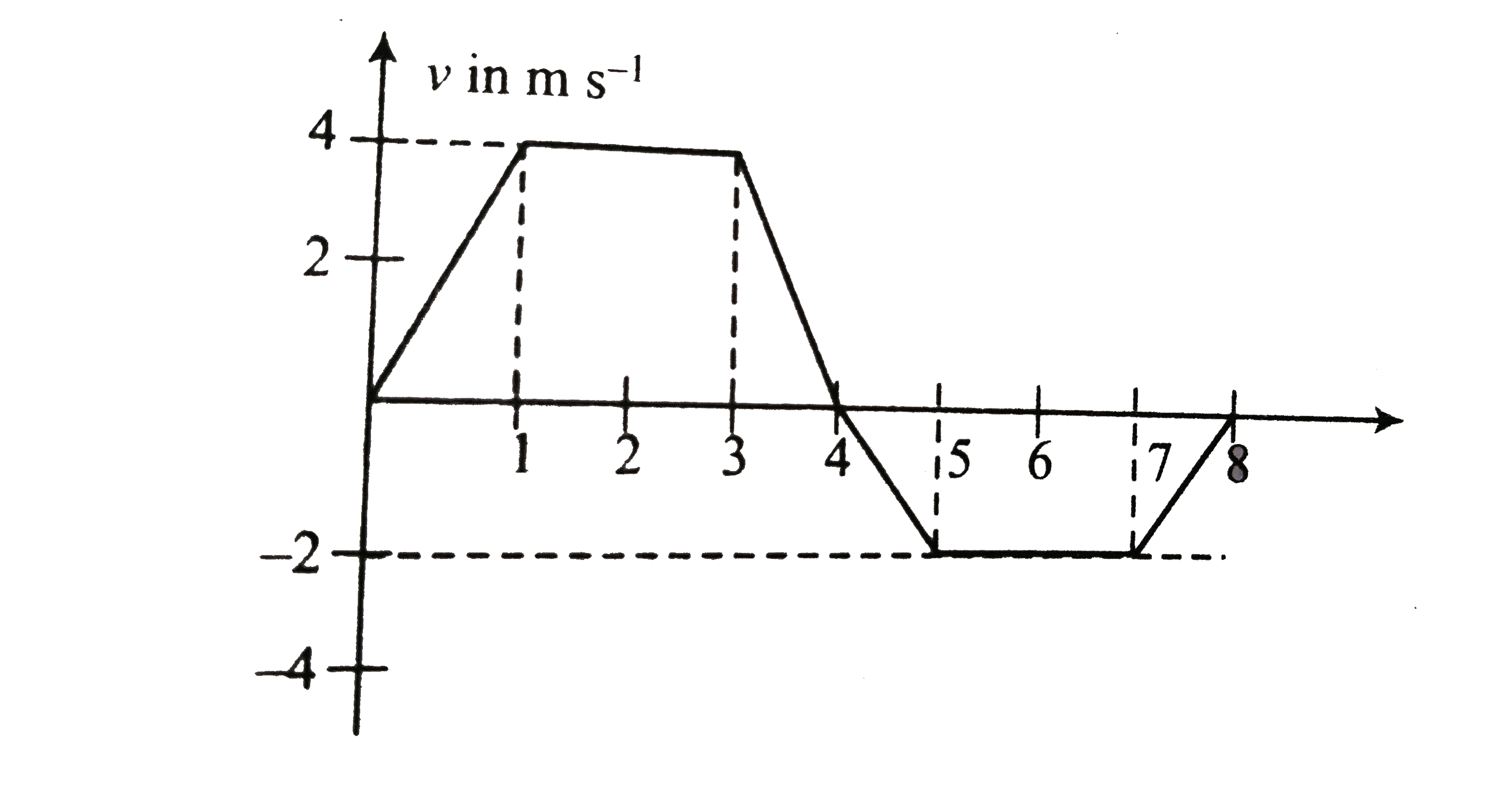 .
.
The distance of the particle from the origin after 8s is .
View SolutionThe velocity time graph of a particle moving along a straight line is shown in the figure. In the time interval from t=0 to t=8 second, answer the following three question.

The distance travelled by the particle is :
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
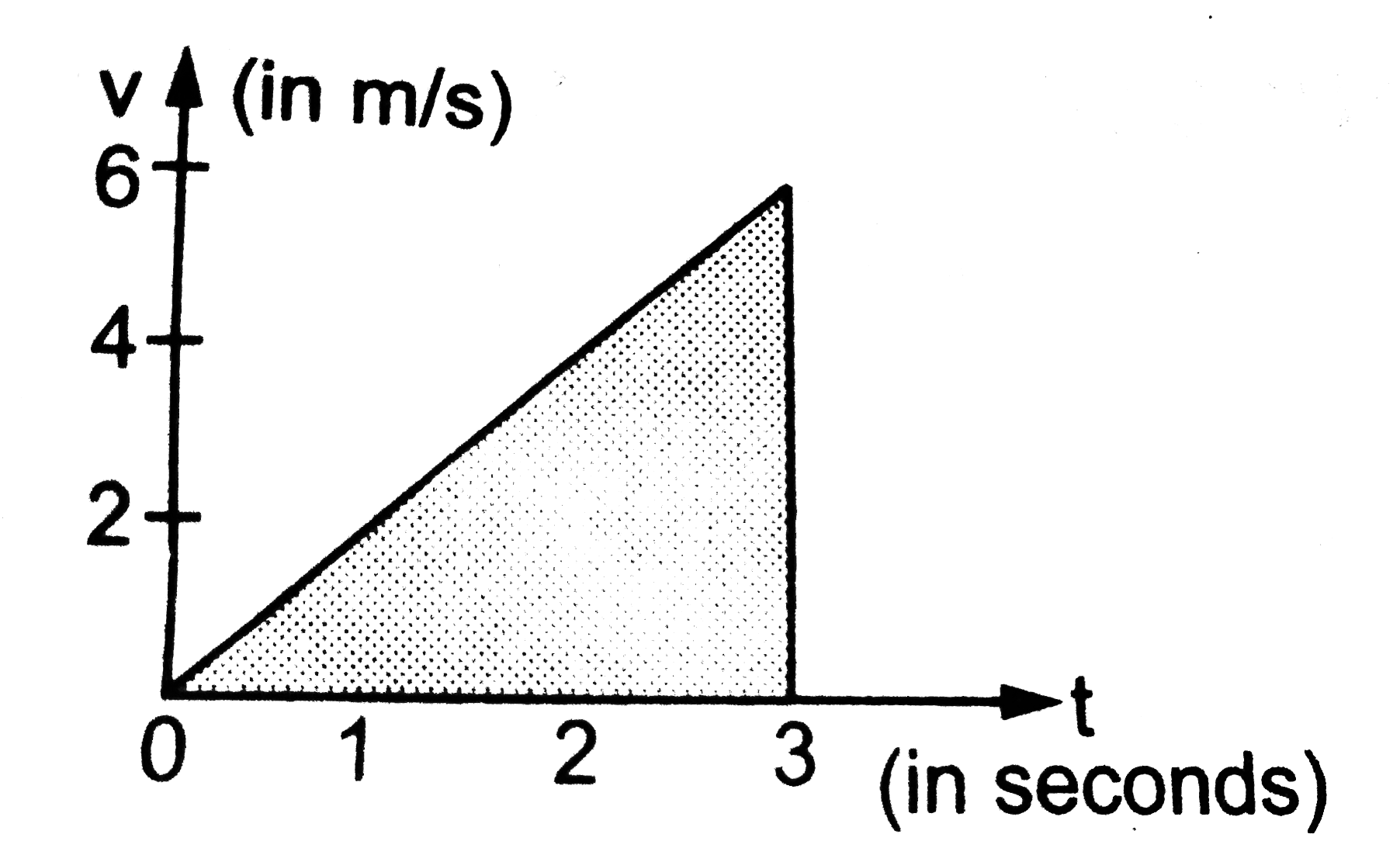
View SolutionA particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View Solution
