An ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.
(a) Here p1=np1,p1V1=p0V0,
np1Vγ1=p0Vγ0
Q'2=RT1nV0V1,Q1=CVT0(n−1)
But nVγ−11=Vγ−10 or,V1=V0n−1γ−1
Q'2=RT01nn1γ−1=RT0γ−11nn
Thus η=1−1nnn−1, on using CV=Rγ−1
(b) Here V2=nV1,p1V1=p1V0
and p1(nV1)γ=p0V0
i.e, nγVγ−11=Vγ−10 or V1=n−γγ−1V0
Also Q1=CpT0(n−1),Q'2=RT01nV0V1
or Q'2=RT01nnγγ−1=Rγγ−1T01nn=CpT01nn
Thus η=1−1nnn−1.
 ,
,
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View SolutionThe condition are the same as in the foregoing problem with the exception that the isothermal process proceeds at the maximum temperature of the whole cycle.
View Solution
Knowledge Check
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnKA cycle is made of three process is iso barie, adiabatic and isothermal. Isothermal process has minimum temperature. Absolute temperature charges by k times withing the cycle. Find out the efficiency.
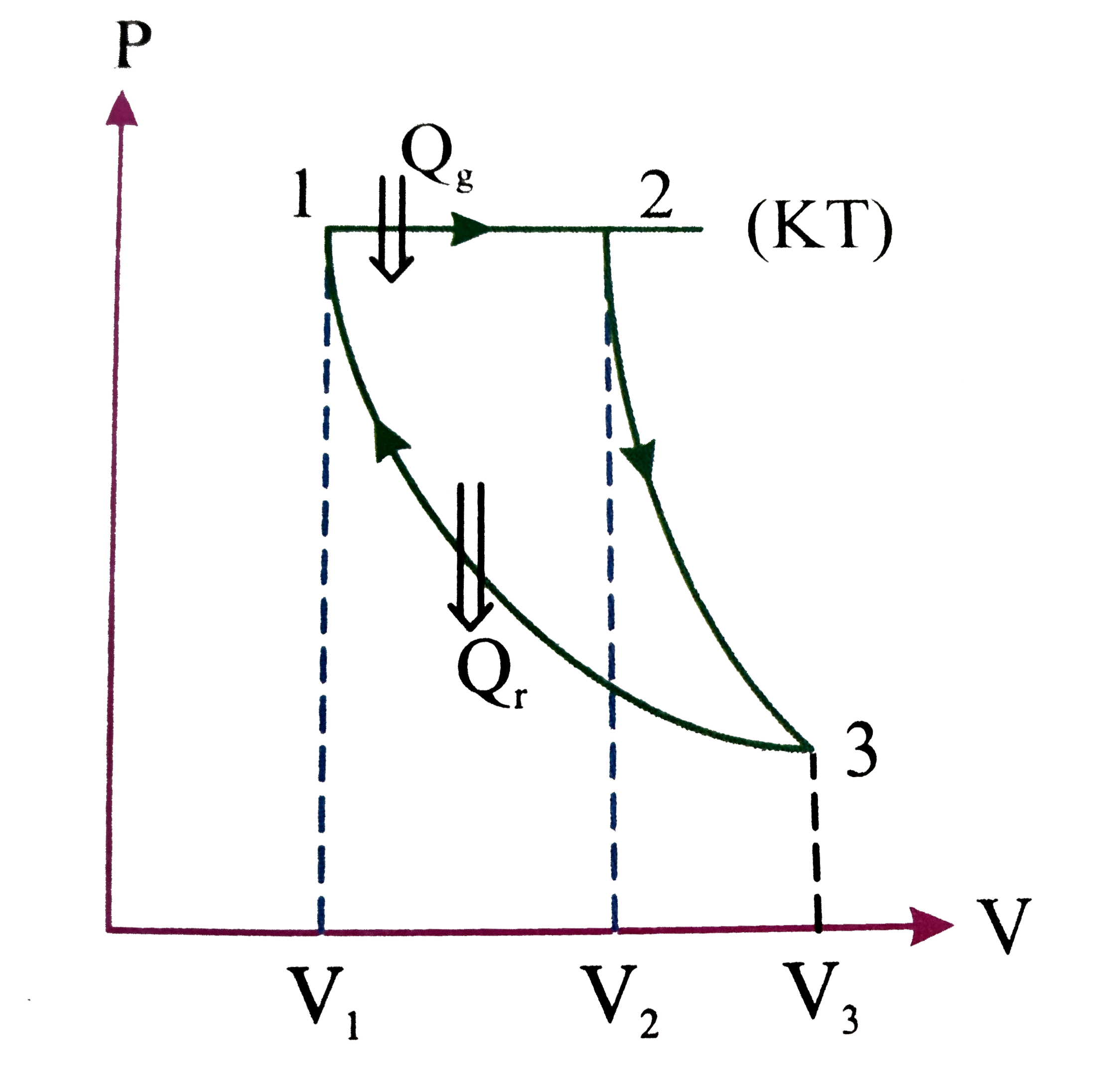 A1−1nK(K−1)B1+1nK(K−1)C1+1nK(K+1)Dnone of these
A1−1nK(K−1)B1+1nK(K−1)C1+1nK(K+1)Dnone of theseAn ideal gas undergoes a process consisting of adiabatic and isothermal process only as shown in the figure. Then :
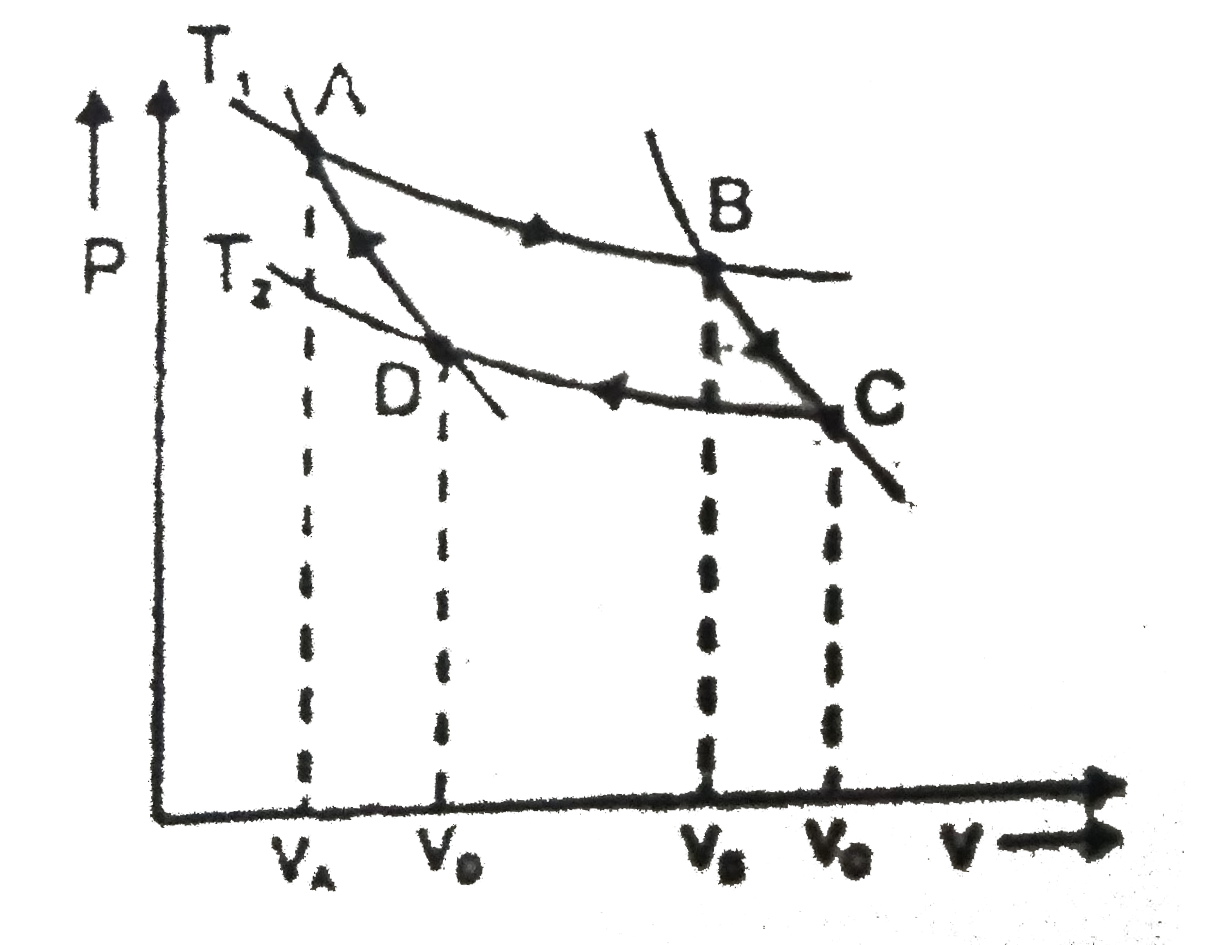 AT1<T2BVAVC=VBVDCwork done by the gas in process will be negativeDefficiency =WAB+WBCQAB
AT1<T2BVAVC=VBVDCwork done by the gas in process will be negativeDefficiency =WAB+WBCQAB
An ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1,T2 and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion.
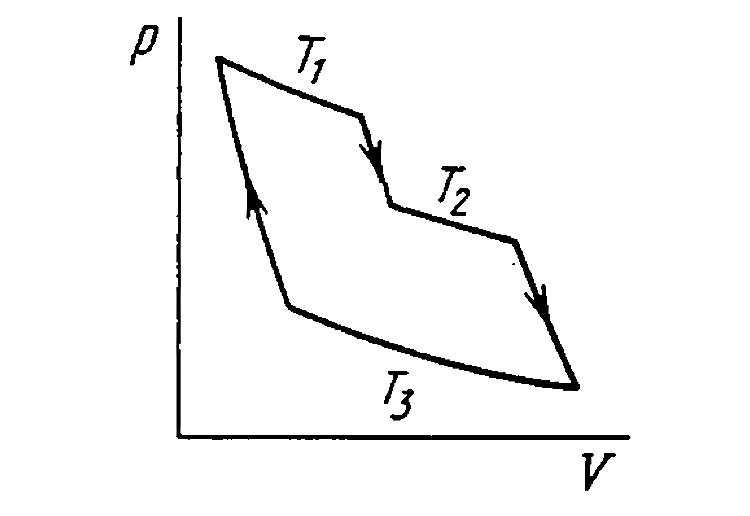 .
.
View SolutionAn ideal gas with the adiabatic exponent γ goes through a cycle (Fig. 2.3) within which the absolute temperature varies τ−fold. Find the efficiency of this cycle.
 .
.
View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)

View SolutionOne mole of an ideal gas is taken through a cyclic process. The minimum temperature during the cycle is 300K. Then, net exchange of heat for complete cycle is
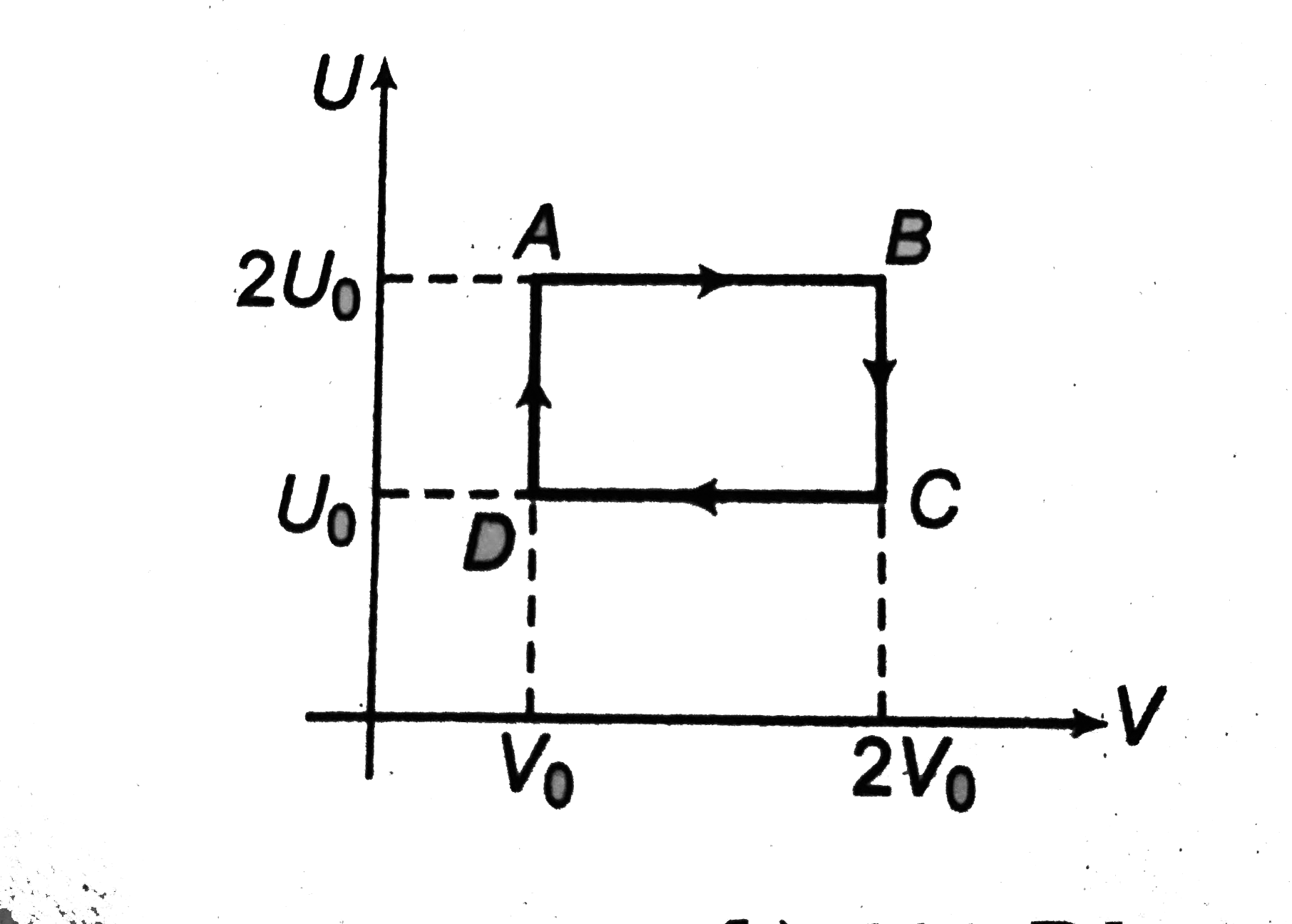
View Solution
