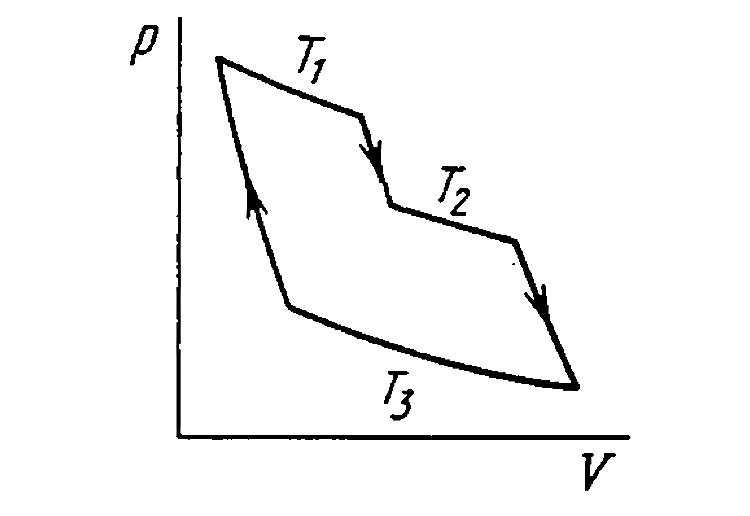
An ideal gas goes through a cycle consisting of alternate isothermal and adiabatic curves (Fig. 2.2). The isothermal processes proceed at the temperatures T1,T2 and T3. Find the efficiency of such a cycle, if in each isothermal expansion the gas volume increases in the same alphaortion.
 .
.
Given V2=nV1,V4=nV3
Q1 = Heat taken at the upper temperature
=RT11nn+RT21nn=R(T1+T2)1nn
Now T1Vγ−12=T2Vγ−13 or V3=(T1T2)1γ−1V2
Similarly V5=(T2T3)1γ−1V4,V6=(T1T3)1γ−1V1
Thus Q2 = heat ejected at the lower temperature =−RT31nV6V5
=−RT31n(T1T2)1γ−1V1V4=−RT31n(T1T2)1γ−1V2n2V3
=−RT31n(T1T2)1γ−11n2(T1T2)−1γ−1=2RT31nn
Thus η=1−2T3T1+T2.
 .
.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects
25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Phase Transformations
35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
An ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies n−fold within the cycle.
View SolutionAn ideal gas goes through a cycle consisting of
(a) isochoric, adiabatic, and isothermal lines ,
(b) isobaric, adiabatic, and isothermal lines,
with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n−fold within the cycle.
View Solution
Knowledge Check
An ideal gas goes through a cycle consisting of ischoric adiabatic and isothermal lines. The isothermal process is perform at minimum temperature. If the absolute temperature varies K times with tn the cycle then find out its effcincy.
 A1−lnKlB1+lnKlClnKlDllnK
A1−lnKlB1+lnKlClnKlDllnKThe isothermal diagram of a gas at three different temperatures T1,T2and_(3), is show in the given figure .Then
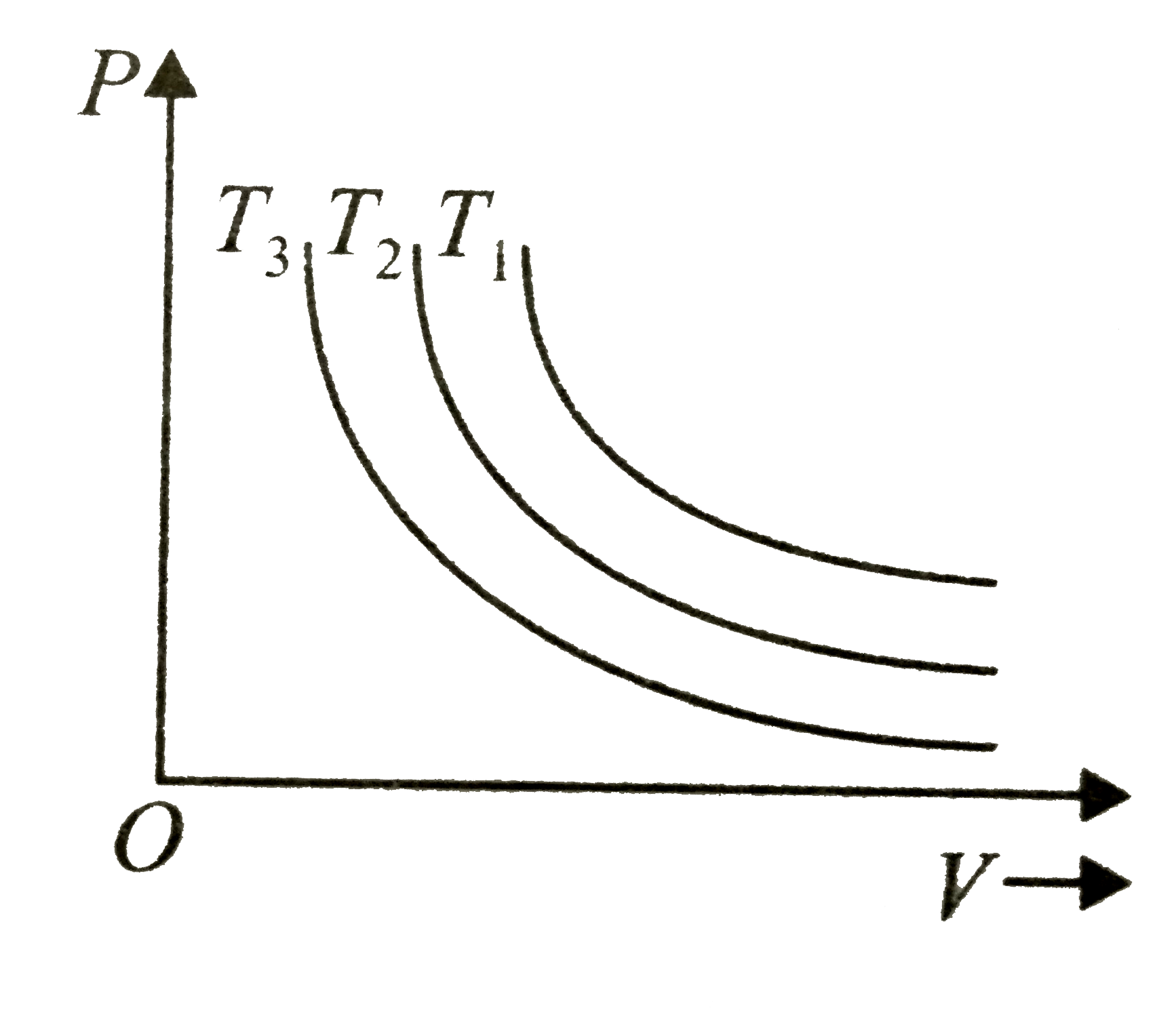 AT1<T2<T3BT1<T2>T3CT1>T2>T3DT1>T2<T3
AT1<T2<T3BT1<T2>T3CT1>T2>T3DT1>T2<T3In following isothermal graphs A, B and C at temperatures T1,T2 and T3, the correct order of temperatures will be :
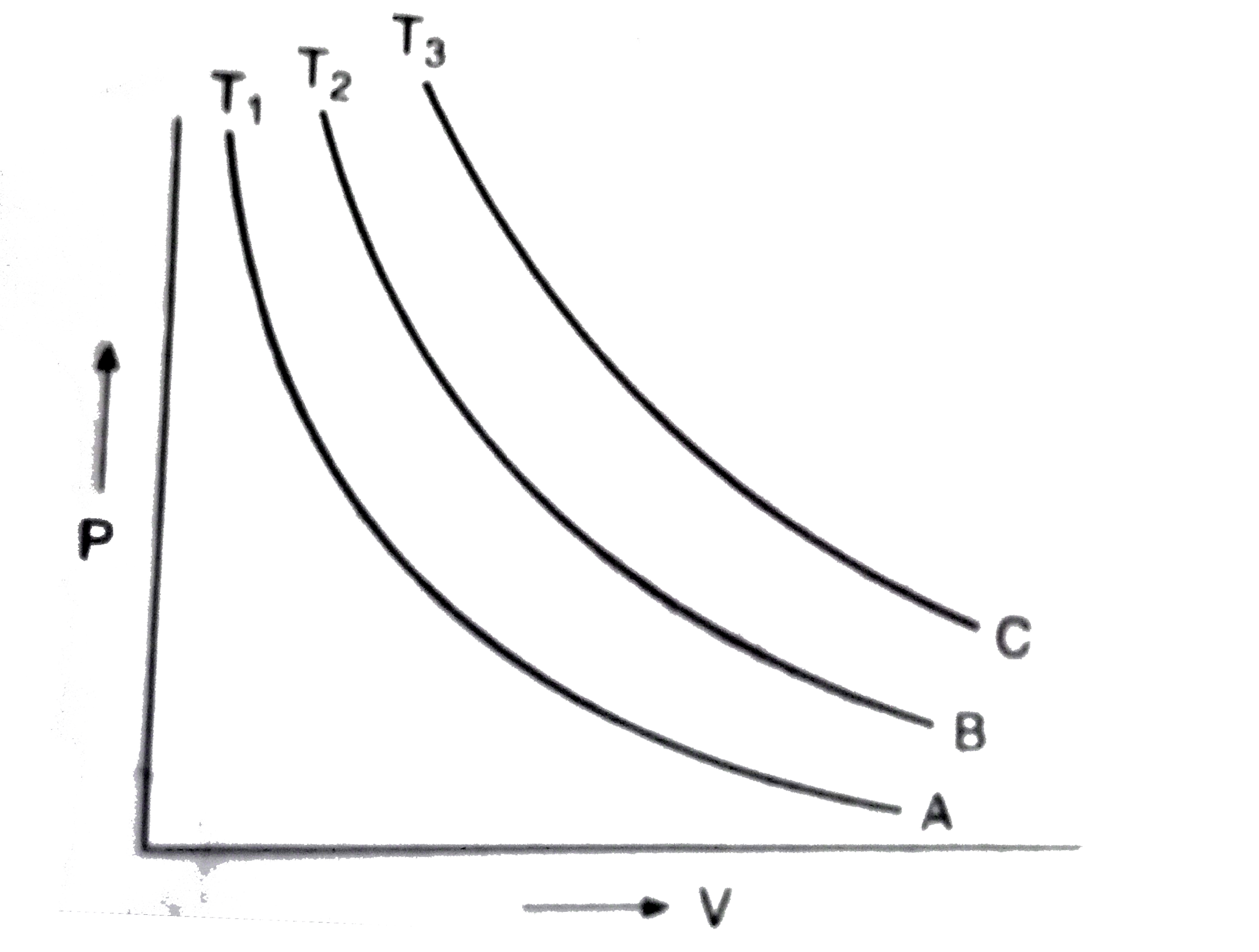 AT1>T2>T3BT1>T3>T2CT3>T2>T1DT3>T2>T2
AT1>T2>T3BT1>T3>T2CT3>T2>T1DT3>T2>T2
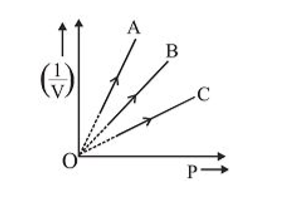
Figure shows the isotherms of a fixed mass of an ideal gas at three temperatures TA,TB and TC , then

View SolutionFigure shows the isotherms of fixed mass of an ideal gas at three temperatures TA.TB and TC then:-
View SolutionState true or false. Wrk done by an ideal gas in aiabatic expansion is less than that in isothermal process (for same temperature range)
View SolutionAn ideal gas with a known γ, completes a cycle consisting of two isotherms and two isobars. The isothermal processes are executed at temperatures T and T'(<T) and isobaric processes are completed at pressures P0 and eP0 [e = base of natural logarithm]. Find the efficiency of the cycle.
View SolutionTwo curves are given at temperatures T1andT2 in an isothermal process, then-
View Solution
