An inductor of inductance 2.0mH s connected across a charged capacitor of capacitance 5.0μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. It is found that the maximum value of charge Q is 200μC.
a. When Q=100μC, what is the value of ∣∣∣dIdt∣∣∣?
b. When Q=200μC, what is the value of I?
c. Find the maximum value of I.
d. When I is equal to one-half its maximum value, what is the value of |Q|?
When Q=100μC, what is the value of \dI/dt\?
When Q=200μC what is the value of I?
Find the maximum value of I.
When I is equal to one-half of its maximum value, what is the value of |Q|?
This is a problem L−C oscillations.
Charge stored in the capacitor oscillates simple harmonically as
Q=Q0sin(ωt±ϕ)
Here Q0=maximum value of Q=200μC=2×10−4C
ω=1√LC=1√(2×10−3)(5.0×10−6)=104s−1
Let at t=0,Q=Q0 then
Q(t)=Q0cosωt ........i
I(t)=dQdt=−Q0ωsinωt and ........ii
dI(t)dt=−Q0ω2cosωt ............iii
a. Q=100μC
or Q02 at cosωt=12
or ωt=π3
At cosωt=12, from eqn iii:
∣∣∣dIdt∣∣∣=(2.0×10−4C)(104s−1)2(12)
∣∣∣dIdt∣∣∣=104A/s
b. Q=200μC or Q0 when cosωt=1, i.e. cosωt=0,2π........
At the time I(t)=−Q0ωsinωt
or I(t)=0(sin02=sin2π=0)
c. I(t)=−Q0ωsinωt
∴ Maximum value of I is Q0ω
Imax=Q0ω=(2.0×10−4)(104)
Imax=2.0A
d. From energy conservation
12LI2max=12LI2+12Q2C
or Q=√LC(I2max−I2)
I=Imax2=1.0A
∴Q=√(2.0×10−3)(5.0×10−−6)(22−12)
Q=√3×10−4C
or Q=1.732×10−4C
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 5
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 6
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 3
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
An inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View SolutionAn inductor of inductance 2 mH is connected across a charged capacitor of 5 μ F . Let q denote the instaneous charge on the capacitor and i the current in the circuit . Maximum value of charge is Q = 200 μ C.
(a) When Q = 100 μ C what is the value of /di/dt / ?
(b) When Q = 200 μ C what is the value of i ?
View SolutionThe charge on the condenser of capacitance 2μF in the following circuit will be -
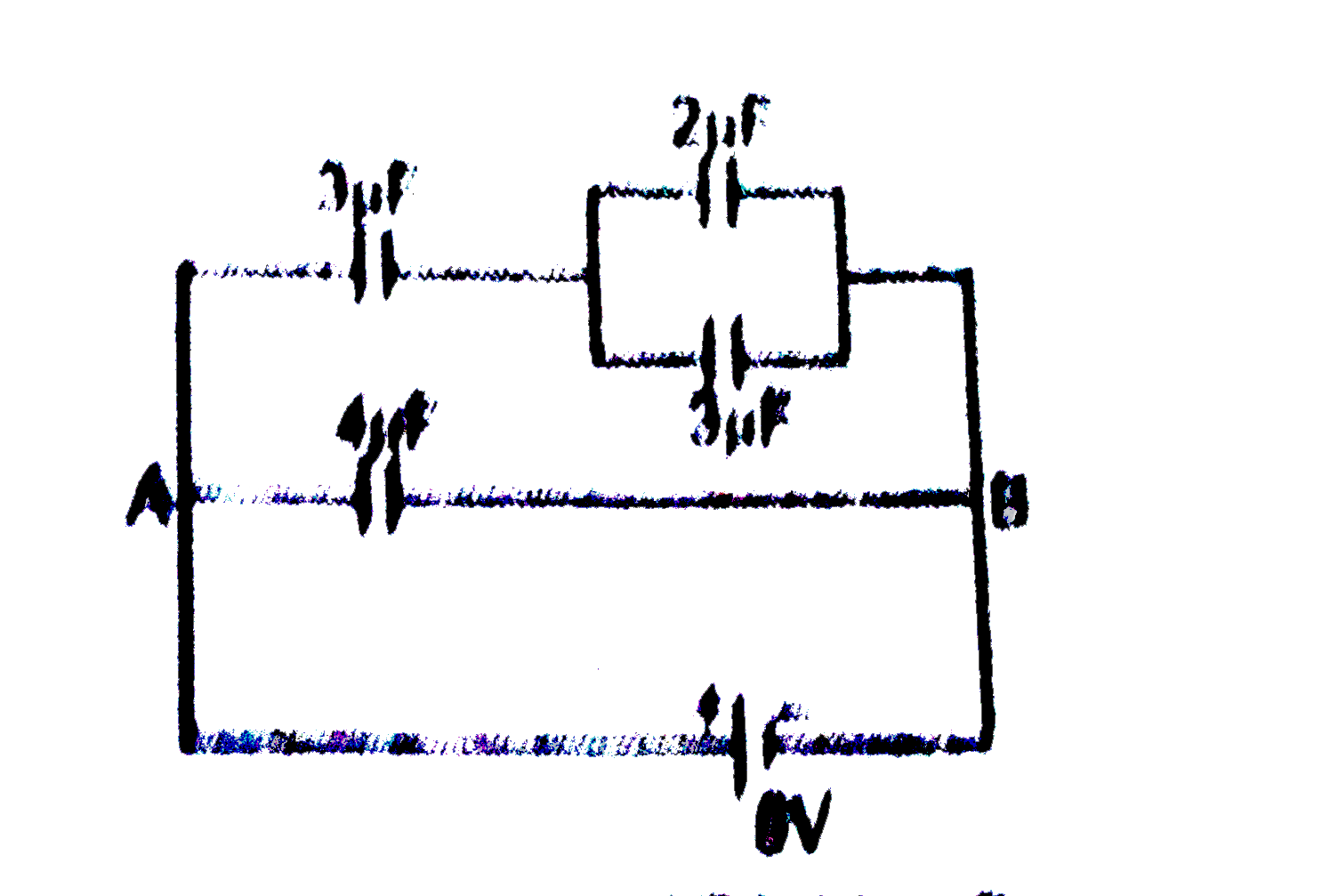
View SolutionThe charge on 4μFcapacitor in the given circuit is (inμC)

View SolutionThe charge in the 2μF capacitor at steady state is
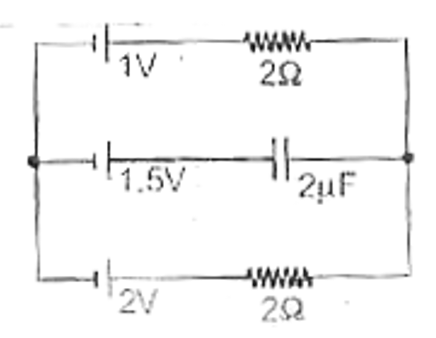
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
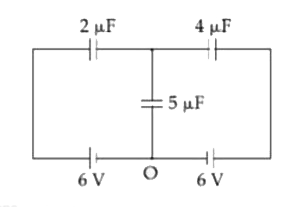
View SolutionIn the given circuit, the charge on 4μF capacitor will be :

View SolutionA capacitor of capacitance 2μF is connected in the tank circuit of an oscillator oscillating with a frequency of 1 kHz. If the current flowing in the circuit is 2mA, the voltage across the capacitor will be
View SolutionIn the given circuit, the charge on 4μF capacitor will be :
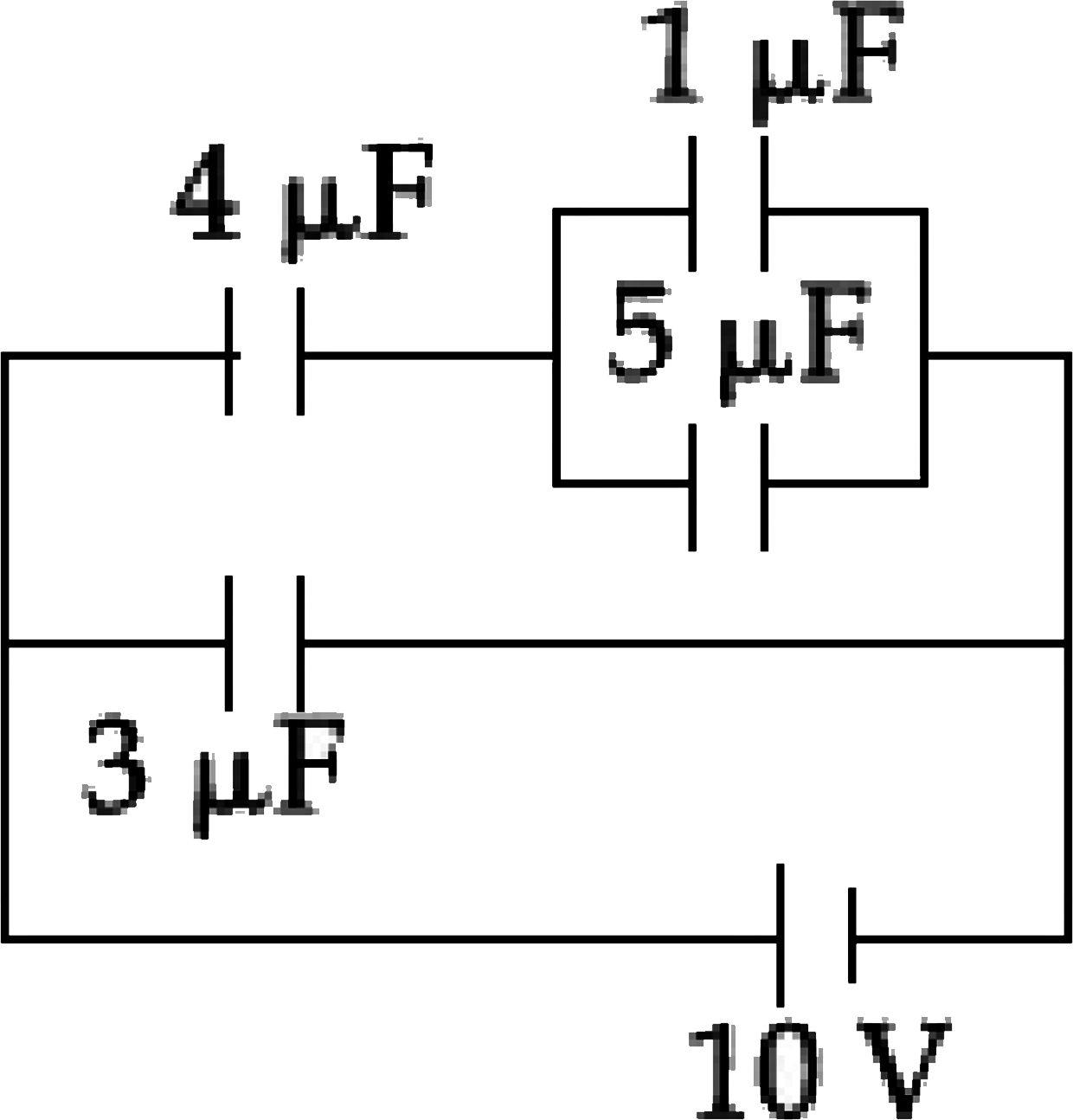 .
.
View SolutionA capacitor of capacitance 1μF is charged to potential 2 V and is connected to an inductor of 1 mH. At an instant when potential difference across. The capacitor is 1 V, the current in the circuit is 10−2√10x3 ampere. Find out the value of x.
View Solution
