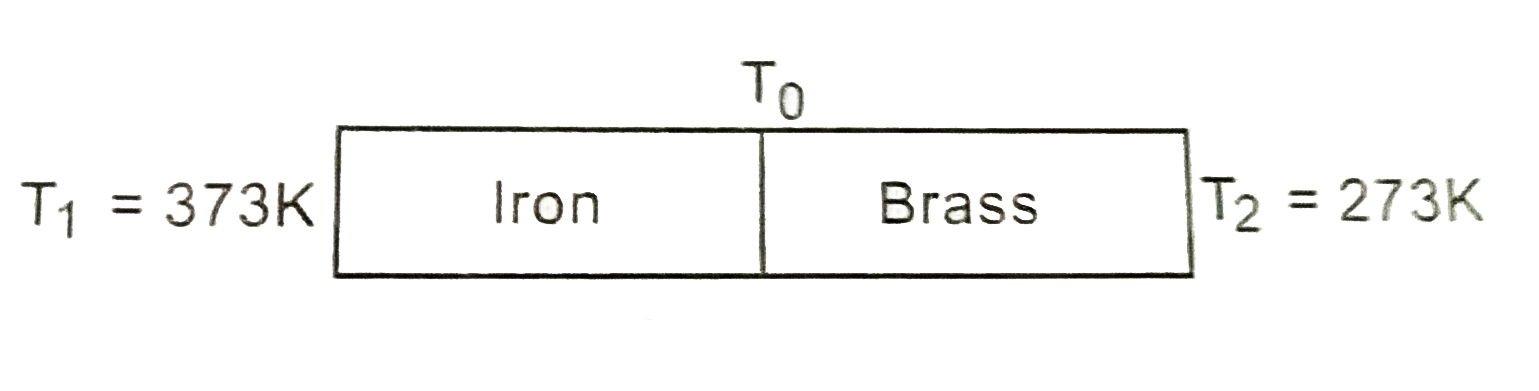
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
Given, Length L1=L2=L=0.1m
Area, A1=A2=A=0.02m2
Thermal conductivity, K1= 79 Wm−1K−1,K2=109Wm−1K−1
Temperature , T1=373 K and T2=273K
At steady state, heat transferred from any section of thermal conductor is same i.e. H1=H2=H
⇒(K1A1(T1−T0)L1=(K2A2(T0−T2)L2).......(ii)<br>ForA_(1)=A_(2)=AandL_(1) = L_(2) = L,Eq.(i)becomesK_(1)(T_(1)-T_(0)) = K_(2)(T_(0)-T_(2)) rArrT_(0)=(K_(1)T_(1)+K_(2)T_(2))/(K_(1)+K_(2))<br>Therefore,heatcurrentthroughother¯¯¯¯¯¯<br>H= (K_(1)A(T_(1)-T_(0)))/L=(K_(2)A(T_(0)-T_(2)))/L = A(T_(1)-T_(2))/(L(1/K_(1)+1/K_(2)))<br>Now,heatcurrentthroughcomposite¯of≤n>hL_(1)+L_(2) = 2Land≡a≤ntthermalconductivityK^('),canbegivenby<br>H^(') = (K^(')A(T_(1)-T_(2)))/(2L) = H rArrK=(2K_(1)K_(2))/(K_(1)+K_(2))<br>(i)So,thetemperatureofthejunctionoftwo¯sis<br>T0=K1T1+K2K2K1+K2
=79Wm−1×373K+109Wm−1K−1×273K79Wm−1K−1+109Wm−1K−1
91.6Wm−1K−1
iii) Heat current through the composite bar
H′=H=(K′AT1−T22L
(91.6 Wm^(-1)K^(-1) xx 0.002m^(3) xx (373 -273)K)/(2 xx 0.1)m
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.1
10 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
The ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
An iron plate 10−5m2 area, 4×10−3 m thick has its opposite faces maintained at 373 K and 223 K respectively. How much heat flows through the plate per second ? Thermal conductivity of iron =80Wm−1K−1.
View SolutionA copper rod of length 75 cm and an iron rod of length 125cm are joined together end to end . Both are of circular cross section with diameter 2 cm . The free ends of the copper and iron are maintained at 100∘C and0∘C respectively . The surface of the bars are insulated thermally . The temperature of the copper -iron junction is [Thermal conductivity of the copper is 386.4W/m−K and that of iron is 48.46W/m−K].
View SolutionA uniform copper rod 50 cm long is insulated on the sides, and has its ends exposedto ice and steam,respectively. If there is a layer of water 1 mm thick at each end, calculate the temperature gradient in the bar. The thermal conductivity of copper is 436Wm−1K−1 and that of water is 0.436Wm−1K−1.
View SolutionA brass boiler has a base area of 0.15m2 and thickness is 1.0cm. It boils water at the rate of 6.0kg/min. When placed on a gas stove. Estimate the temperature of the part of the flame in contact. With the boiler. Thermal conductivity of brass =109Wm−1K−1
View SolutionTwo identical metal rods A and B are joined end to end. The free end of A is kept at 27°C and the free end of B at 37°C. Calculate the temperature of the interface. Thermal conductivity of A=385Wm−1K−1, that of B 110Wm−1K−1.
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K

View SolutionCalculate q,w, and ΔU for the isothermal reversible expansion of one mole of an ideal gas from an initial pressure of 2.0 bar to a final pressure of 0.2 bar at a constant temperature of 273K.
View Solution
