An L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure
a. Find the value of θ0 at equilibrium
b. If it is slightly displacement from its equilibrium position, find the frequency of oscillation.

Taking B as the origin, the coordinate of its c and m are
xC=M2−L2M2+M2=L4
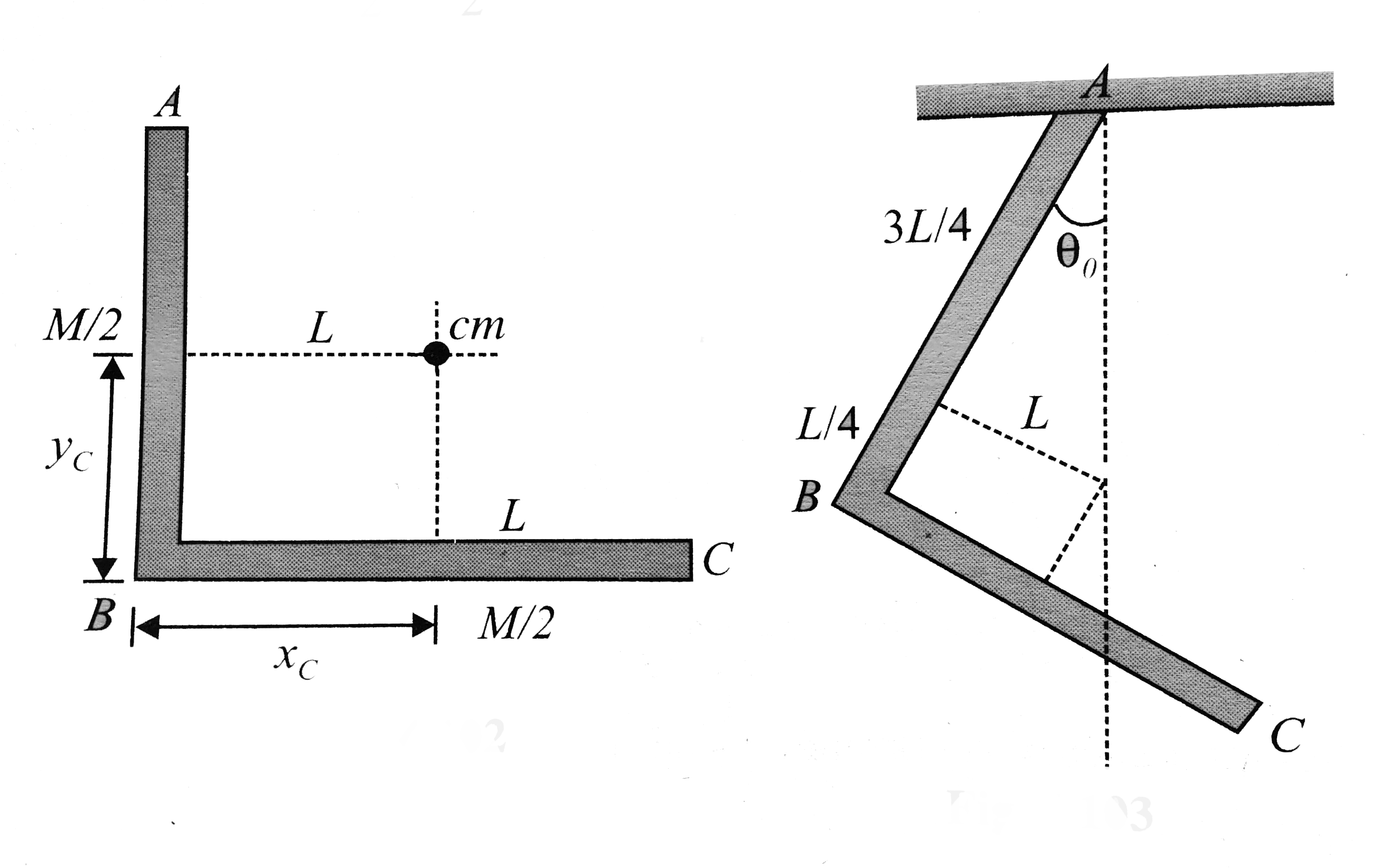

xC=M2−L2M=L4 ⇒tanθ0=L/43L/4=13
θ0=tan1(13)
b. The prequency of oscillation for a compound pendulum is
f=12π√mgtl
where d= distance of the cm from the point of suspension. l= moment of inertia aboutthe point of suspension.
d=√(3L4)2+(L4)2=L4√10
l=(M2)L23+(M2)(L12)+(M2)[L2+(L2)2]=ML23
f=12π
⎷Mg(L)4√10ML23orf=12π√(2.37)gL
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
An L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure
a. Find the value of θ0 at equilibrium
b. If it is slightly displacement from its equilibrium position, find the frequency of oscillation.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
A L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane as shwon. If it is slightly displaced from its equilibrium position then the frequency of oscillation is…….
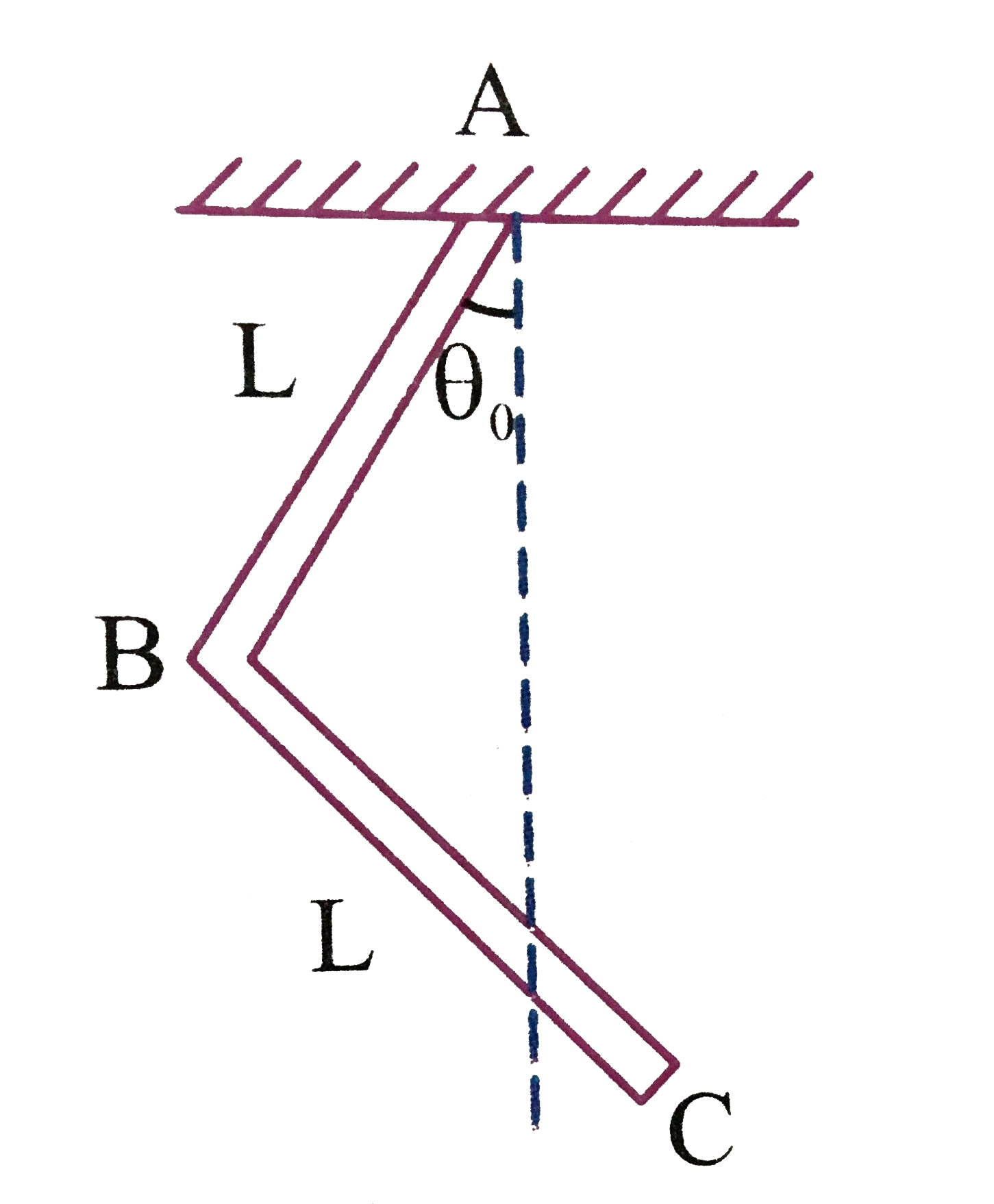 A12π ⎷(gL(3√104)B12π ⎷gL(√104)C12π√gL(√2)D12π√g2L
A12π ⎷(gL(3√104)B12π ⎷gL(√104)C12π√gL(√2)D12π√g2LFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
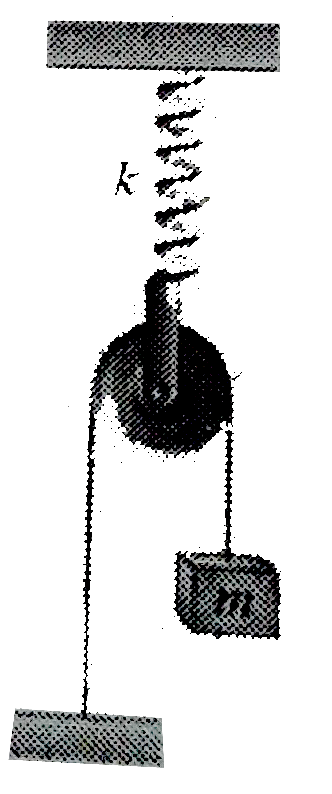 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
A rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
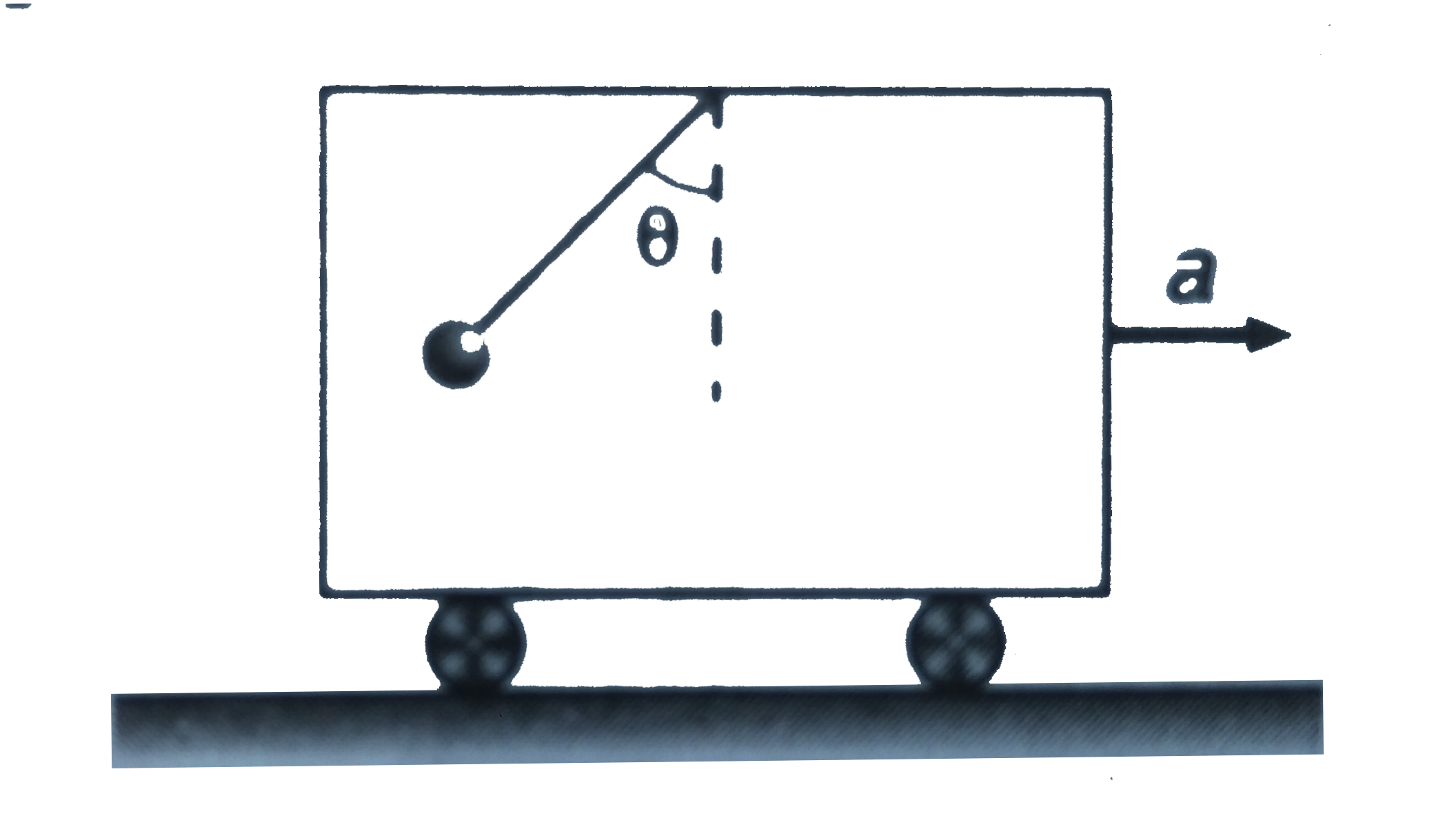
View SolutionA uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
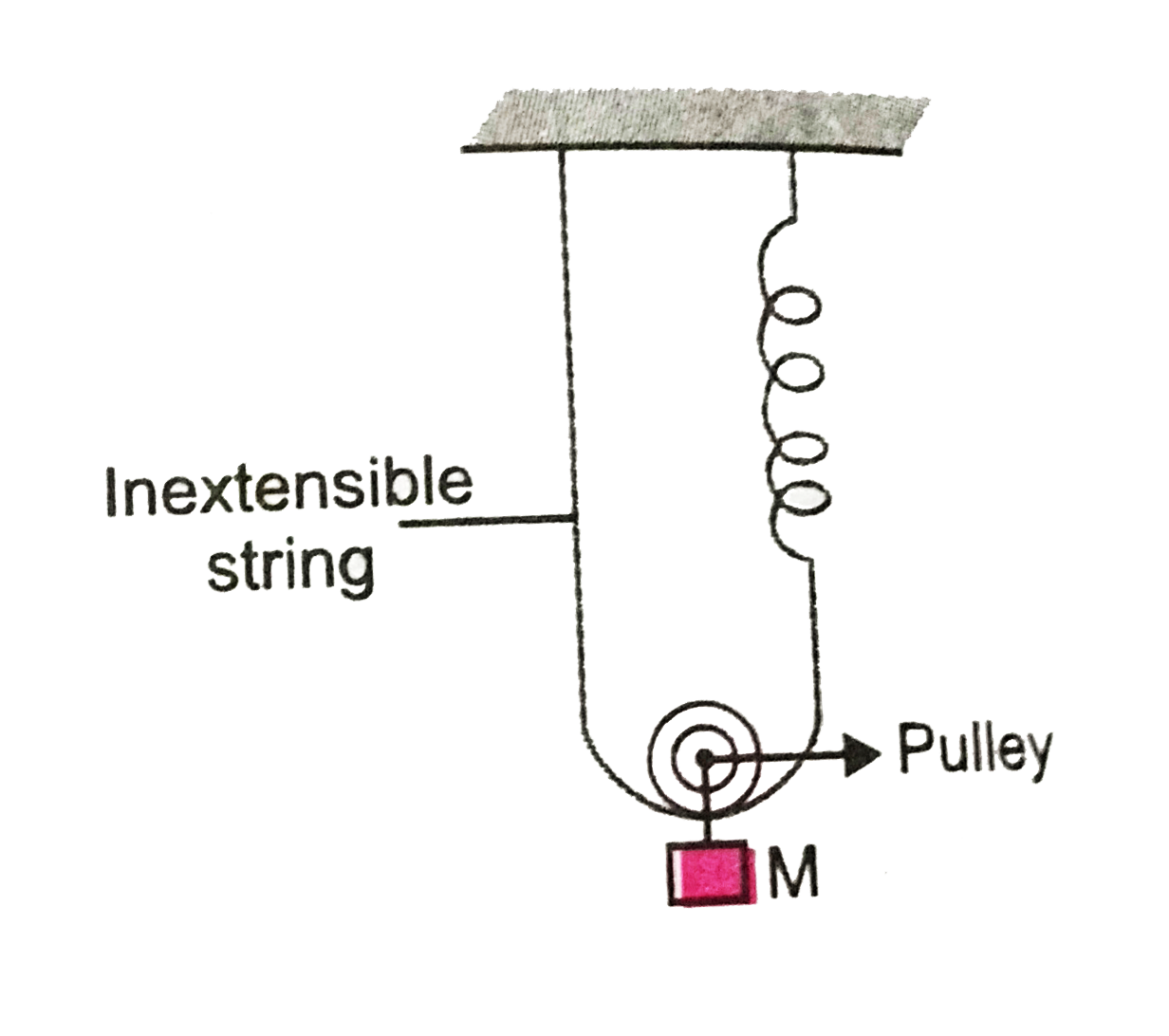
View SolutionConsider the system shown below. If the charge is slightly displaced perpendicular to the wire from its equilibrium position then find out the time period of SHM.
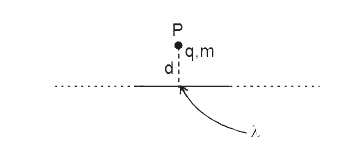
View Solution
