Angle batween velocity and acceleration vectors in the following case
List-IList-II(A)Vertically projected body(e)90∘(b)For freely falling body(f)Changes from point to point(C)For projectile(g)Zero(d)In uniform circular motion(h)180∘
a-h, b-g, c-f, d-e
a-f, b-g, c-h, d-e
a-e, b-f, c-h, d-g
a-g, b-h, c-e, d-f
The correct Answer is:A
To solve the problem of determining the angle between velocity and acceleration vectors for various motion scenarios, we will analyze each case step by step.
1. Vertically Projected Body (A):
- When a body is projected vertically upwards, its velocity vector is directed upwards.
- The acceleration due to gravity acts downwards.
- Therefore, the angle between the velocity vector (upwards) and the acceleration vector (downwards) is 180 degrees.
- Match: A → H (180°)
2. Freely Falling Body (B):
- For a freely falling body, both the velocity and acceleration vectors are directed downwards.
- Since both vectors are in the same direction, the angle between them is 0 degrees.
- Match: B → G (0°)
3. Projectile Motion (C):
- In projectile motion, the velocity vector changes in direction as the projectile moves along its path (it has both horizontal and vertical components).
- However, the acceleration due to gravity always acts downwards.
- As the projectile moves, the angle between the velocity vector and the acceleration vector changes from point to point.
- Match: C → F (changes from point to point)
4. Uniform Circular Motion (D):
- In uniform circular motion, the velocity vector is always tangent to the circular path, while the acceleration vector (centripetal acceleration) points towards the center of the circle.
- The angle between the tangent (velocity) and the radius (acceleration) is 90 degrees.
- Match: D → E (90°)
Final Matches:
- A → H (180°)
- B → G (0°)
- C → F (changes from point to point)
- D → E (90°)
Conclusion:
The correct matches are:
- A with H
- B with G
- C with F
- D with E
- When a body is projected vertically upwards, its velocity vector is directed upwards.
- The acceleration due to gravity acts downwards.
- Therefore, the angle between the velocity vector (upwards) and the acceleration vector (downwards) is 180 degrees.
- Match: A → H (180°)
- For a freely falling body, both the velocity and acceleration vectors are directed downwards.
- Since both vectors are in the same direction, the angle between them is 0 degrees.
- Match: B → G (0°)
- In projectile motion, the velocity vector changes in direction as the projectile moves along its path (it has both horizontal and vertical components).
- However, the acceleration due to gravity always acts downwards.
- As the projectile moves, the angle between the velocity vector and the acceleration vector changes from point to point.
- Match: C → F (changes from point to point)
- In uniform circular motion, the velocity vector is always tangent to the circular path, while the acceleration vector (centripetal acceleration) points towards the center of the circle.
- The angle between the tangent (velocity) and the radius (acceleration) is 90 degrees.
- Match: D → E (90°)
- A → H (180°)
- B → G (0°)
- C → F (changes from point to point)
- D → E (90°)
The correct matches are:
- A with H
- B with G
- C with F
- D with E
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Vectors and Scalars)
5 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-IB (Addition and subtraction of vectors)
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Ascending & descending Order)
2 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
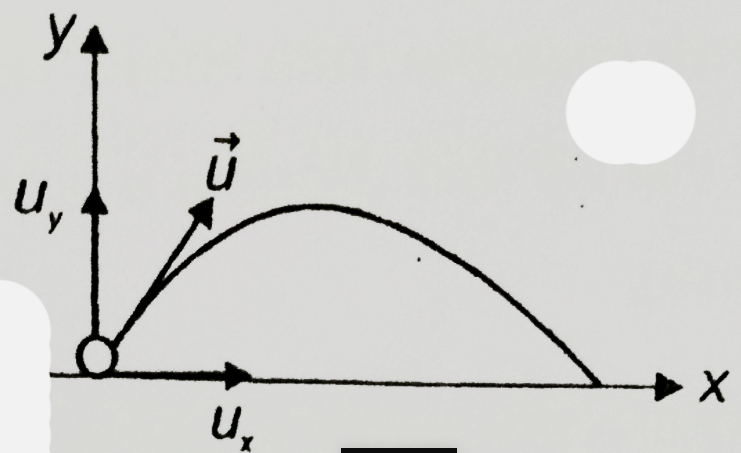
A particle is projected from level ground near the surface of earth with intitial velocity →u=uxˆi+uyˆj ,as shown in the figure. If a(x)anday are the components of acceleration in horizontal and vertically downward directions then
Match the following columns.
(Column I,Column II), ( (A) Projectile motion,(p) Uniform motion)((B) A block sent sliding on a smooth horizontal surface,(q) Unifromly accelerated motion),((C) Unifrom circular motion , (r) motion with non- uniform acceleration),( (D) Swing of pendulum ,(s) Non-uniform motion):}
View SolutionMatch the following :
List - 1List - 2(a)second(e)carbon −12(b)mole(f)Platinum iridium (c)Metre(g)Cs−133(d) Kilogram(h)Kr−86
View Solution
Knowledge Check
Match List I with List II and select the correct answer
List IList II(System)(Expression for moment of inertia)A. A ring about its axis(1)MR2/2B. A uniform circular disc about its axis(2)2/5MR2C. A solid sphere about any diameter(3)7/5MR2D. A solid sphere about any tangent(4)MR2
Selec the answer from the codes given belowAABCD2134BABCD4321CABCD1432DABCD4123
List-IList - 2(a)m−1(e)Surface tension(b)Pa(f)Thermal capacity(c)Jk−1(g)Rydberg constant(d)Jm−2(h)Energy density
View SolutionSome physical constants are given in List-1 and their dimensional formulae are given in List-2. Match the correct pairs in the lists
List-IList-2(a)Planck's constant (e)ML−1T−2(b)Gravitational constant (f)ML−1T−1(c)Bulk modulus(g)ML−2T−1(d)Coefficient of viscosity (h)M−1L3T−2
View SolutionList-IList-2(a)Electron volt(e)746W(b)kWH(f)10−15m(c)Horse power(g)36×105J(d)Fermi(h)1.6×10−19J
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
View SolutionMatch list I with list II for a projectile.
List-IList-II(A)For two angles θand(90−θ)with same magnitude of velocity of projection(e)PˆiPˆig(b)Equation of parabola of projectiley=Px−Qx2(f)Maximum height=25%P2Q(C)Radius of curvature of path of projectile projected with a velocity(Pˆi+Qˆj)ms−1at highest point(g)Range = Maximum height(d)Angles of projectionθ=Tan−1(4)(h)Range is same
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionRead the following statements and choose the correct answer.
(a) For a freely falling body the average velocity is proportional to square root of height of fall.
(b) For a freely falling body the displacements in successive equal time intervals are in the ratio 1:4:9:....
(c) For a vertically projected body the displacement during last second of time of flight changes with velocity of projection.
(d) For a body projected from the top of the tower the displacement of the body is negative when the body crosses the point of projection
View Solution
