Assertion : Four point masses each of mass m are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is Gma2
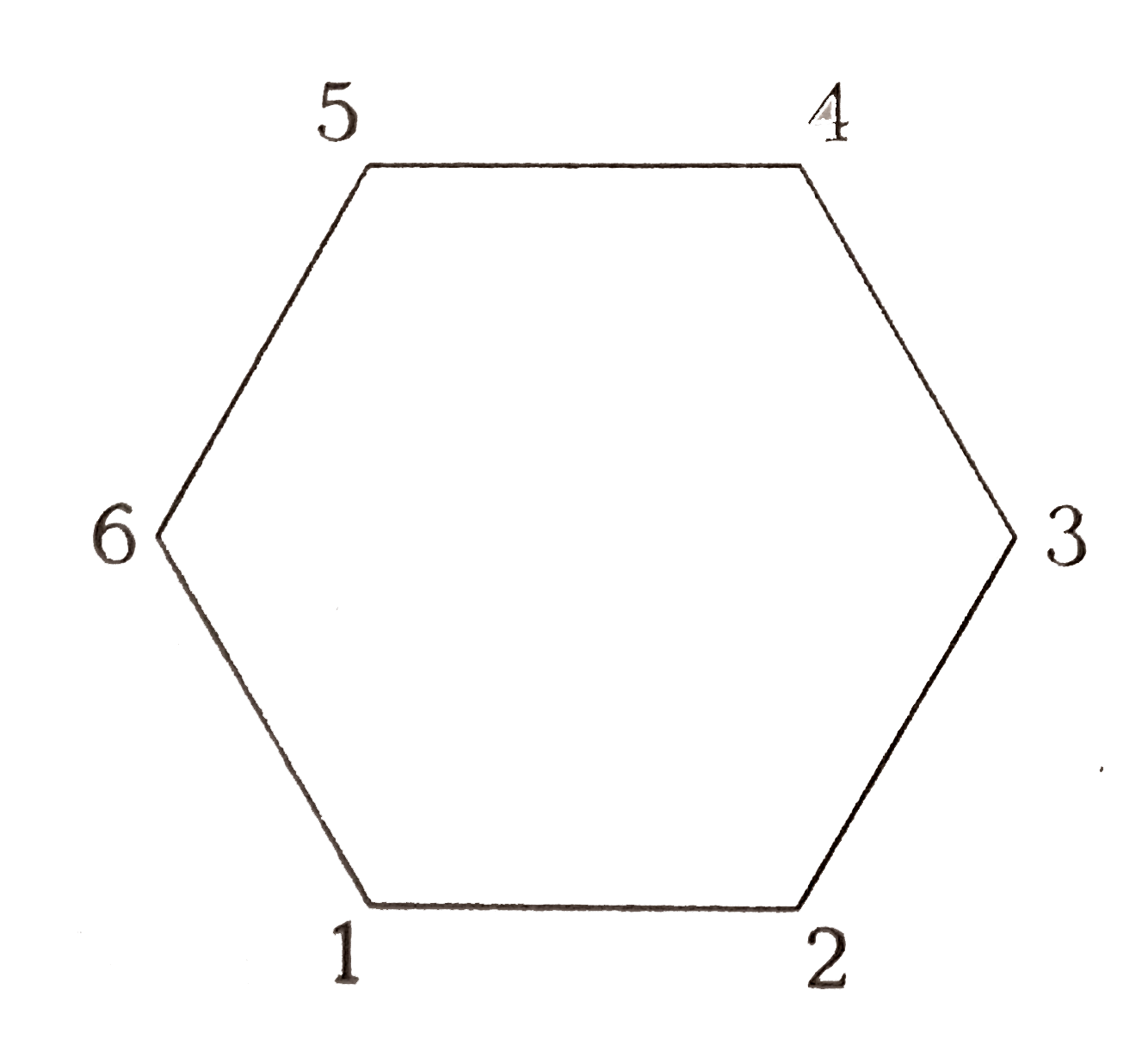
Reason : The field strength due to masses at 3 and 6 are cancelled out.
If both Assertin and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:D
Field strengths due to masses at 1 and 2 are acting at 60∘.
Therefore, resultant is √3Gma2
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
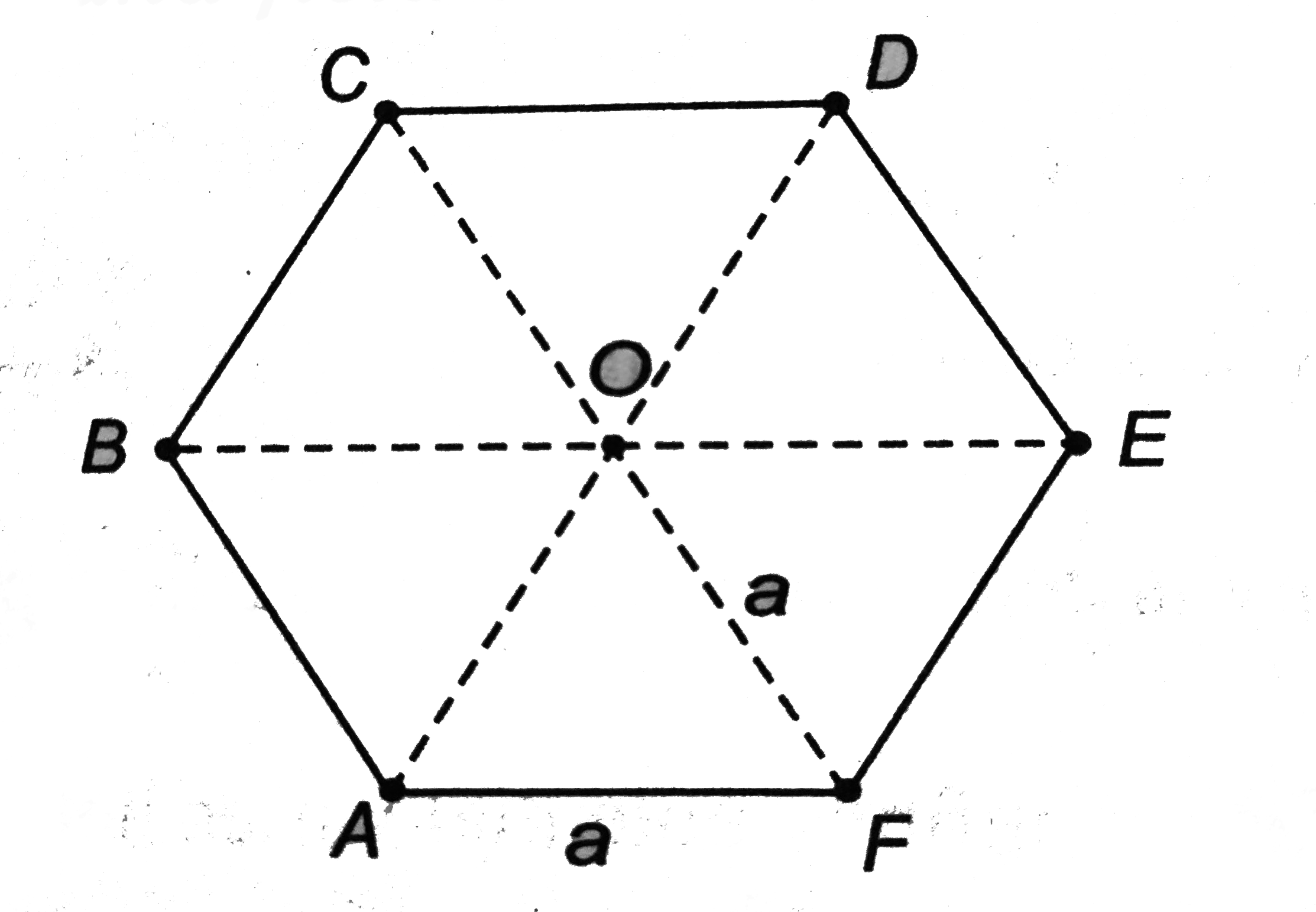
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
 .
.
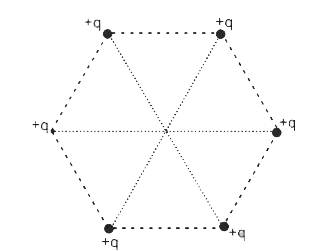
View SolutionSix equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
View Solution
Knowledge Check
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
AzeroB3GML2C9GML2D2GML2Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
AzeroB3GML2C9GML2D12GM√3L2Four point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
AGravitation field at centre at zeroBGravitation potential at centre is −4GmrCGravitation potential energy of system in −6Gm2rDGravitation force on one of the point mass is √6Gm2r2
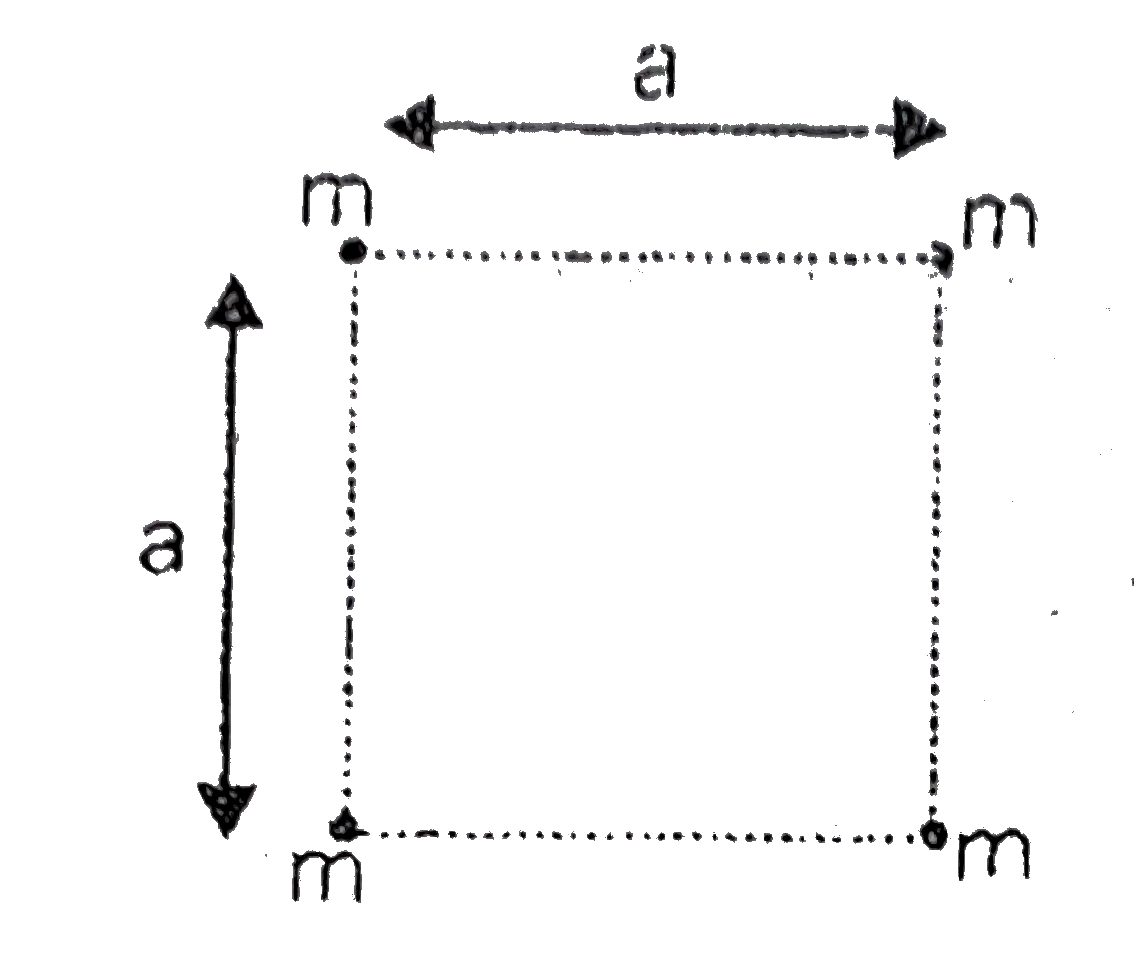
Four point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
 .
.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View Solution
