Assertion:Although the surfaces of goggle lens are curved, It does not have any power.
Reason: In case of goggles, both the curved surfaces have equal radii of curvature and have centre of curvature on the same side.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of the Assertion.
If both Assertion is true, but the Reason is false.
If both Assertion is false but the Reason is true.
The correct Answer is:A
To solve the question, we need to analyze the assertion and the reason provided regarding the goggle lens.
1. Understanding the Assertion:
- The assertion states that although the surfaces of goggle lenses are curved, they do not have any power.
- In optics, the power of a lens is defined as the reciprocal of its focal length (P = 1/f). If a lens has no power, it means its focal length is infinite.
2. Understanding the Reason:
- The reason states that in the case of goggles, both curved surfaces have equal radii of curvature and their centers of curvature are on the same side.
- This suggests that the lens is symmetric and behaves differently than typical converging or diverging lenses.
3. Analyzing the Lens Formula:
- The lens maker's formula is given by:
1f=(μrelative−1)(1r1−1r2)
- For goggle lenses, if both surfaces have equal radii of curvature (let's say r), then:
r1=randr2=−r
- Substituting these values into the lens formula:
1f=(μrelative−1)(1r−1−r)=(μrelative−1)(1r+1r)=2(μrelative−1)1r
4. Determining the Focal Length:
- If the radii are equal and the centers of curvature are on the same side, the effective focal length approaches infinity, leading to:
1f=0⇒f=∞
- Therefore, the power of the lens is:
P=1f=0
5. Conclusion:
- Both the assertion and reason are true. The assertion is correct because the goggle lens does not have any power, and the reason correctly explains why this is the case.
Final Answer:
- Assertion: True
- Reason: True
- The reason is a correct explanation of the assertion.
- The assertion states that although the surfaces of goggle lenses are curved, they do not have any power.
- In optics, the power of a lens is defined as the reciprocal of its focal length (P = 1/f). If a lens has no power, it means its focal length is infinite.
- The reason states that in the case of goggles, both curved surfaces have equal radii of curvature and their centers of curvature are on the same side.
- This suggests that the lens is symmetric and behaves differently than typical converging or diverging lenses.
- The lens maker's formula is given by:
1f=(μrelative−1)(1r1−1r2)
- For goggle lenses, if both surfaces have equal radii of curvature (let's say r), then:
r1=randr2=−r
- Substituting these values into the lens formula:
1f=(μrelative−1)(1r−1−r)=(μrelative−1)(1r+1r)=2(μrelative−1)1r
- If the radii are equal and the centers of curvature are on the same side, the effective focal length approaches infinity, leading to:
1f=0⇒f=∞
- Therefore, the power of the lens is:
P=1f=0
- Both the assertion and reason are true. The assertion is correct because the goggle lens does not have any power, and the reason correctly explains why this is the case.
- Assertion: True
- Reason: True
- The reason is a correct explanation of the assertion.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Objective
38 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.8
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Knowledge Check
Assertion : The focal length of an equiconvex lens placed in air is equal to radius of curvature of either face.
Reason : For an equiconvex lens radius of curvature of both the faces is same.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
A double convex lens has power P and same radii of curvature R of both the surfaces. The radius of carvature of a surface of plano-convex lens made of the same meterial with power 1.5 P is :
View SolutionA double convex lens has two surfaces of equal radii R and refractive index m=1.5, we have
View SolutionGiven figures shows the arrangement of two lenses. The radii of curvature of all the curved surfaces are same. The ratio of the equivalent focal length of combinations P,Q and R is:

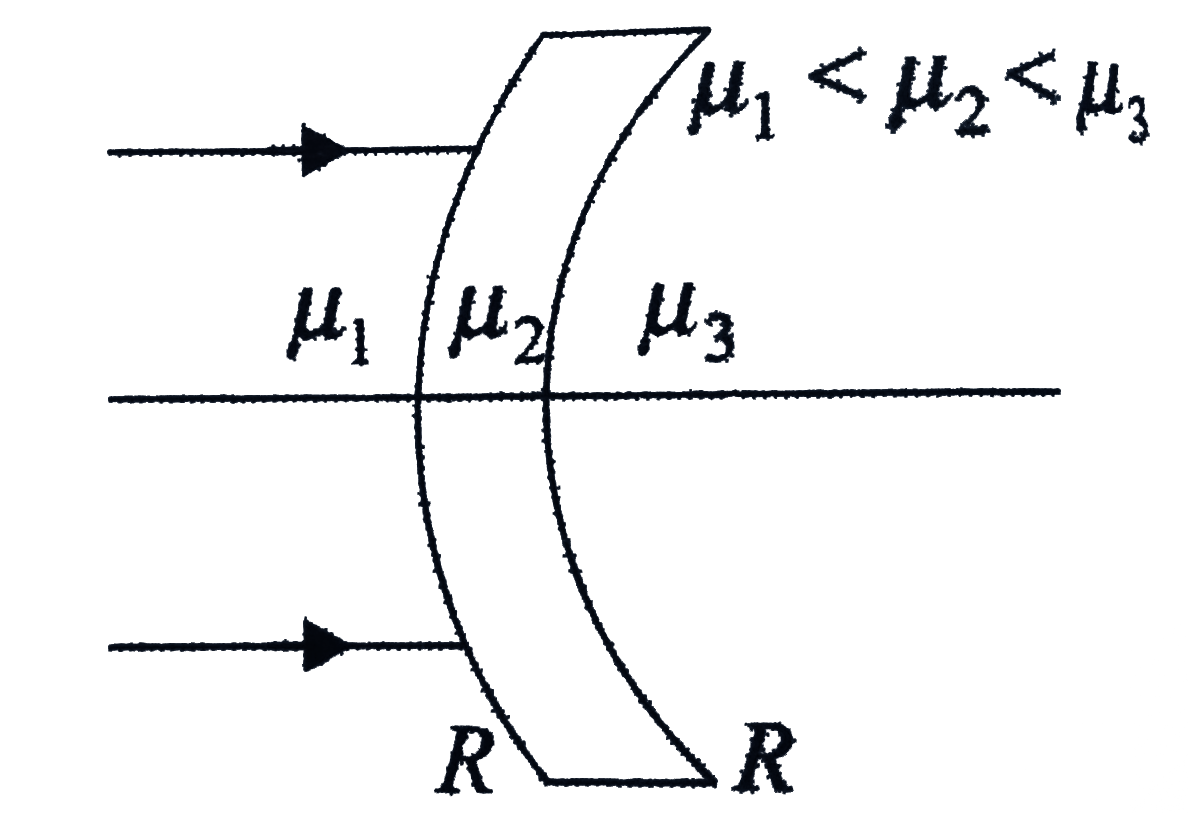
View SolutionThe adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionA point object is places on the principal axis of a thin lens with parallel curved boundaries, i.e., having same radii of curvature. Discuss about the position of the image formed.
View SolutionIn the given diagram find the position where the equivalent lens can be placed for image formation by rays takes place at same place as in the given diagram. Assume that all the curved surfaces have same radii and same optical axis for both the lenses.

View SolutionThe surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
View Solution