A double convex lens has two surfaces of equal radii R and refractive index m=1.5, we have
f=R2
f=R
f=−R
f=2R
The correct Answer is:B
To solve the problem regarding a double convex lens with equal radii R and a refractive index μ=1.5, we will use the lens maker's formula. The lens maker's formula is given by:
1f=(μ−1)(1R1−1R2)
Step 1: Identify the radii of curvature
For a double convex lens:
- The radius of curvature of the first surface, R1, is positive: R1=+R
- The radius of curvature of the second surface, R2, is negative: R2=−R
Step 2: Substitute the values into the lens maker's formula
Substituting R1 and R2 into the lens maker's formula:
1f=(μ−1)(1R−1−R)
Step 3: Simplify the equation
Calculating 1R−1−R:
1R−1−R=1R+1R=2R
Now substituting this back into the equation:
1f=(1.5−1)(2R)
Step 4: Calculate the focal length
Now, simplifying further:
1f=0.5⋅2R=1R
Thus, we find:
f=R
Conclusion
The focal length f of the double convex lens is equal to the radius of curvature R.
---
For a double convex lens:
- The radius of curvature of the first surface, R1, is positive: R1=+R
- The radius of curvature of the second surface, R2, is negative: R2=−R
Substituting R1 and R2 into the lens maker's formula:
Calculating 1R−1−R:
Now, simplifying further:
The focal length f of the double convex lens is equal to the radius of curvature R.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercises
78 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
The radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View Solution
Knowledge Check
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.
A double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View SolutionA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View SolutionIf the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
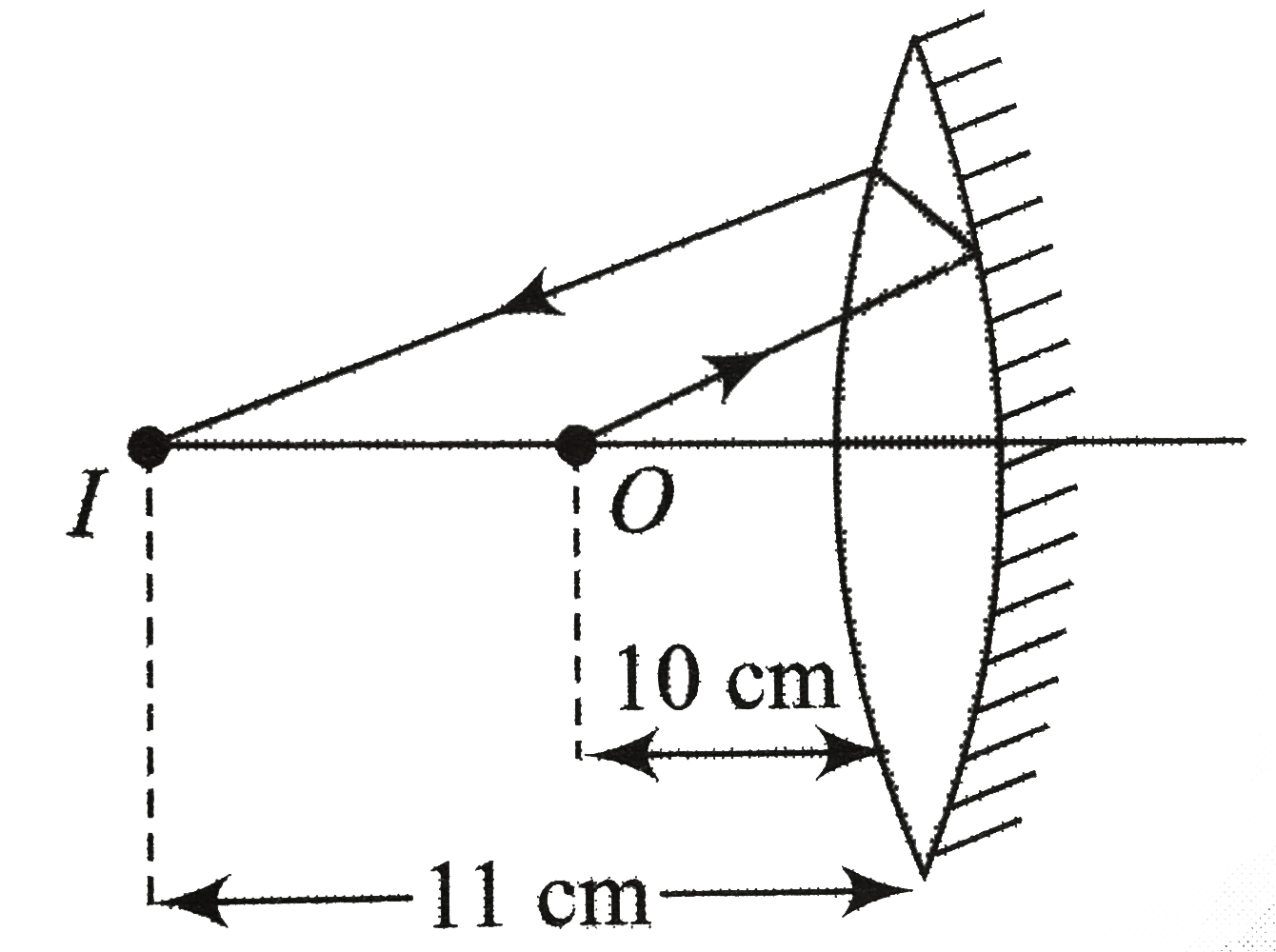
View SolutionA pin is placed 10cm in front of a convex lens of focal length 20cm, made of a material having refractive index 1.5 . The surface of lens farther away from the pin is silvered and has a radius of curvature 22cm. Determine the position of the final image. Is the image real or virtual?
View SolutionA double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is :
View SolutionAn object in placed 30cm in front of a concave lens that is made of a glass of refractive index 1.5 and has equal radii of curvature of its two surfaces, each 30 cm. The surface of the lens farther away from the object is silvered. Find the nature and position of the final image.
View Solution
