Average life ofa radioactive sample is 4 ms Initially the total number of nuclie is N0 A charged capacitor of capacity 20μf is connected across a resistor R. The value of R such that ratio of number of nuclei remaining to the charge on capacitor remains constant with time is
100Ω
200Ω
300Ω
400Ω
The correct Answer is:B
To solve the problem, we need to find the value of the resistor R such that the ratio of the number of radioactive nuclei remaining to the charge on the capacitor remains constant over time.
1. Understanding the Decay of Radioactive Nuclei:
The number of radioactive nuclei remaining at time t can be expressed using the formula:
N(t)=N0e−λt
where N0 is the initial number of nuclei and λ is the decay constant.
2. Charge on the Capacitor:
The charge Q(t) on the capacitor at time t can be expressed as:
Q(t)=Q0e−tRC
where Q0 is the initial charge on the capacitor, R is the resistance, and C is the capacitance.
3. Setting Up the Ratio:
We need to find R such that the ratio N(t)Q(t) remains constant over time:
N(t)Q(t)=N0e−λtQ0e−tRC
4. Simplifying the Ratio:
This simplifies to:
N(t)Q(t)=N0Q0e−(λ−1RC)t
For the ratio to remain constant, the exponent must equal zero:
λ−1RC=0
Thus, we have:
λ=1RC
5. Finding the Decay Constant λ:
The average life T of the radioactive sample is related to the decay constant by:
T=1λ
Given that the average life T=4ms=4×10−3s, we can find λ:
λ=1T=14×10−3=250s−1
6. Substituting Values:
Now substituting λ into the equation λ=1RC:
250=1R×20×10−6
7. Solving for R:
Rearranging gives:
R=1250×20×10−6=15×10−3=200Ω
Final Answer:
The value of R such that the ratio of the number of nuclei remaining to the charge on the capacitor remains constant with time is:
R=200Ω
The number of radioactive nuclei remaining at time t can be expressed using the formula:
N(t)=N0e−λt
where N0 is the initial number of nuclei and λ is the decay constant.
The charge Q(t) on the capacitor at time t can be expressed as:
Q(t)=Q0e−tRC
where Q0 is the initial charge on the capacitor, R is the resistance, and C is the capacitance.
We need to find R such that the ratio N(t)Q(t) remains constant over time:
N(t)Q(t)=N0e−λtQ0e−tRC
This simplifies to:
N(t)Q(t)=N0Q0e−(λ−1RC)t
For the ratio to remain constant, the exponent must equal zero:
λ−1RC=0
Thus, we have:
λ=1RC
The average life T of the radioactive sample is related to the decay constant by:
T=1λ
Given that the average life T=4ms=4×10−3s, we can find λ:
λ=1T=14×10−3=250s−1
Now substituting λ into the equation λ=1RC:
250=1R×20×10−6
Rearranging gives:
R=1250×20×10−6=15×10−3=200Ω
The value of R such that the ratio of the number of nuclei remaining to the charge on the capacitor remains constant with time is:
R=200Ω
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
A radioactive sample decays with an average life of 20ms. A capacitor of capacitance 100μF is charged to some potential and then the plates are connected through a resistance R. What should be the value of R so that the ratio of the charge on the capacitor to the activity of the radioactive sample remains constant in time?
View SolutionA radioactive sample decays with a mean life of 20ms. A capacitor of capacitance 100μF is charged to some potential and then the plates are connected to a resistance .R.. If the ratio of the charge on the capacitance to the activity of radioactive sample remains constant in time is R=100(x)Ω, then x=
View SolutionA capacitor given a charge Q0 is conected across a resistor R at t = 0. The separation between the plates changes according to d=d(1+t)(0≤t<1) Find the variation of charge on capacitor with time.

View SolutionThe plates of a 50(μ)F capacitor charged to 400(μ)C are connected through a resistance of 1.0k(ohm). Find the charge remaining on the capacitor 1s after the connection is made.
View SolutionA 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionIn the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L. A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t=0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod (cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)
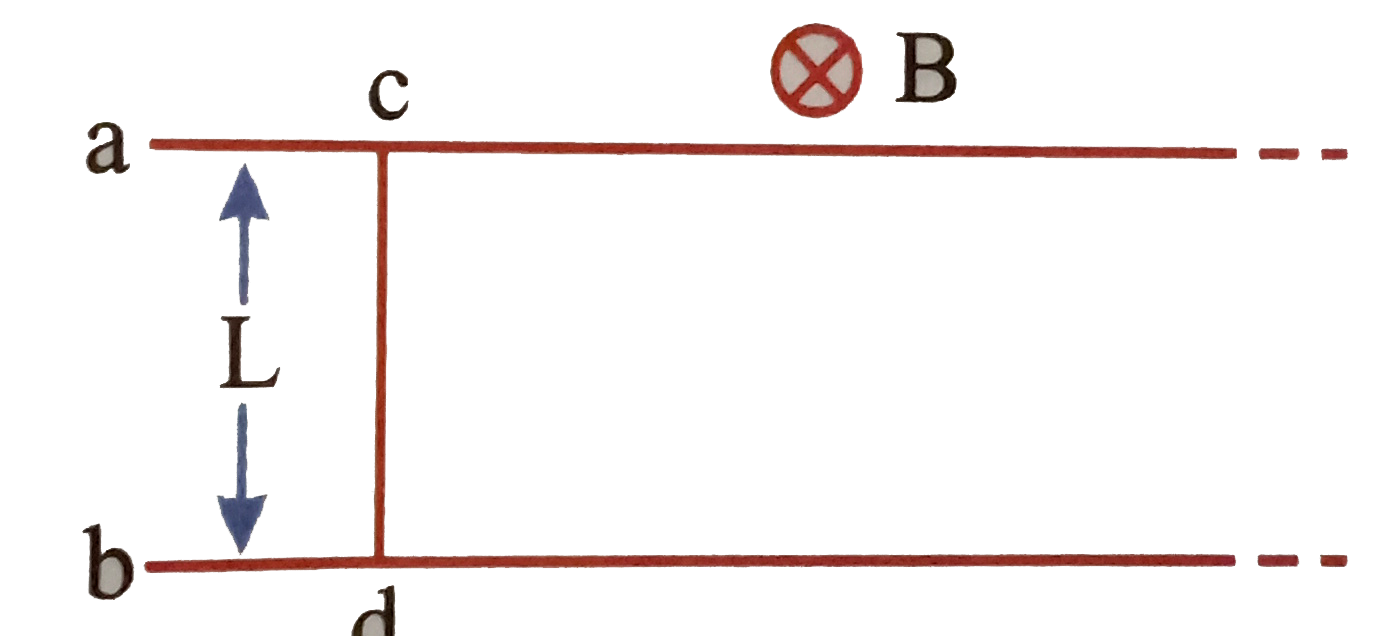
When the speed of rod is v, the charge on capacitor is :
View SolutionA charged capacitor of capacitance C is discharged through a resistance R. A radioactive sample decays with an average-life τ.Find the value of R for which the ratio of the electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant in time.
View SolutionA inductor of inductance L is decayed through a resistance R. A radioactive sample decays with an average life T. The value of R for which the electric energy stored in the inductor to the activity of radioactive sample remains constant
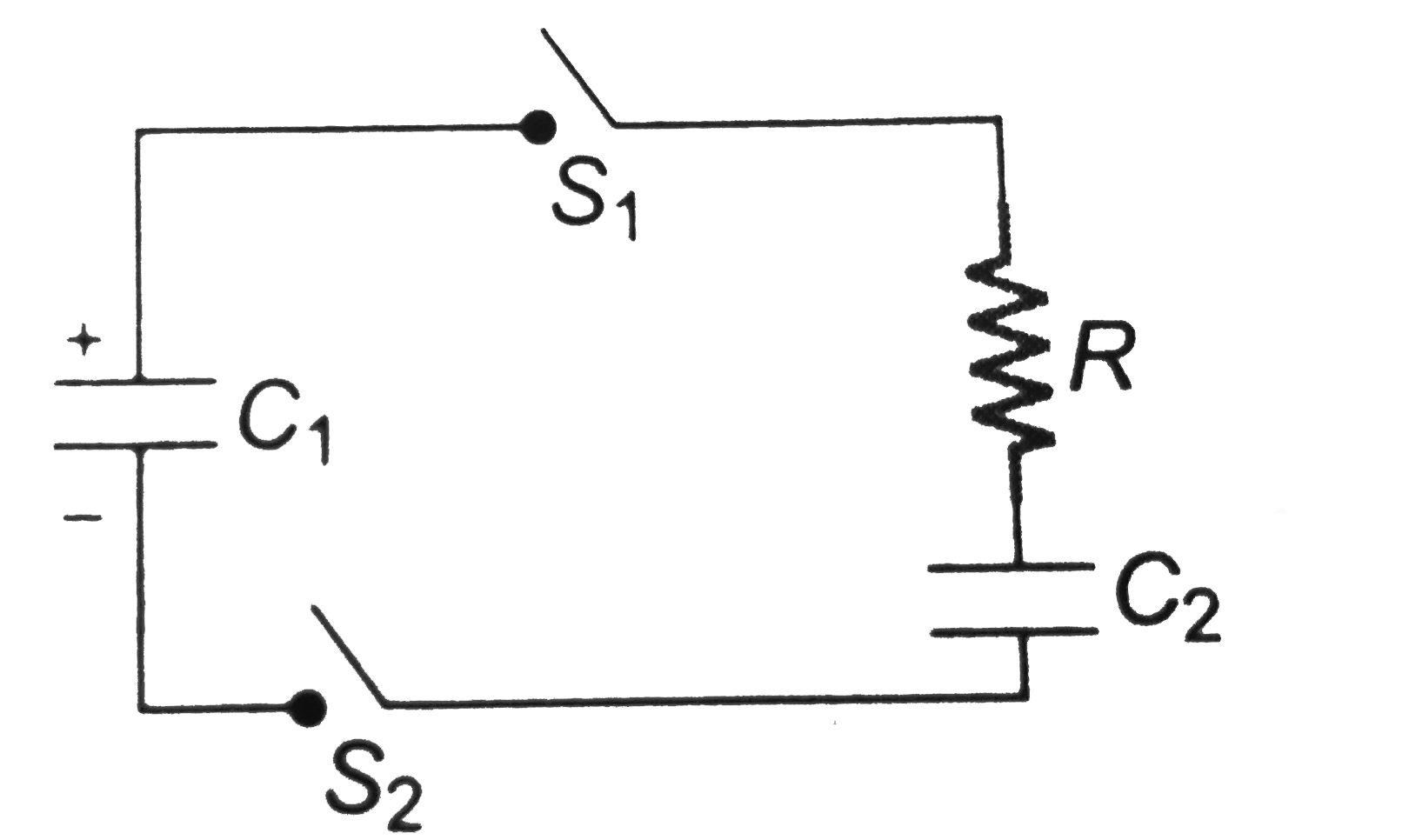
View SolutionThe capactor C1 in the figure initially carries a charge q0. When the i switch S1 and S2 are closed, capacitor C1 is connected to a resistor R and a second capacitor C2, which initially does not carry any charge.
(a) Find the charges deposited on the capacitors in steady state and the current through R as a function of time.
(b) What is heat lost in the resistor after a long time of closing the switch?
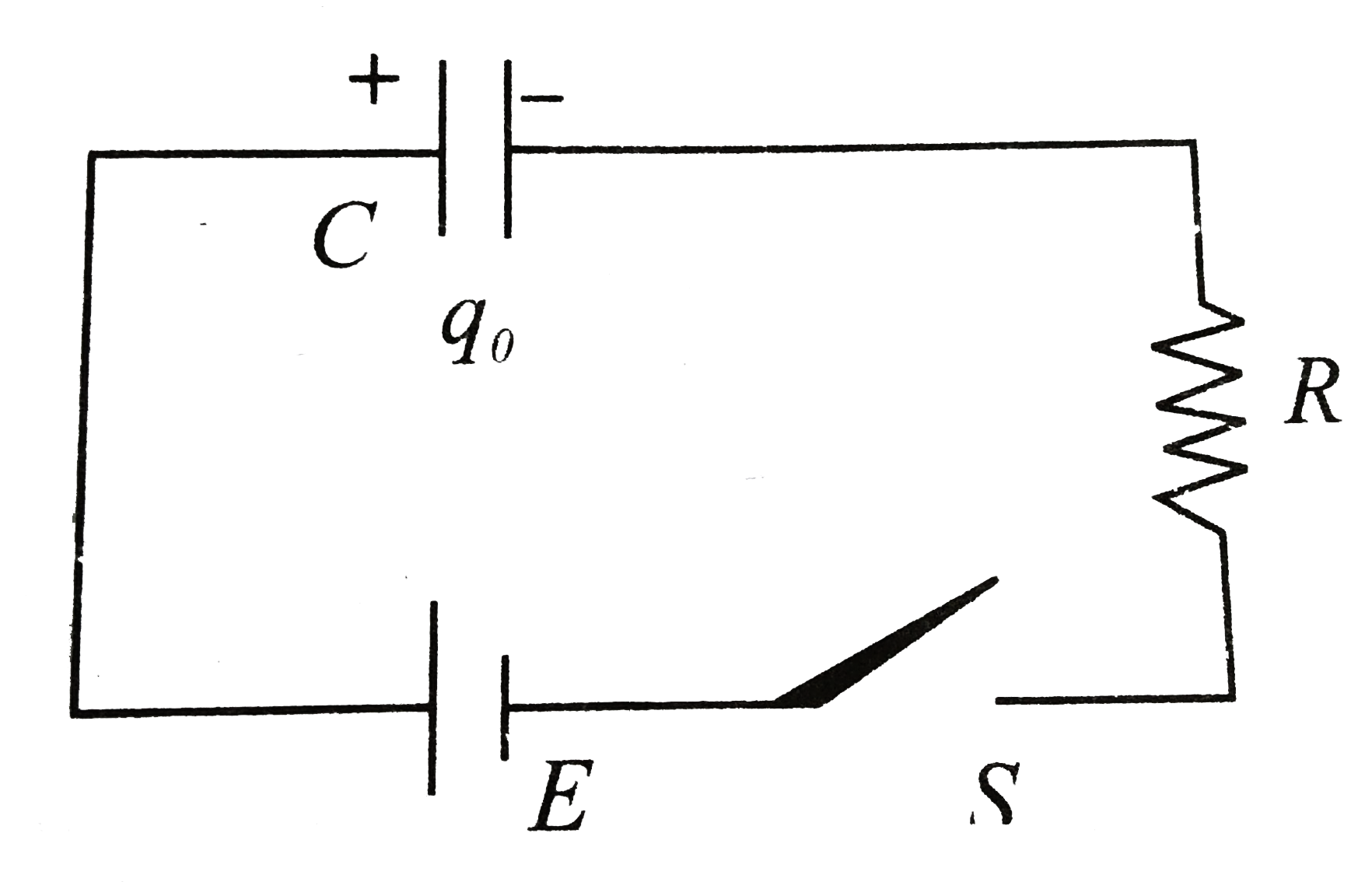
View SolutionA capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
View Solution
