Calculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent $γ$ .
(a) increased $n - f o l d$ ,
(b) decreases $n - f o l d$ .

Video Solution

Text Solution

Verified by Experts

(a) $Q'_{2} = C_{p} T_{0} (1 - \frac{1}{n}), Q''_{1} = R T_{0} 1 n n, Q'_{1} = C_{V} T_{0} (1 - \frac{1}{n}), Q_{1} = Q'_{1} + Q''_{1}$
So $η = 1 - \frac{Q'_{2}}{Q_{1}} = 1 - \frac{C_{p} (1 - \frac{1}{n})}{C_{V} (1 - \frac{1}{n}) + R 1 n n}$
= $1 - \frac{γ}{1 + \frac{R}{C_{V}} \frac{n 1 n n}{n - 1}} = 1 - \frac{γ (n - 1)}{n - 1 + (γ - 1) n 1 n n}$
(b) $Q_{1} = C_{p} T_{0} (n - 1), Q''_{2} = C_{V} T_{0} (n - 1) Q'''_{2} = R T_{0} 1 n n, Q'_{2} = Q''_{2} + Q'''_{2}$
So $η = 1 - \frac{Q'_{2}}{Q_{1}} = 1 - \frac{n - 1 + (γ - 1) 1 n n}{γ (n - 1)}$ .

Updated on:21/07/2023

In an isothermal process the volume of an ideal gas is halved. One can say that
AInternal energy of the system decreases
BWork done by the gas is positive
CWork done by the gas is negative
DInternal energy of the system increases
The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

A $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$
B $\frac{(1 - 2 ln 2)}{γ / (γ - 1)}$
C $\frac{(2 ln 2 + 1)}{γ / (γ - 1)}$
D $\frac{(2 ln 2 - 1)}{γ / (γ + 1)}$
The efficiency of an ideal gas with adiabatic exponent $' γ'$ for the shown cyclic process would be

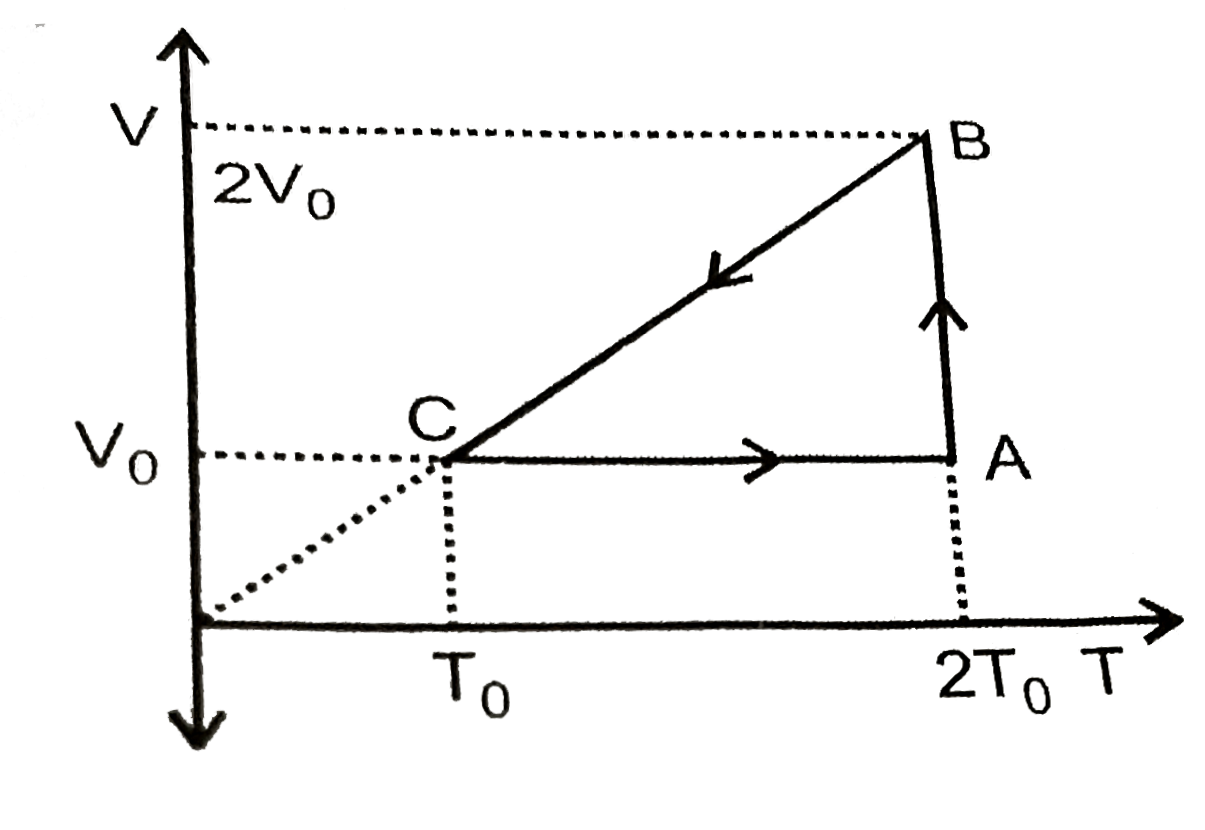A $\frac{(γ - 1) (2 ln 2 - 1)}{1 + (γ - 1) 2 ln 2}$
B $\frac{(γ - 1) (1 - 2 ln 2)}{(γ - 1) 2 ln 2 - 1}$
C $\frac{(2 ln 2 + 1) (γ - 1)}{(γ - 1) 2 ln 2 + 1}$
D $\frac{(2 ln 2 - 1)}{γ / (γ - 1)}$