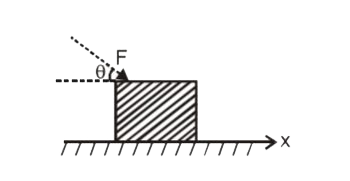
Calculate the minimum force required to drag a body of mass m, resting on a horizontal surface. The coefficient of friction between the body and the surface is μ.
Let the applied force be F, acting at an angle θ with the horizontal Fig.
f2 = force of limiting friction, mg = weight of the body and R = normal force.
For equilibrium,
R+Fsinθ=mg or, R = mg - F sinθ
and F cos θ=fs=μR=μ(mg−Fsinθ)
or, F cos θ+μFsinθ=μmg
∴F=μmgcosθ+μsinθ
Value of F will be minimum when ( cosθ+μsinθ) is maximum.
∴ddθ(cosθ+μsinθ)=0
or , - sin θ+μcosθ=0 or,tanθ=μ
∴sinθ=μ√1+μ2,and cosθ=1√1+μ2
∴Fmin=μmg1√1+μ2+μ2√1+μ2=μmg√1+μ2 andθ=tan−1μ

Topper's Solved these Questions
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - Section Related Questions
9 Videos
- FRICTION BOOK - CHHAYA PUBLICATIONCHAPTER - FRICTION EXERCISE - HIGHER ORDER THINKING SKILL ( HOTS ) QUESTIONS
14 Videos
- FIRST AND SECOND LAW OF THERMODYNAMICSBOOK - CHHAYA PUBLICATIONCHAPTER - FIRST AND SECOND LAW OF THERMODYNAMICSEXERCISE - CBSE SCANNER
18 Videos
- HYDROSTATICSBOOK - CHHAYA PUBLICATIONCHAPTER - HYDROSTATICSEXERCISE - CBSE SCANNER
1 Videos
Similar Questions
Find the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View Solution
Knowledge Check
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2]A force F accelerates a block of mass m on horizontal surface. The coefficient of friction between the contact surface is . The acceleration of m will be -
AF−μmgMBzeroCmay be (A) or (B)DNone of theseA body of mass M is applying horizontal force to slide a box of mass M1 on a rough horizontal surface The coefficient of friction between the shoe of the boy and the floor is μ and that between the box and the floor is 'μ1' In which of the following cases is it certainly not possible to slide the box ? .
Aμ<μ1,M<M1Bμ>μ1,M>M1Cμ<μ1,M>M1Dμ1>μ1,M<M1
A block having a mass 3kg is initially at rest on a horizontal surface. The coefficient of static friction μs=0.3 between theblock and the surface and μk is 0.25 .A constant force F of 50 N, acts on the body at the angle θ=37∘. What is the acceleration of the block ?
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA horizontal force is applied on a body on a rough horizontal surface produces an acceleration ‘a’. If coefficient of friction between the body and surface which is μ is reduced to μ/3, the acceleration increases by 2 units. The value of 'μ' is
View SolutionA horizontal force is applied on a body on a rough horizontal surface produces an acceleration a.If coefficient of friction between the body and surface which is a is reduced to μ/3,the acceleration increses by 2units.The value of μ is
View SolutionA body of mass m, having momentum p, is moving on a rough horizontal surface. If it is stopped in a distance x, the coefficient of friction between the body and the surface is given by
View Solution
