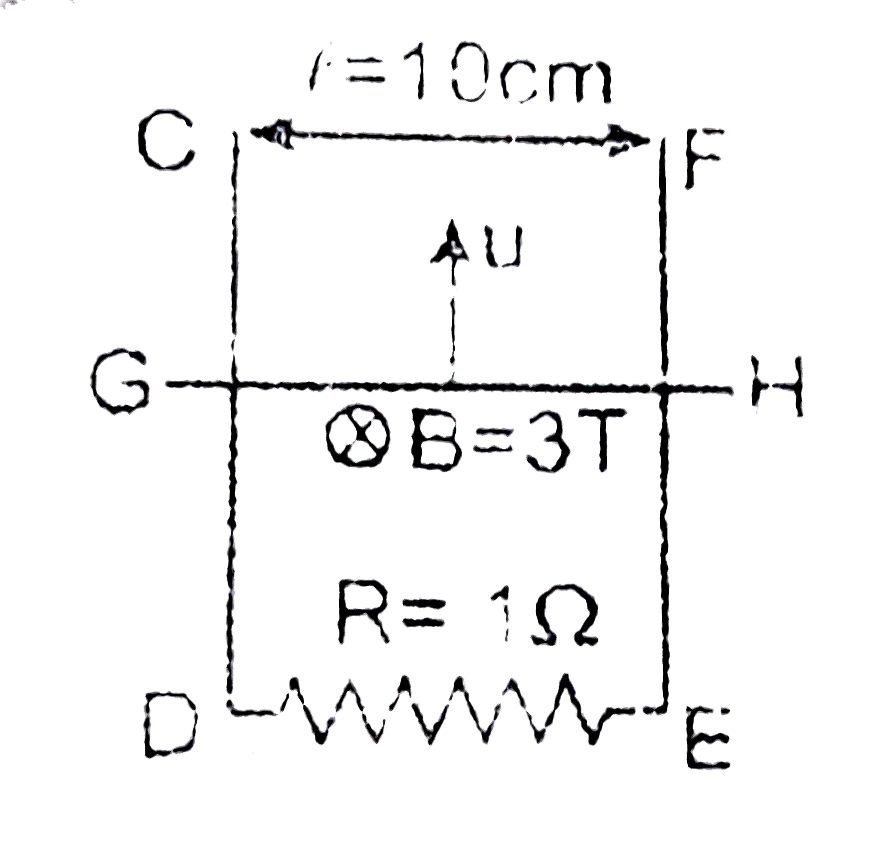
CDEF is a fixed conducting smooth frame in vertical plane. A conducting uniform rod GH of mass m can move vertically and smoothly without losing contact with the frame. Gh always remains horizontal and is given velocity u upward and released. Taking the acceleration due to gravity as g and present other than R. Find out the time tasken by the rod to reach the highest point.

The correct Answer is:mRB2l21n(mgR+B2l2umgR)
Let v be the speed of the rod at any time. Then the equivalent and free body diagrams of rod are shown in . Applying Newton's second law to the rod,
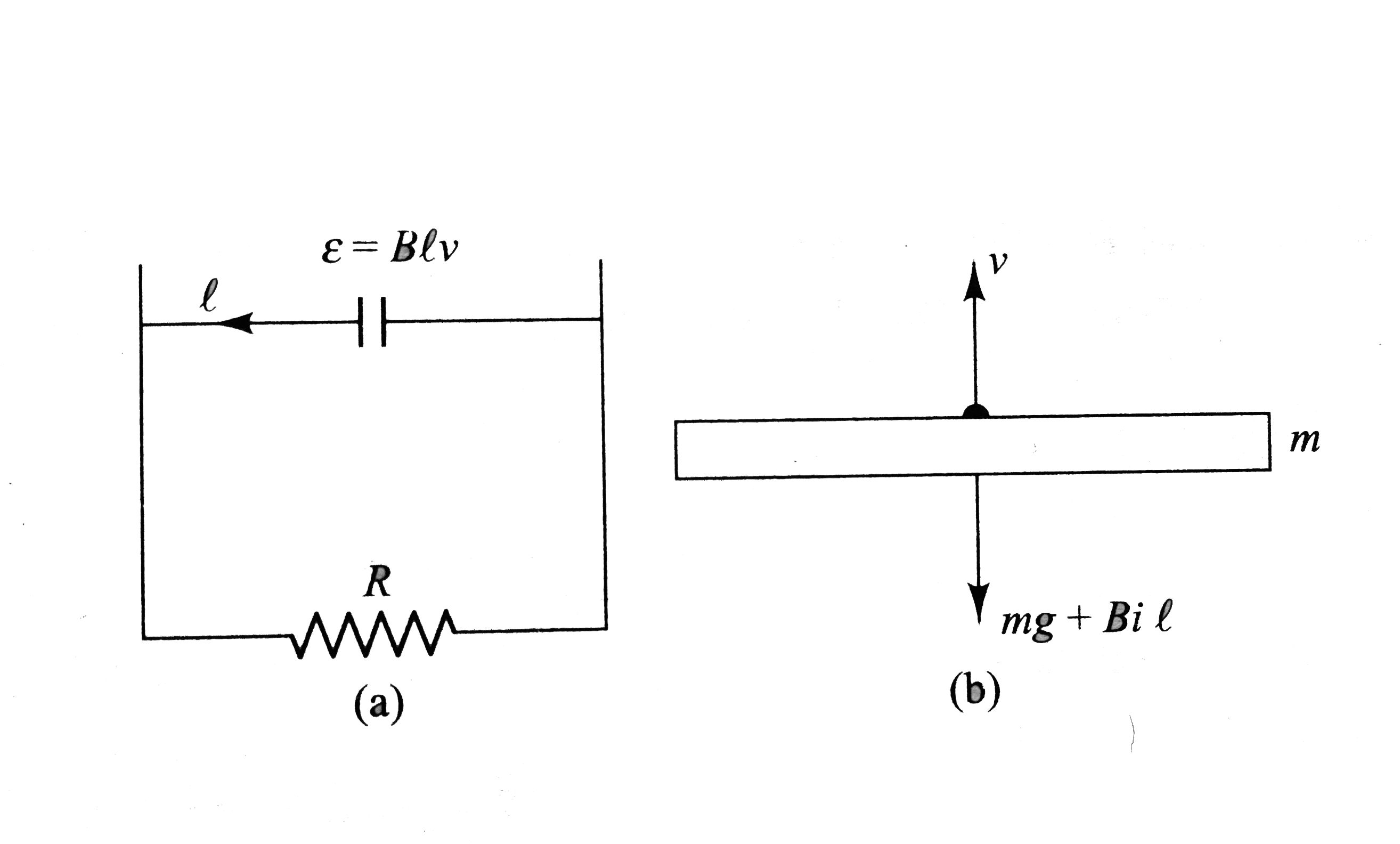 ,
, 
mdvdt=−(mg+Bil)
where i=BlvR
From equation (i) and (ii)
mdvdt=−(mg+B2l2v2R)
Integrating over proper limits we get,
∫0umdvmg+B2l2vR=∫t0−dt
→ t=mRB2l21n(mgR+B2l2umgR)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Multiple Correct
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.2
27 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
In the figure, CDEF is a fixed conducting smooth frame in vertical plane.A conducting uniform rod GH of mass m=1g can move vertically and smoothly without losing contact with the frame.GH always remains horizontal.It is given velocity u=1m/s upwards and released.Taking the acceleration due to gravity as g and assuming that no resistance is present other than R.Time taken by rod to reach the highest point is equal to ln10x second.Find out value of x.
View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
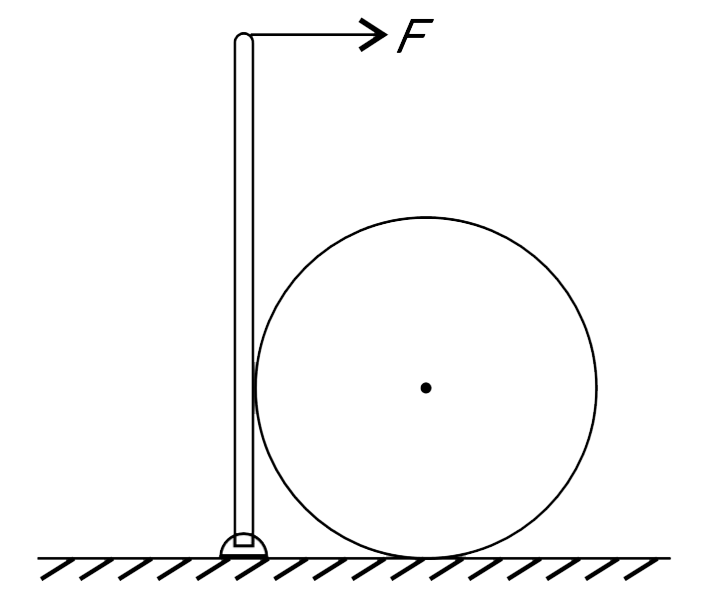
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.
View SolutionRead the given passage and answer the following questions.
A body is thrown vertically up with a velocity u as shown in the figure. It passes through points P and Q in its upward journey and reaches the maximum height at point R. Here PQPR=716,OP=2u245 , and take g=10m/s2
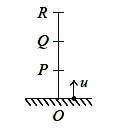
Find the time taken by the particle to reach highest point R.
View SolutionA conducting frame abcd is kept in a vertical plane. A conducting rod of of mass m and length l can slide smoothly on it remaining always horizontal. The resistance of the loop is negligible and inductance is constant having value L. The rod is left from rest and allowed to fall under gravity and inductor has no initial current. A magnetic field of constant magnitude Bis present throughout the loop pointing inwards. Determine

(a) position of the rod as a function of time assuming initial position of the rod to be x=0 and vertically downward as the positive x-axis.
(b) the maximum current in the circuit.
(c) maximum velocity of the rod
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
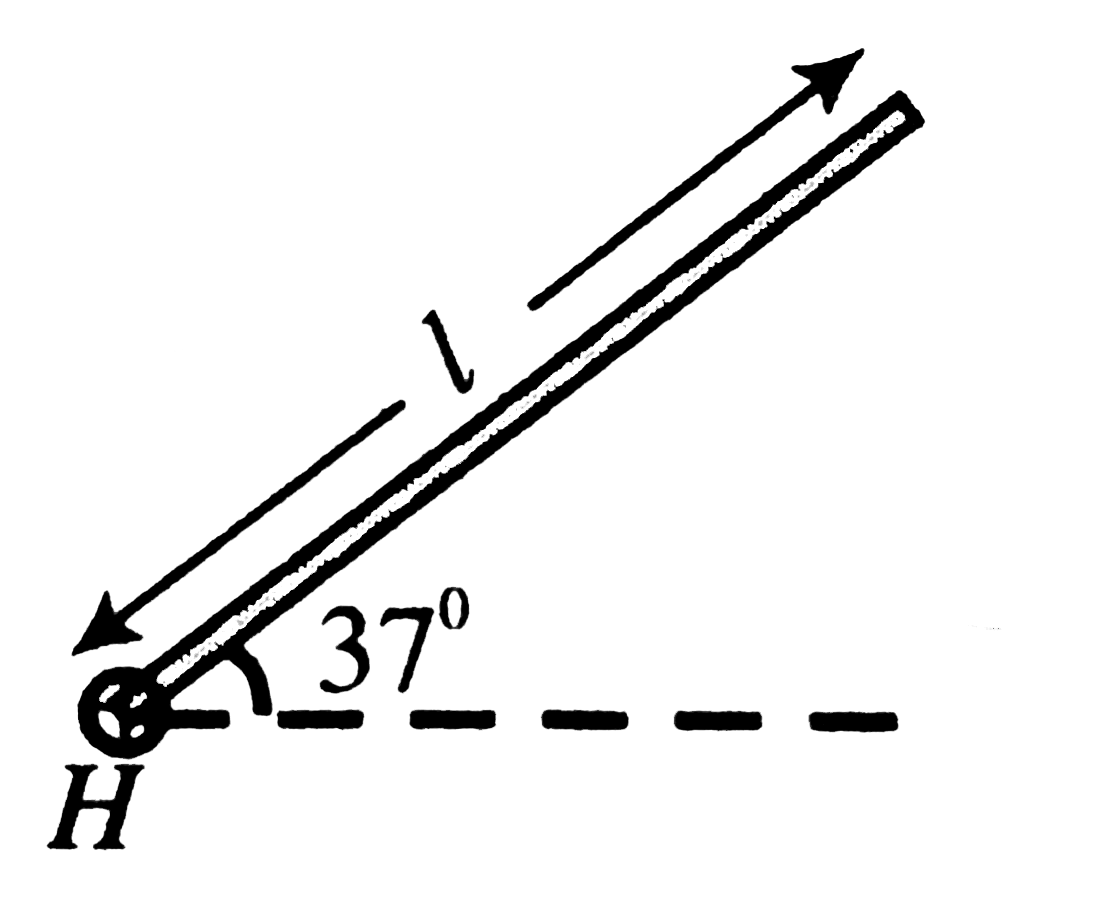
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

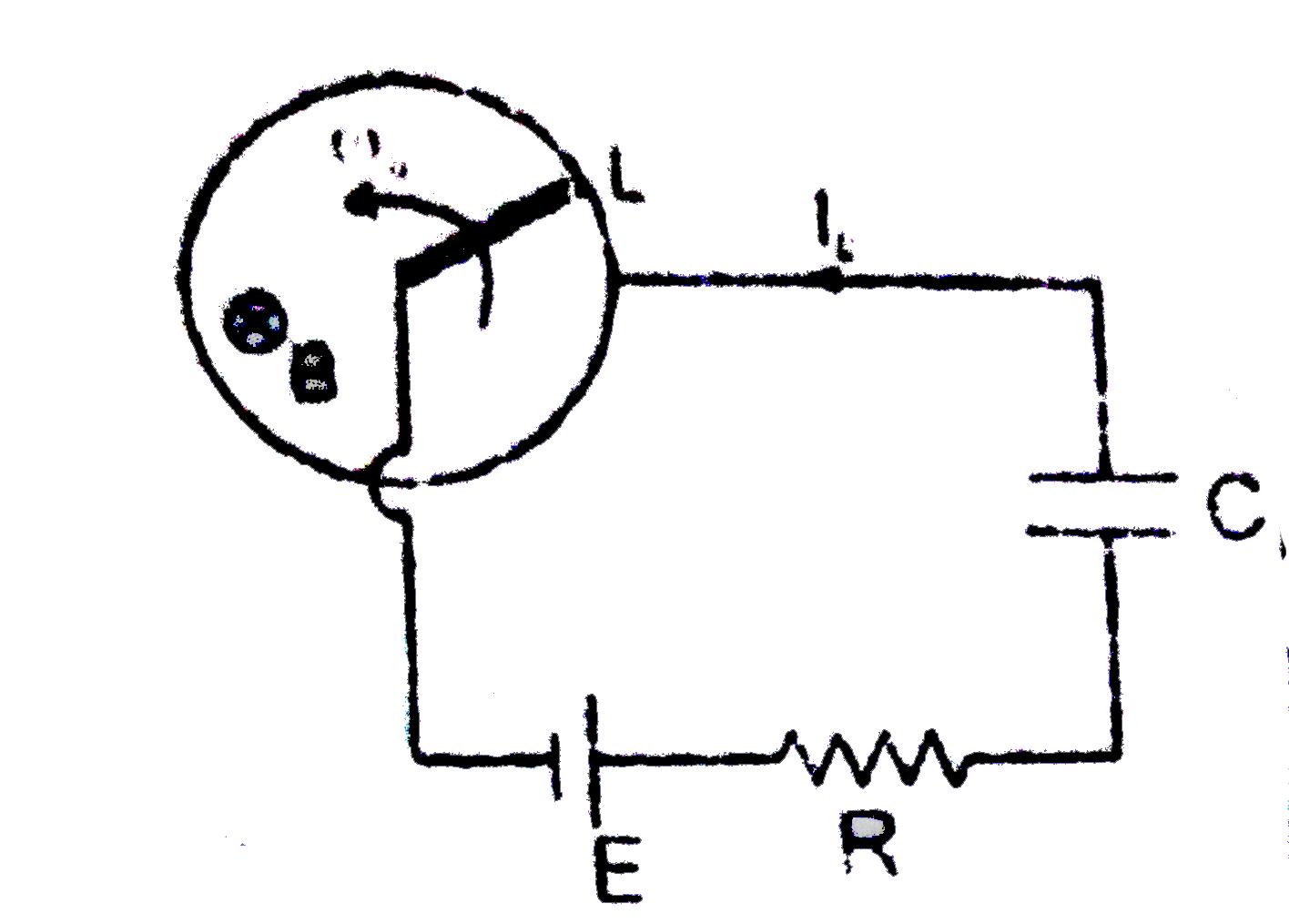
View SolutionL is a smooth conducting loop of radius l=1.0m & fixed in a horizontal plane.A conducting rod of mass m=1.0kg and length slightly greater than l higed at the centre of the loop can rotate in the horizontal plane such that the free end slides on the rim of the loop.There is a uniform magnetic field of strength B=1.0T directed vertically downward.The rod is rotated with angular velocity ω0=1.0rad/s and left.The fixed end of the rod and the rim of the loop are connected through a battery of e.m.f E a resistance R=1Ω, and initially uncharged capacitor of capacitance C=1.0F in series.Find
(i)the time dependence of e.m.f M such that the current I0=1.0A in the circuit is contant.
(ii)energy supplied by the battery by the time rod stops.
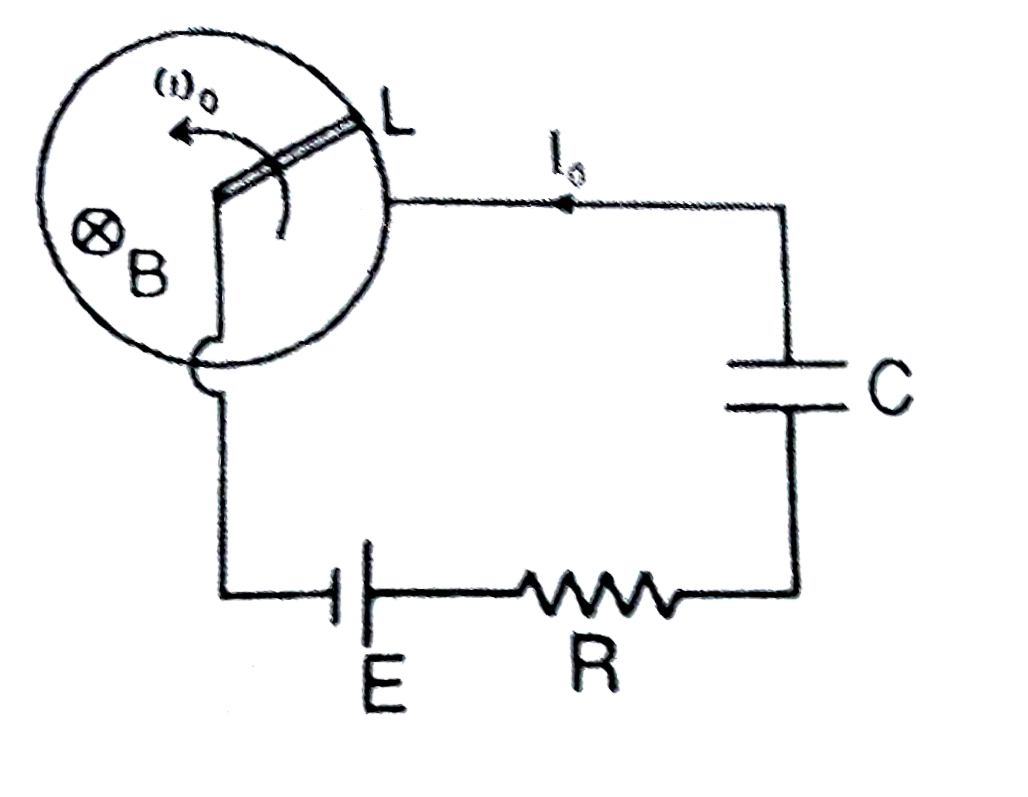
View SolutionL is a smooth conducting loop of radius l=1.0 m & fixed in a horizontal plane. A conducting rod of mass m=1.0 kg and length slightly greater than l hinged at the centre of the loop can rotate in the horizontal plane such that the free end slide on the rim of the loop. There is a uniform magnetic field of strength B=1.0 T directed vertically downward. The rod is rotated with angular velocity ω0=1.0rad/s and left. The fixed end of the rod and the rim of the loop are connected through a battery of emf . E, a resistor of resistance R=1.0Ω, and intially uncharged capacitor of capacitance C=1.0 F in series. Find :
(i) the time dependence of emf . E such that the current I0=1.0A in the circuit is constant.
(ii) energy supplied by the battery by the time rod stops.
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
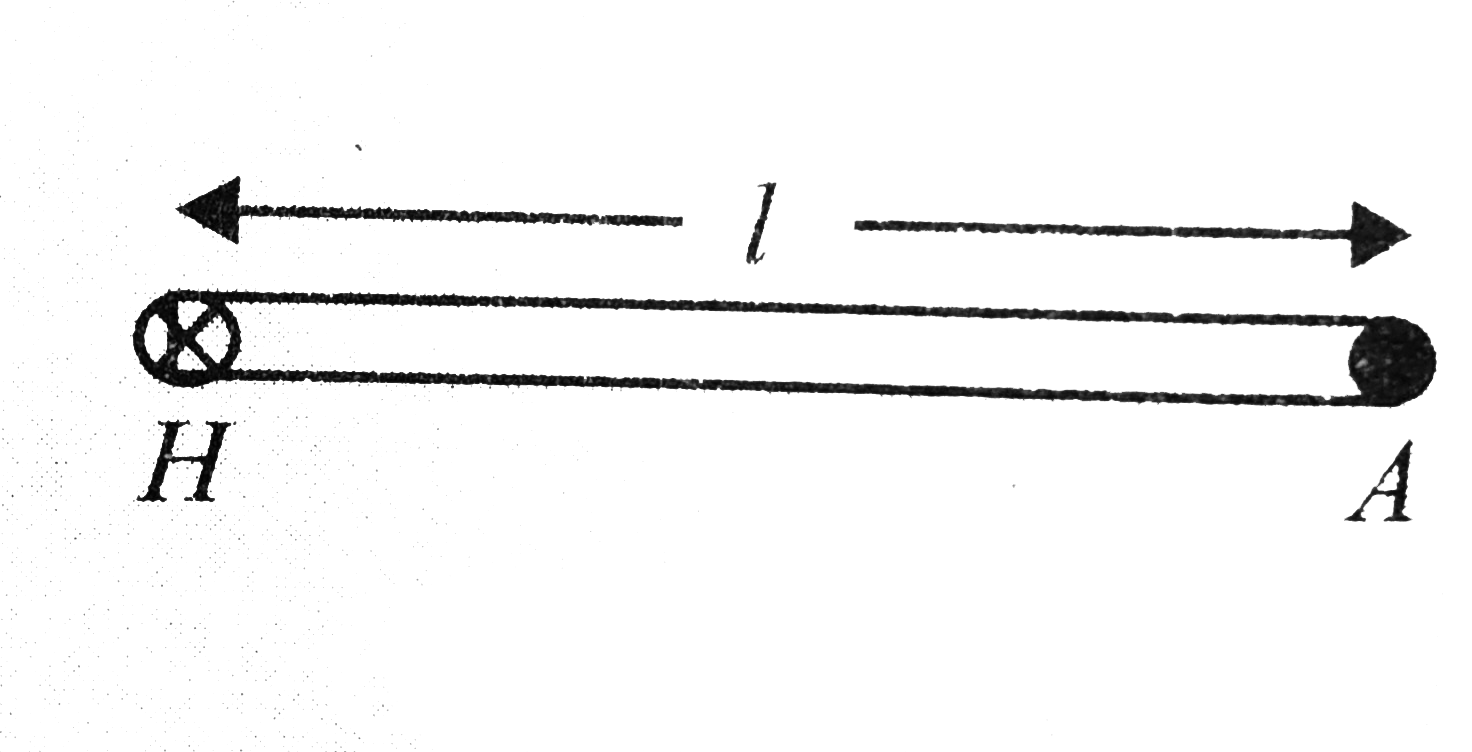
View SolutionA uniform rod of mass m and length l can rotate freely on a smooth horizontal plane about a vertical axis hinged at point H. A point mass having same mass m coming with an initial speed u perpendicular to the rod, strikes the rod in-elastically at its free end. Find out the angular velocity of the rod just after collision?

View Solution
