A conducting frame abcd is kept in a vertical plane. A conducting rod of of mass m and length can slide smoothly on it remaining always horizontal. The resistance of the loop is negligible and inductance is constant having value . The rod is left from rest and allowed to fall under gravity and inductor has no initial current. A magnetic field of constant magnitude Bis present throughout the loop pointing inwards. Determine
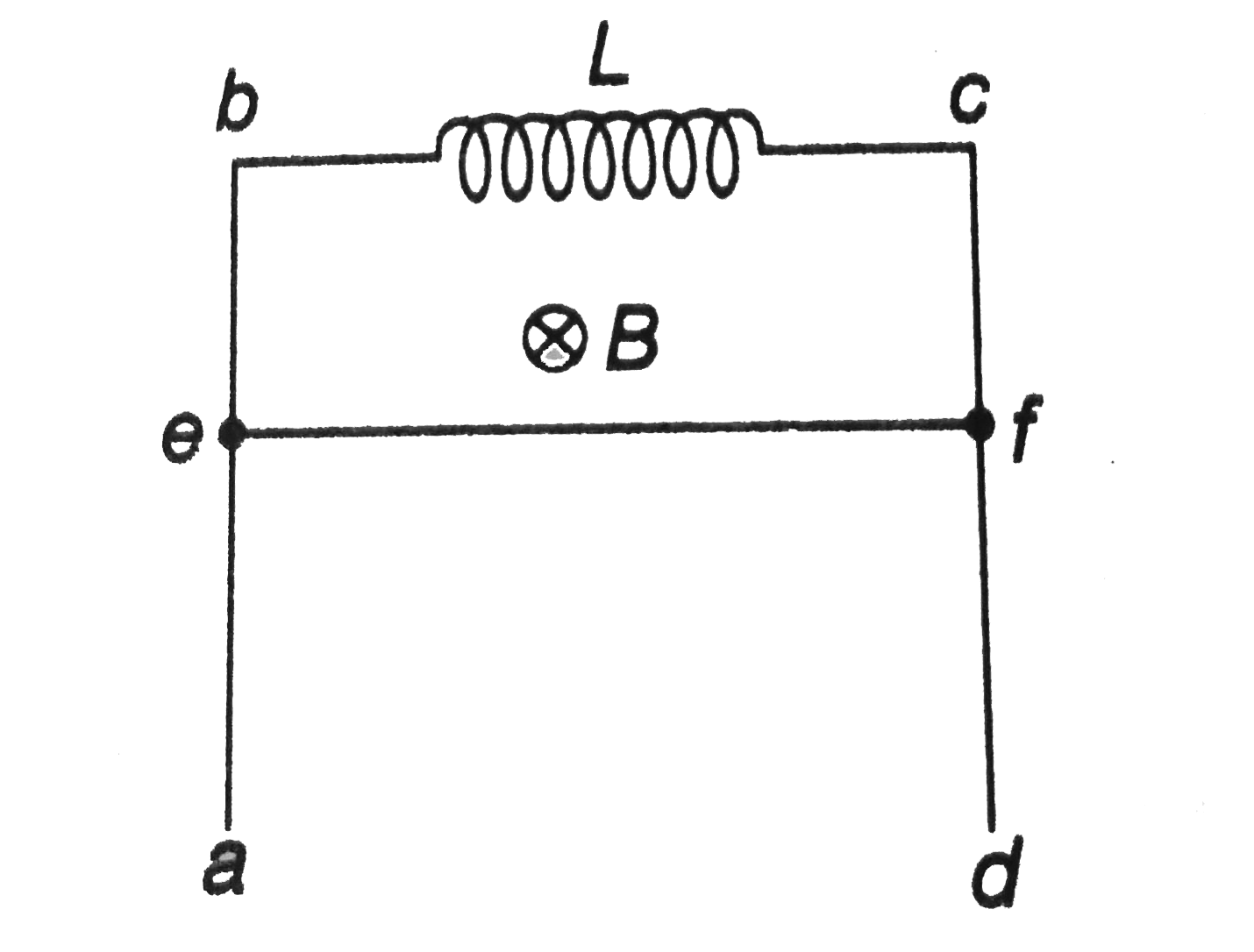
(a) position of the rod as a function of time assuming initial position of the rod to be and vertically downward as the positive x-axis.
(b) the maximum current in the circuit.
(c) maximum velocity of the rod
The correct Answer is:B
a. Suppose be the velocity of rod whenit has fallen a distane d. Then,
or
or ( or
Integrating we get
or ………….(i)
Now magnetic force opposite to displacement x will be
A constant downward force is .

so, this is similar situation like spring clock system in vertical position. in wich a force acts upwards and a constant force acts downwards.
hence, the wire will execute SHM, where
Ampltude will be at
or
At , rod is in its extreme position.
Therefore if we write the equation from mean position we will write
But
where,
b. From Eqn i
Here
c. Maximum velocity
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Check point
Explore 60 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:SUBJECTIVE TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionCDEF is a fixed conducting smooth frame in vertical plane. A conducting uniform rod GH of mass m can move vertically and smoothly without losing contact with the frame. Gh always remains horizontal and is given velocity u upward and released. Taking the acceleration due to gravity as g and present other than R. Find out the time tasken by the rod to reach the highest point.

View Solution
Knowledge Check
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2RA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pml
A uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA conducting rod of mass 200 gm and length 10 cm can slide without friction on two long, horizontal rails. A uniform magnetic field of magnitude 5 m T exists in the region as shown. A source S is used to maintain a constant current 2 A through the rod. If motion of the rod starts from the rest, find its speed (in cm/s) after 10 s from the start of the motion
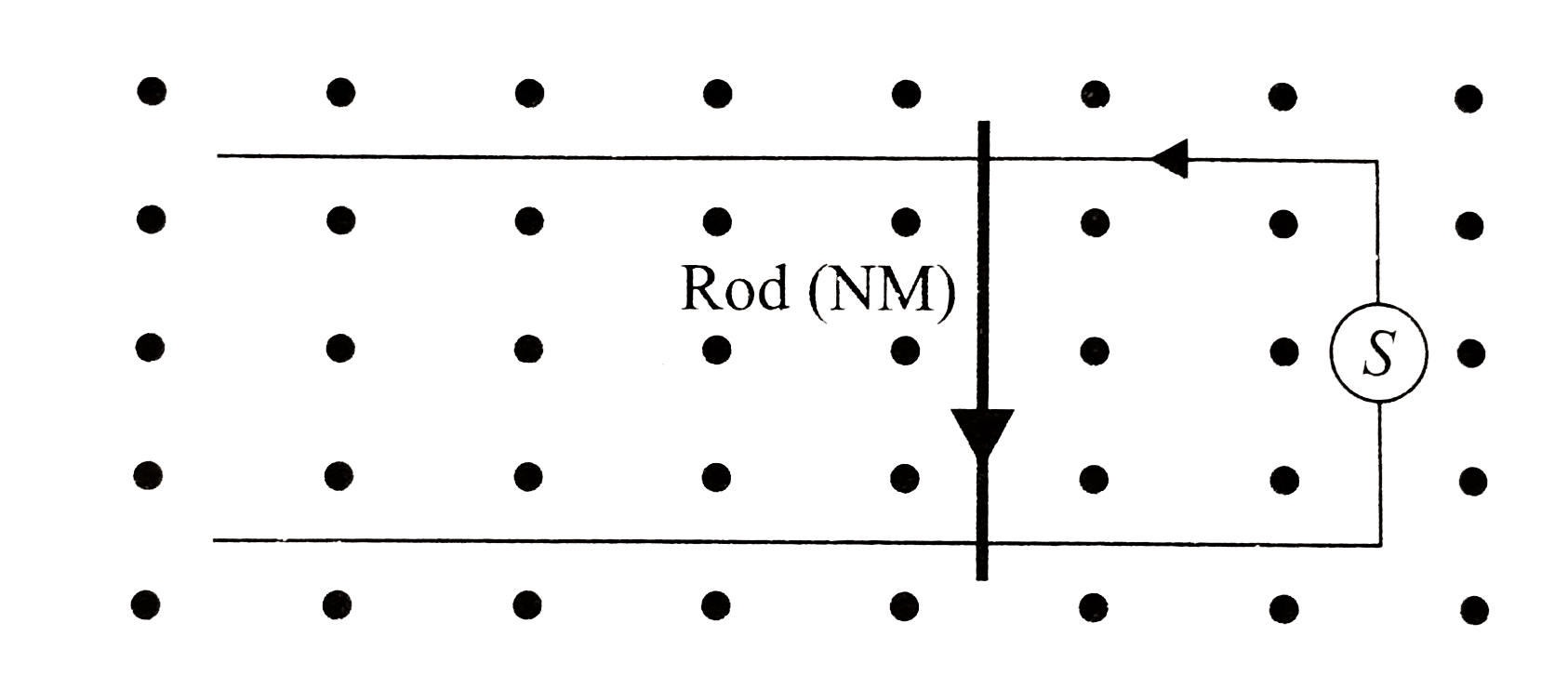
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
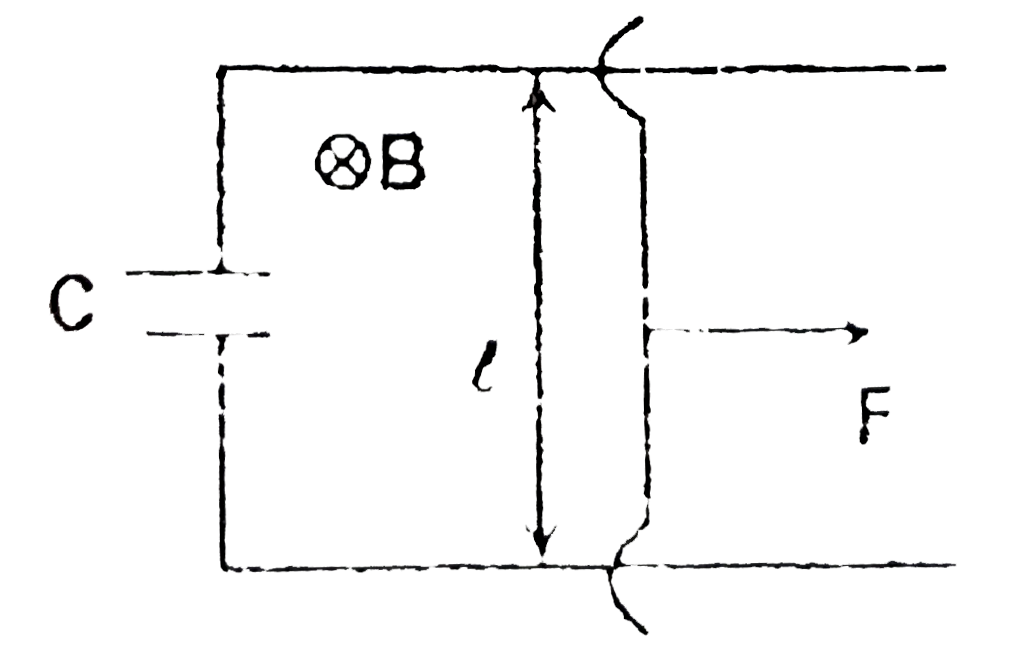
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. Whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View SolutionA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field →B exists in space. Then, magnitude of magnetic field →B is

View Solution