Charge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where
−a<x<a
x<−a
x>−a
0<x<a
The correct Answer is:B
Between 2q and −q, two electric fields are in same direction. So their resultant can't be zero. To the right of 2q left of -q they are in opposite directions. So net field will be zero nearer to charge having small magnitude.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - SUBJECTIVE_TYPE6videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Assertion And Reason19videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Charge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere
View SolutionTwo charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
View SolutionTwo identical charge of value Q each are placed at (-a,0) and (a , 0) . The end coordinates of the point where the net electric field is zero and maximum are respectively-
View SolutionTwo point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
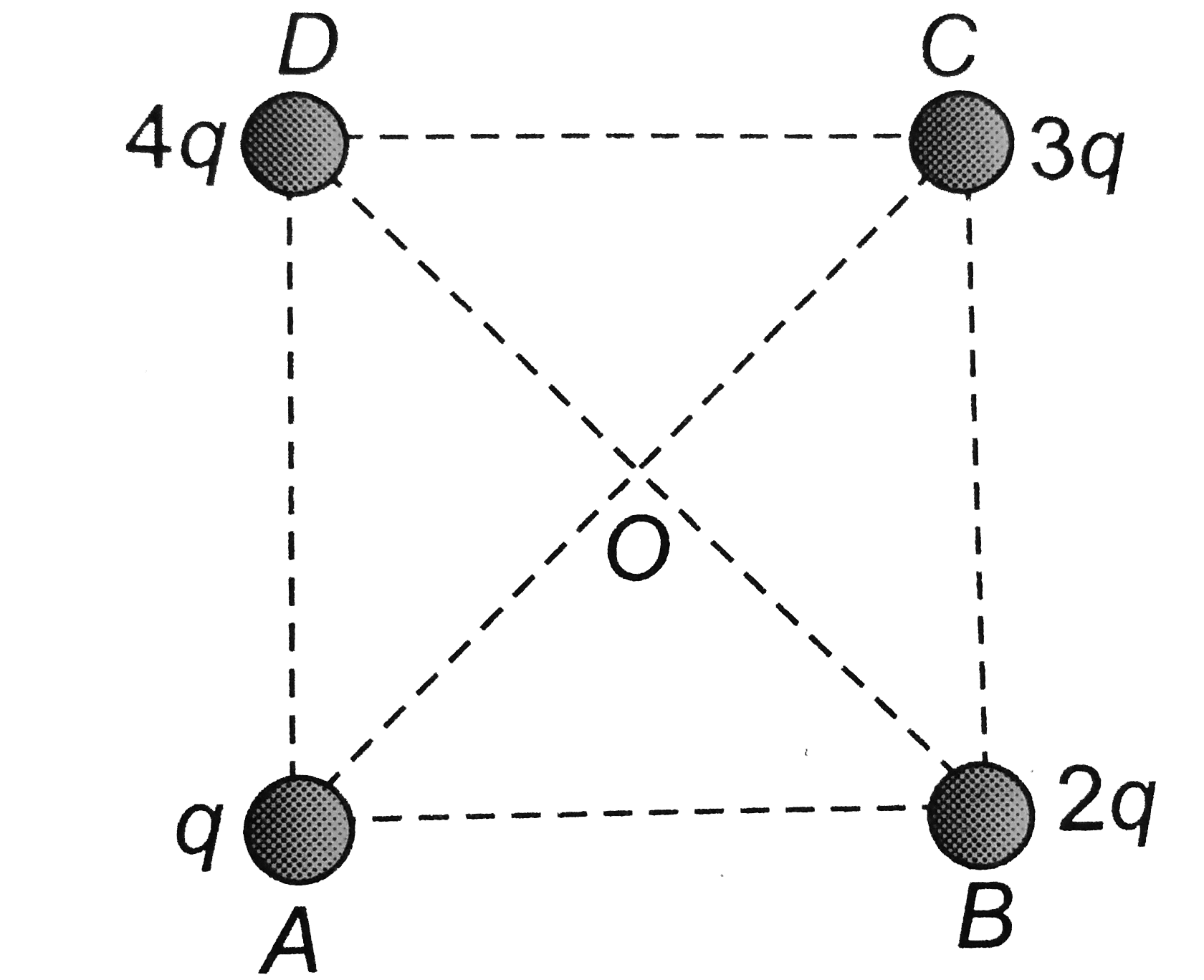View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
View SolutionFour point charges +q,+q,−qand−q are placed on the corners of a square of side length 'a' as shown in the figure. The magnitude of electric field at a point which is at a distance x(>>a) from the centre along a line perpendicular to the plane of the square and passing through the centre is
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionTwo point charges q and -2q are kept on x-axis at ( -a,0,0) and ( 2a,0,0) . Find the locus of all points wher electric potential is zero. Assume that electric potential at infinite distance from a point charge is zero.
View Solution