Eight point charges of magnitude Q are arranged to form the corners of a cube of side L. The arrangement is made in manner such that the nearest neighbour of any charge has the opposite sign. Initially, the charges are held at rest. If the system is let free to move, what happens to the arrangement? Does the cube-shape shrink or expand? Calculate the velocity ct each charge when the side-length of the cube formation changes from L to nL. Assume that the mass of each point charge is m.
To solve the problem, we need to analyze the arrangement of the charges and the potential energy associated with them. Here’s a step-by-step breakdown:
Step 1: Understanding the Configuration
We have 8 point charges of magnitude Q at the corners of a cube of side length L. The arrangement is such that each charge has a nearest neighbor with an opposite sign. This means we have alternating charges at the corners of the cube.
Step 2: Calculate the Potential Energy
The potential energy U of the system can be calculated by considering the interactions between the charges.
1. Adjacent Charges: There are 12 edges in a cube, and each edge has a pair of opposite charges. The potential energy due to adjacent charges is given by:
Uadjacent=−kQ2L×12
where k is Coulomb's constant.
2. Face Diagonal Charges: Each face of the cube has diagonals where charges of the same sign interact. The distance between these charges is L√2. There are 12 such interactions:
Uface=kQ2L√2×12
3. Body Diagonal Charges: The body diagonals connect opposite corners of the cube, with a distance of L√3. There are 4 such pairs:
Ubody=−kQ2L√3×4
4. Total Potential Energy: Combine all contributions:
Utotal=Uadjacent+Uface+Ubody
Step 3: Determine if the Cube Expands or Shrinks
To determine whether the cube expands or shrinks, we analyze the sign of the total potential energy:
- If the total potential energy is negative, the system is unstable, and the charges will repel each other, causing the cube to expand.
- If the potential energy is positive, the system is stable, and the cube will shrink.
From the calculations, we find that the negative contributions dominate, leading to the conclusion that the cube will shrink.
Step 4: Calculate the Velocity of Each Charge
When the side length of the cube changes from L to nL, we need to calculate the velocity v of each charge.
1. Change in Potential Energy: The change in potential energy will equal the gain in kinetic energy:
ΔU=Uinitial−Ufinal=gain in kinetic energy
2. Kinetic Energy of Each Charge: The kinetic energy of each charge can be expressed as:
KE=12mv2
where m is the mass of each charge.
3. Setting Up the Equation: Equating the loss in potential energy to the gain in kinetic energy:
ΔU=8×12mv2
Simplifying gives:
ΔU=4mv2
4. Solving for Velocity: Rearranging the equation to solve for v:
v=√ΔU4m
Final Expression for Velocity
Substituting the expression for ΔU derived from the potential energy calculations will yield the final expression for the velocity of each charge when the side length changes from L to nL.
We have 8 point charges of magnitude Q at the corners of a cube of side length L. The arrangement is such that each charge has a nearest neighbor with an opposite sign. This means we have alternating charges at the corners of the cube.
The potential energy U of the system can be calculated by considering the interactions between the charges.
Uadjacent=−kQ2L×12
where k is Coulomb's constant.
Uface=kQ2L√2×12
Ubody=−kQ2L√3×4
Utotal=Uadjacent+Uface+Ubody
To determine whether the cube expands or shrinks, we analyze the sign of the total potential energy:
- If the total potential energy is negative, the system is unstable, and the charges will repel each other, causing the cube to expand.
- If the potential energy is positive, the system is stable, and the cube will shrink.
When the side length of the cube changes from L to nL, we need to calculate the velocity v of each charge.
ΔU=Uinitial−Ufinal=gain in kinetic energy
KE=12mv2
where m is the mass of each charge.
ΔU=8×12mv2
Simplifying gives:
ΔU=4mv2
v=√ΔU4m
Substituting the expression for ΔU derived from the potential energy calculations will yield the final expression for the velocity of each charge when the side length changes from L to nL.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.110videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.215videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective15videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionFour charges +q,−q,+q and −q are placed in order on the four consecutive corners of a square of side a. The work done in interchanging the positions of any two neighboring charges of the opposite sign is
View Solution
Knowledge Check
- Question 1 - Select One
Four charges are arranged at the corners of a square ABCD, as shown in the adjoining figure. The force on the charge kept at the centre O is
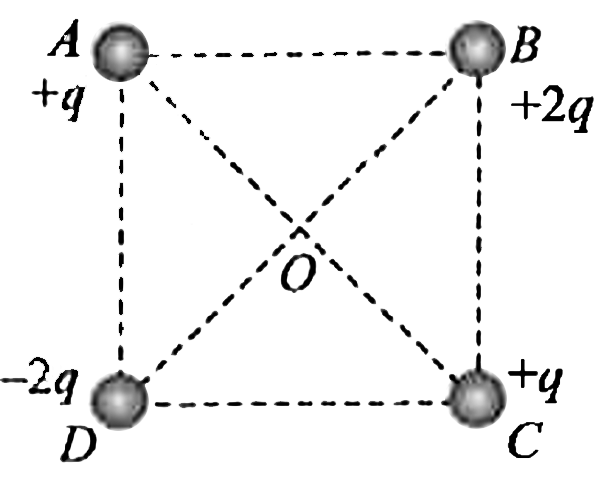 Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Aalong the diagonal BDBalong the diagonal ACCzeroDperpendicular to side AB
Eight equal point charges are placed at corners of a cube side length a. The potential and electric field magnitude at the centre of cube will be
View SolutionCharges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
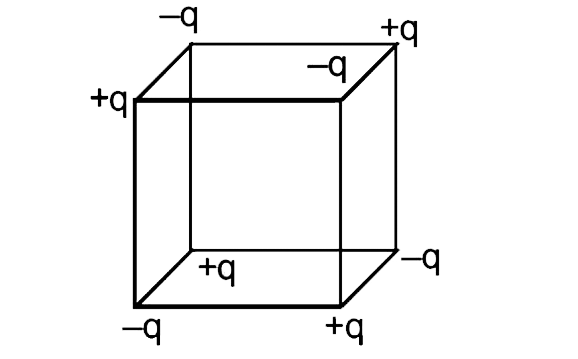 View Solution
View SolutionA charge +q is placed at the mid point of a cube of side L. The electric flux emerging from cube is
View SolutionA charge Q is placed at the corner of a cube of edge length L. The electric flux linked to one of the faces not touching the charge Q is
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
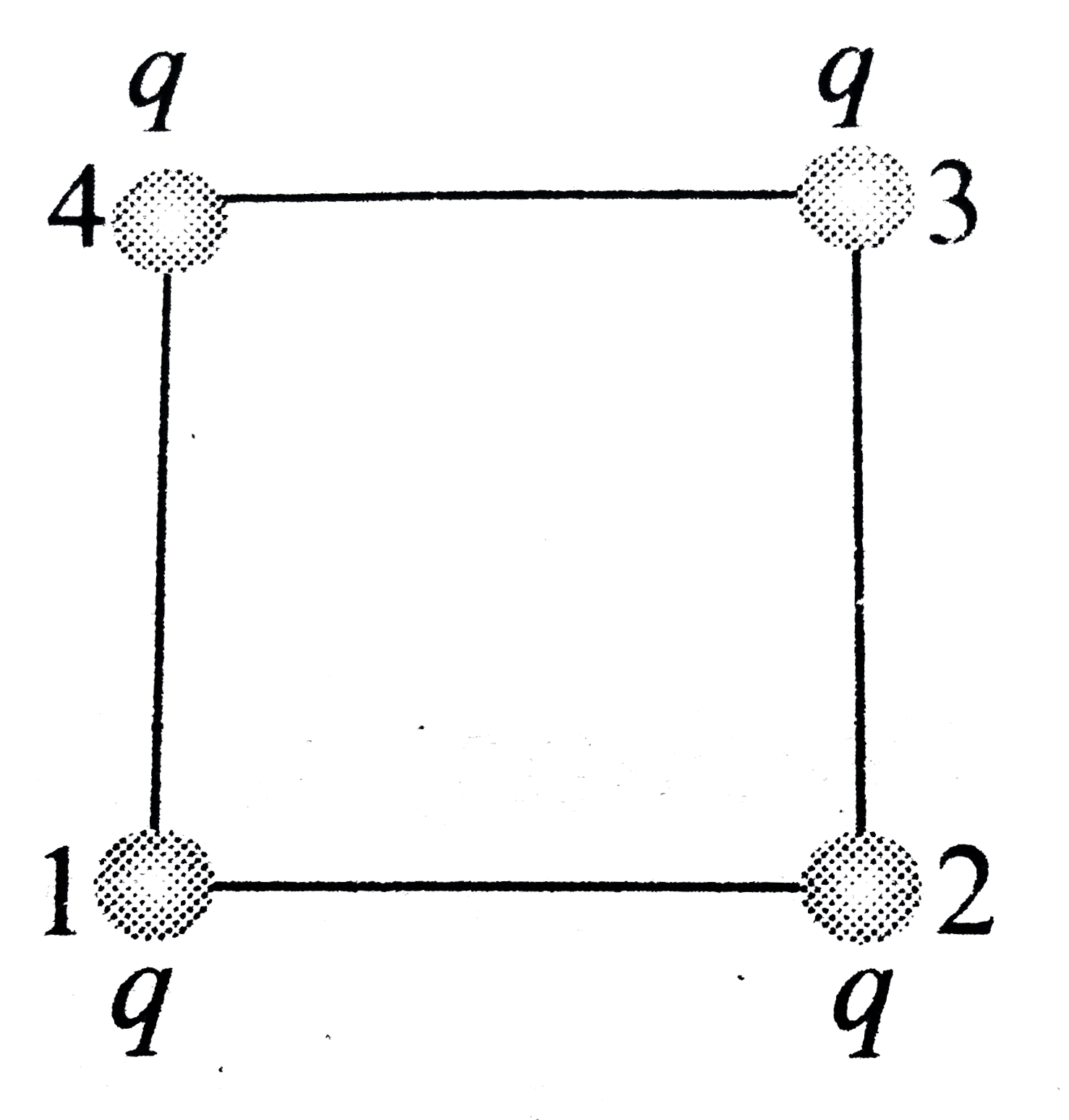 .View Solution
.View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionFour charges are arranged at the corners of a square ABCD as shown in the figure. The force on the charge kept at the centre O will be:
 View Solution
View Solution

