Consider a frictionless ramp on which a smooth object is made to slide down from an initial height 'h'. The distance 'd' necessary to stop the object on a flat track of coefficient of friction 'μ.'), kept at the ramp end is
h/μ
μh
μ2h
h2μ
The correct Answer is:A
To solve the problem, we need to determine the distance 'd' that an object will slide on a flat track with a coefficient of friction 'μ' after sliding down a frictionless ramp from an initial height 'h'.
1. Identify the Initial Energy:
When the object is at height 'h', it has gravitational potential energy given by:
PE=mgh
where m is the mass of the object and g is the acceleration due to gravity.
2. Energy Conversion:
As the object slides down the ramp, this potential energy is converted into kinetic energy (KE) at the bottom of the ramp. The kinetic energy at the bottom is given by:
KE=12mv2
At the bottom of the ramp, all potential energy has been converted into kinetic energy:
mgh=12mv2
3. Solve for Velocity:
We can cancel m from both sides (assuming m≠0):
gh=12v2⟹v2=2gh⟹v=√2gh
4. Determine the Work Done by Friction:
When the object reaches the flat surface, it will experience a frictional force that does work against its motion. The frictional force Ff is given by:
Ff=μmg
The work done by friction Wf over the distance 'd' is:
Wf=−Ff⋅d=−μmgd
(The negative sign indicates that the work done by friction is in the opposite direction of the motion.)
5. Apply the Work-Energy Principle:
According to the work-energy theorem, the work done by friction will equal the change in kinetic energy:
Wf=ΔKE
Since the object comes to a stop, the final kinetic energy is zero, and the initial kinetic energy is 12mv2:
−μmgd=0−12mv2
Substituting v2=2gh:
−μmgd=−12m(2gh)
6. Simplify the Equation:
Cancel m from both sides (assuming m≠0):
μgd=gh
Rearranging gives:
d=ghμg=hμ
Final Answer:
Thus, the distance 'd' necessary to stop the object on the flat track is:
d=hμ
When the object is at height 'h', it has gravitational potential energy given by:
PE=mgh
where m is the mass of the object and g is the acceleration due to gravity.
As the object slides down the ramp, this potential energy is converted into kinetic energy (KE) at the bottom of the ramp. The kinetic energy at the bottom is given by:
KE=12mv2
At the bottom of the ramp, all potential energy has been converted into kinetic energy:
mgh=12mv2
We can cancel m from both sides (assuming m≠0):
gh=12v2⟹v2=2gh⟹v=√2gh
When the object reaches the flat surface, it will experience a frictional force that does work against its motion. The frictional force Ff is given by:
Ff=μmg
The work done by friction Wf over the distance 'd' is:
Wf=−Ff⋅d=−μmgd
(The negative sign indicates that the work done by friction is in the opposite direction of the motion.)
According to the work-energy theorem, the work done by friction will equal the change in kinetic energy:
Wf=ΔKE
Since the object comes to a stop, the final kinetic energy is zero, and the initial kinetic energy is 12mv2:
−μmgd=0−12mv2
Substituting v2=2gh:
−μmgd=−12m(2gh)
Cancel m from both sides (assuming m≠0):
μgd=gh
Rearranging gives:
d=ghμg=hμ
Thus, the distance 'd' necessary to stop the object on the flat track is:
d=hμ
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
157 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
An object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
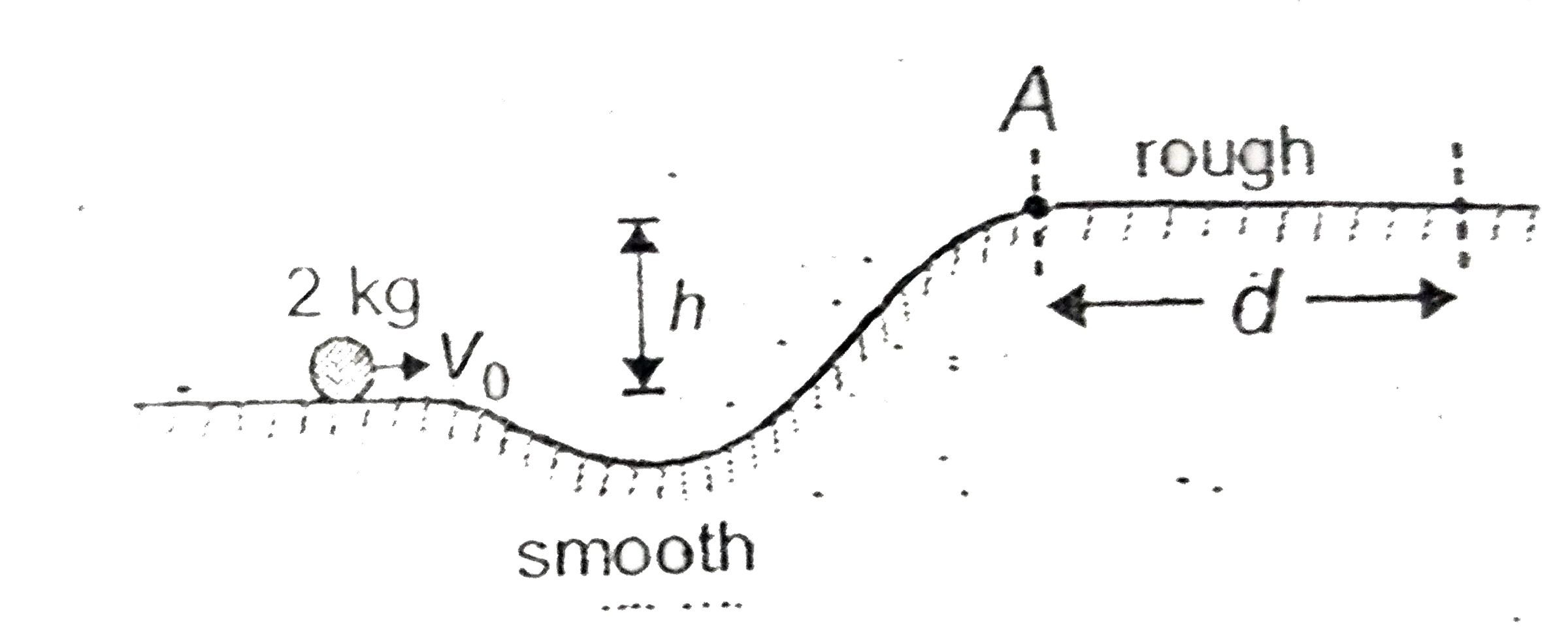
The speed of body at the higher level A is
View SolutionA brick is projected from ground with speed v at angle θ from horizontal. The longer face of brick is parallel to ground. The brick slides along ground through some distance after hitting ground and then stops. The collision is perfectly inelastic. The coefficient of friction is μ(μ<cotθ). The angle θ is chosen such that brick travels the maximum horizontal distance before coming to rest. Find the distance in meters :
View SolutionIn the arrangement shown in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2. What is the maximum distance d travelled by body on rough surface?
View SolutionA rocket is fired vertically from the earth with an acceleration of 2g, where g is the gravitational acceleration. On an inclined plane inside the tocket, making an angle θ with the horizontal, a point object of mass m is kept, the minimum coefficient of friction μmin between the mass and the inclined suface such that the mass does not move is:
View SolutionA given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
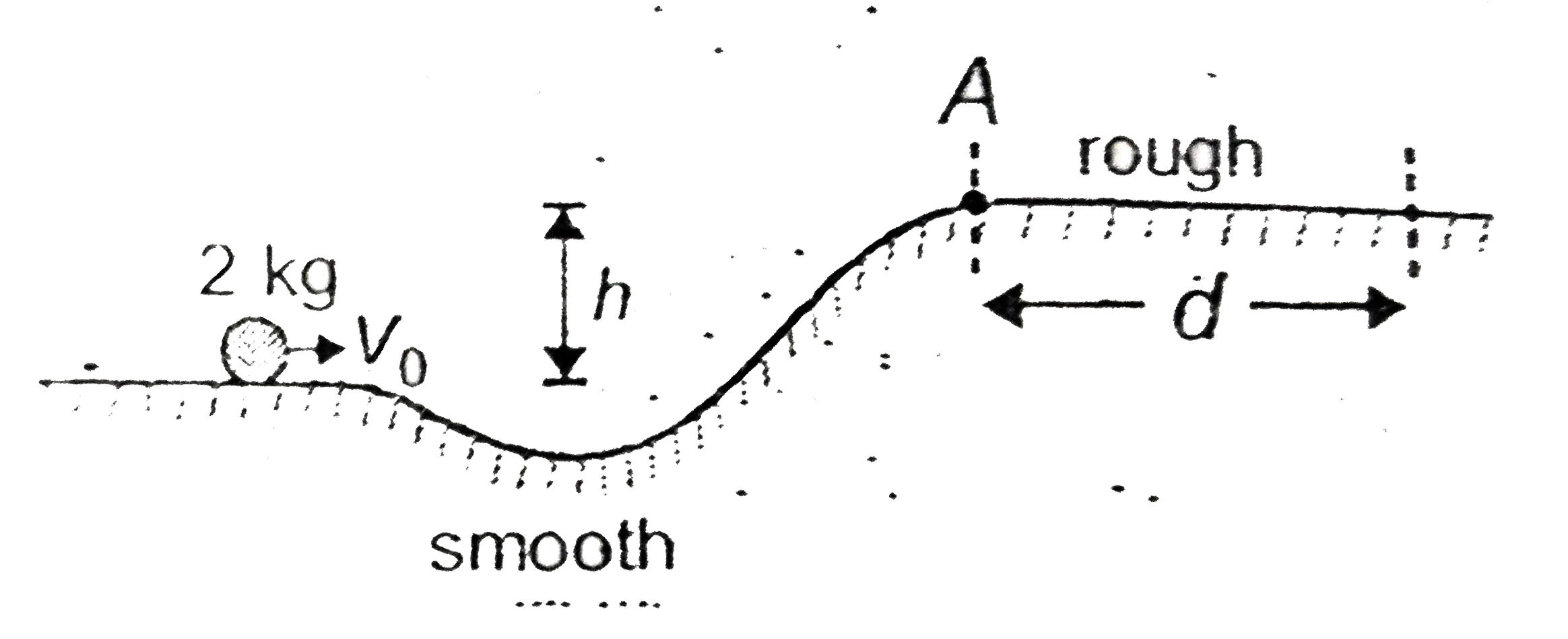
What is the work done by friction force on the body during the motion.
View Solution
