Consider a pulley fixed at its centre of mass by a clamp. A light rope is wound over it and the free end is tied to block. The tension in the rope is T. a. Write the forces acting on the pulley. How are they related? B. Locate the axis of rotation. c. Find the torque of the forces abut the axis of rotation.
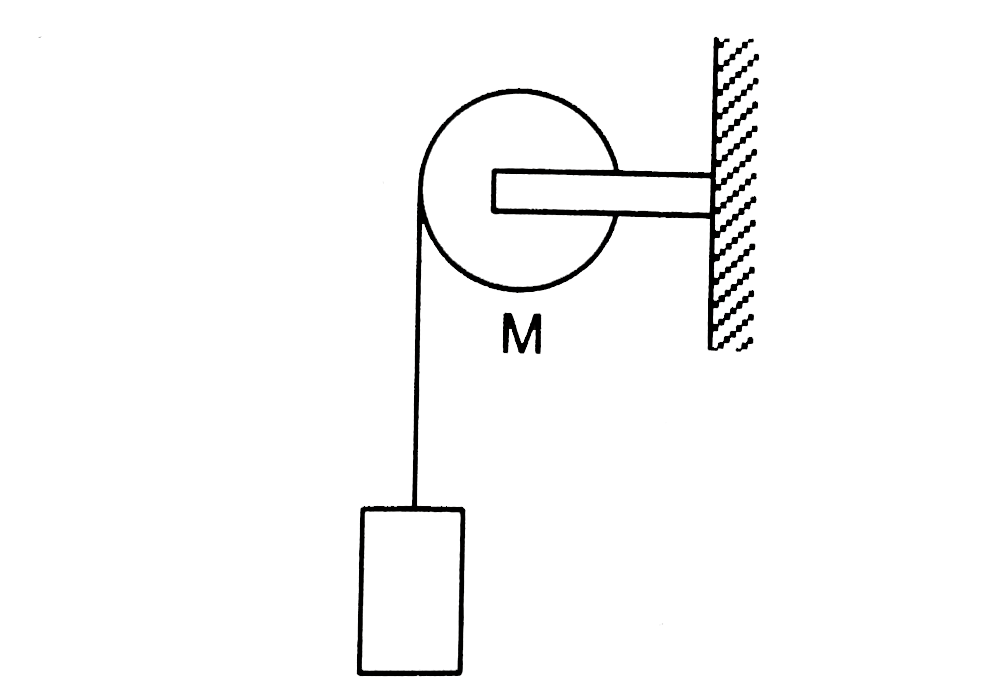
a. the forces on the pulley are ure.
i. attraction by the earth Mg vertically downward
ii tension tl by the rope along the rope
iii contact force N by the support at the centre.
N=T+Mg (centre of mass of the pulley is at rest so Newoton's 1st law applies.
b. The axis of rotation is the line through the centre of the pulley and perpendicular to theplane of the pulley.
c. Let us take the positive direction of the axis towards the reader.
The force Mg passses through the centre of mass and it intersects the axis of rotation. Hence the torque of Mg abut teh axils is zero (casse II). Similarly the torque of the contct force N is also zero.
The tension T is along the tangent of the rim in the vertically downward direction. The tension and the axis of rotation are perpendicular but never intersect. Case III applies. Join the point where the rope leaves the rim to the centre. TGhis line is the common perpendicular tot the tension and the axis. Hence the torque is T.r (positive, since it wil try to rotate the ulley anticlockwise).
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples29videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -126videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A 2.00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
View SolutionA block A of mass 8 kg is placed on a frictionless horizontal table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 2 kg at the other end. Find the acceleration of the system. Also find the tension in the thread. If the thread is cut into two and tied to the ends of a spring of forceconstant 1600N/m, find the amount of stretching of the spring. Neglect the mass of thread and of spring (g=9.8m/s2)
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View SolutionA particle of mass m is tied to light string and rotated with a speed v along a circular path of radius r. If T=tension in the string and mg= gravitational force on the particle then actual forces acting on the particle are
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
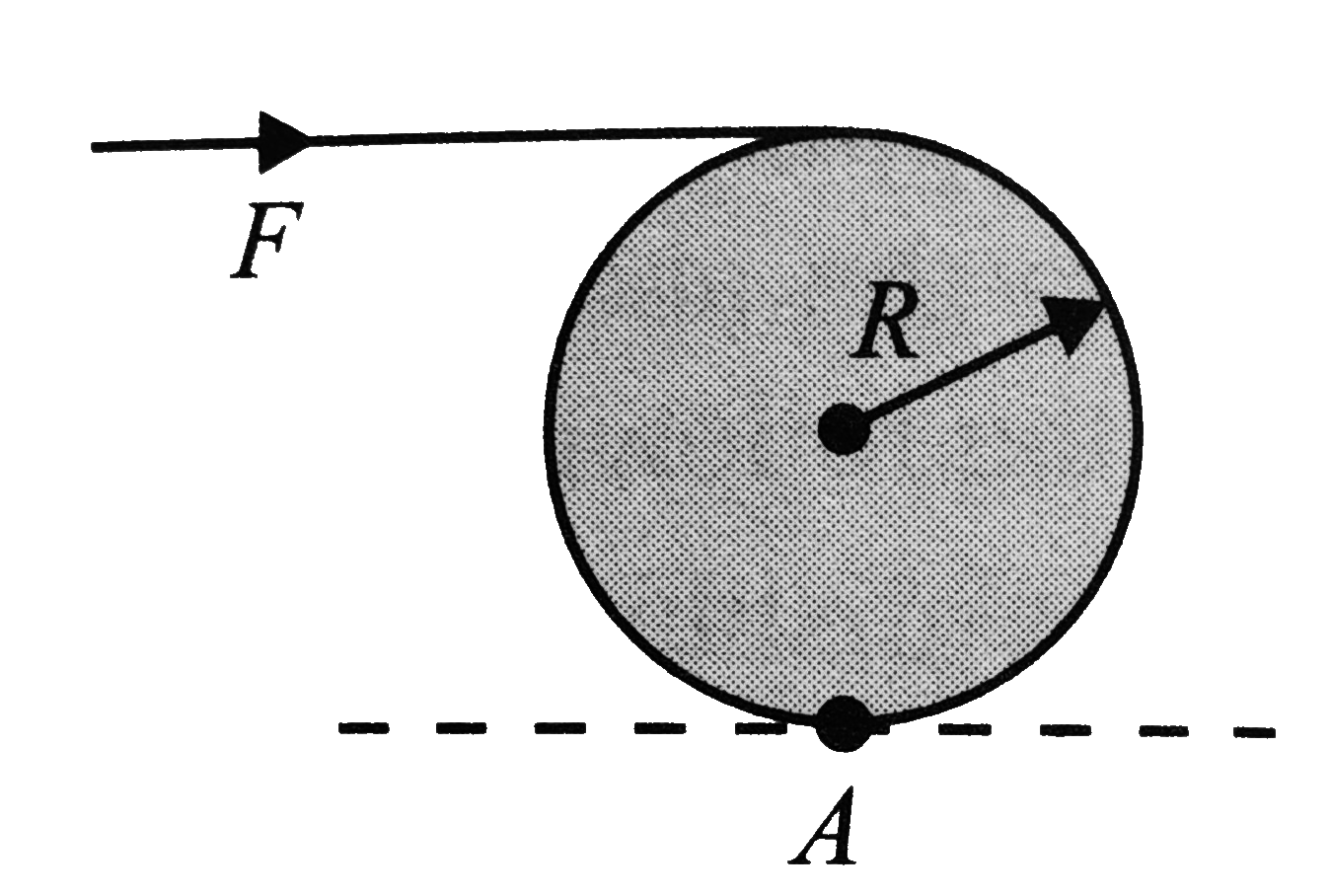
Tangential acceleration of the centre of mass isView SolutionA short dipole is placed along the x - axis at x=x (Fig. 3.120).
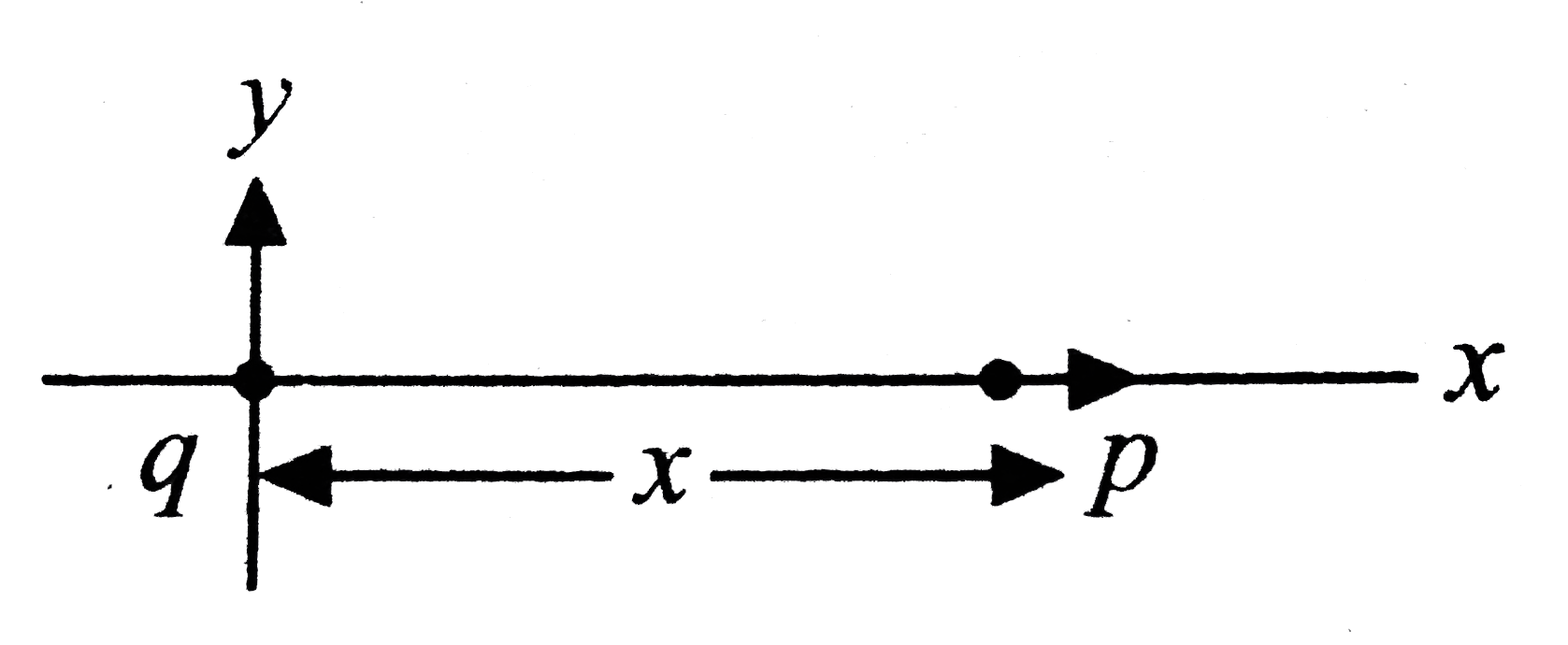 .
.
a. Find the force acting on the dipole due to a point charge q placed at the origin.
b. Find the force on the dipole if the dipole is rotated by 180∘ about the z- axis.
c. Find the force on dipole if the dipole is rotated by 90∘ anticlockwise about z - axis, i.e., it becomes parallel to the y - axis.View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
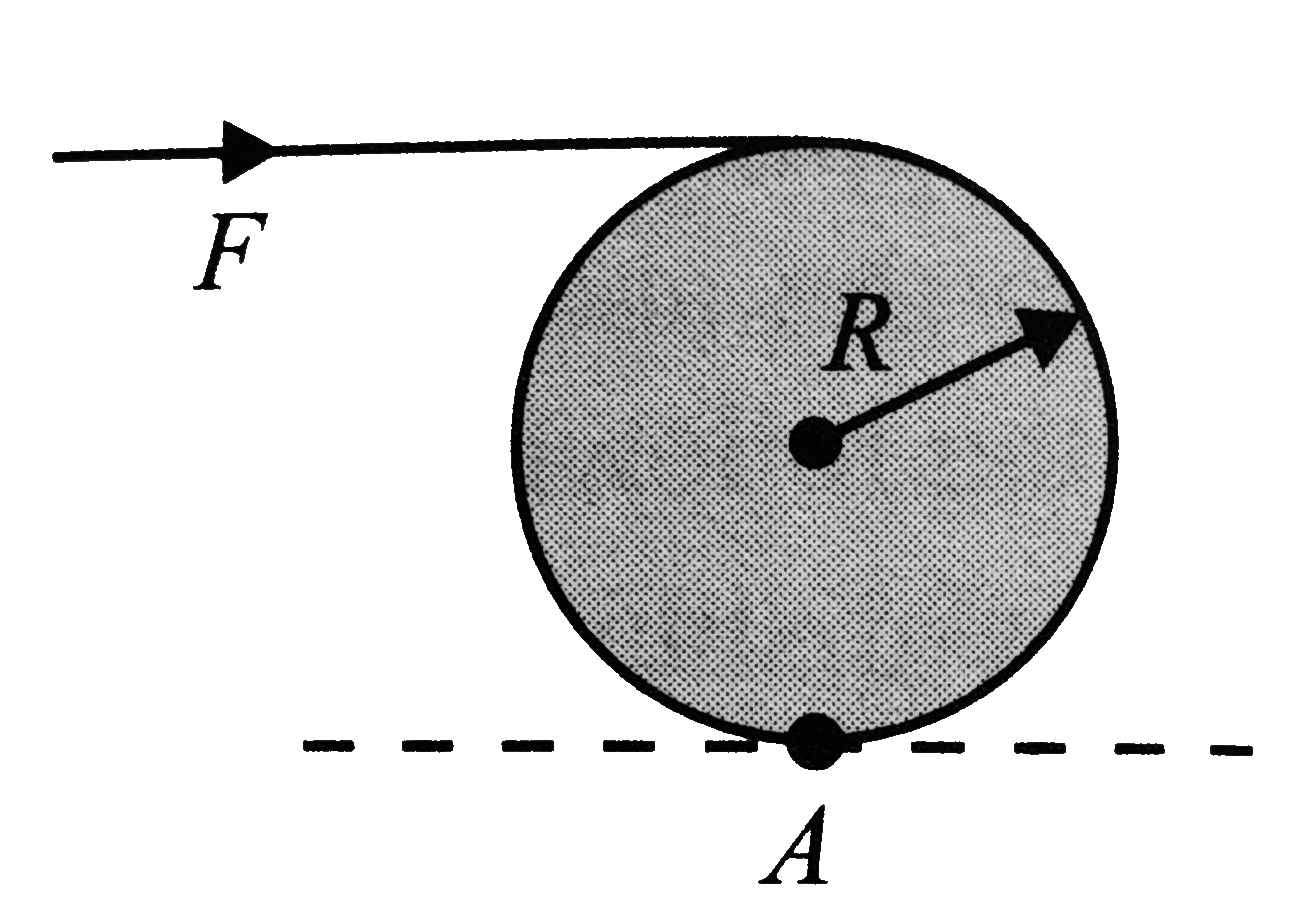
Component of reaction at the hinge in the horizontal direction isView SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
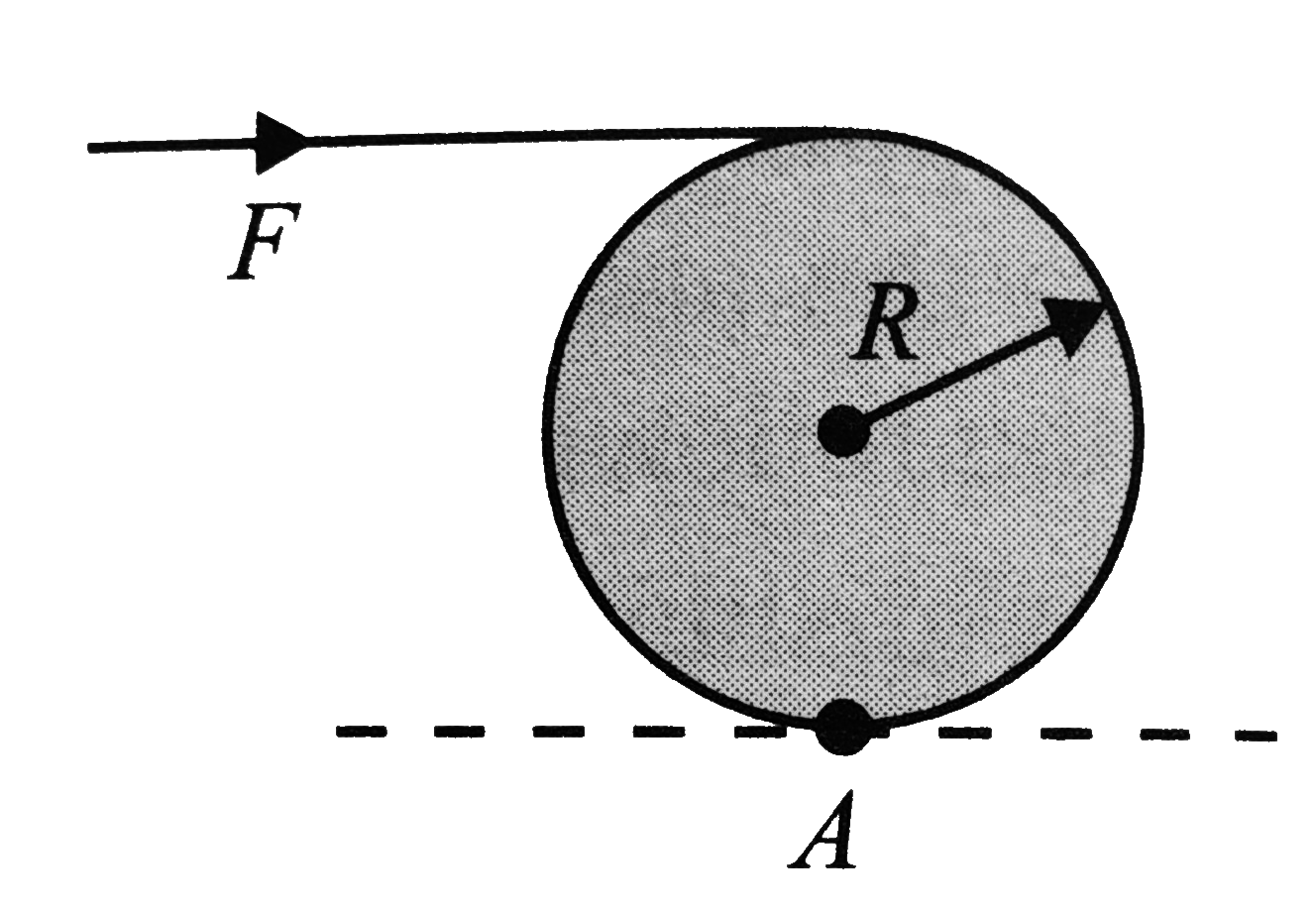
Component of reaction at the hinge in the vertical direction isView Solution

