Consider Example 22. Takin the coefficient of friction, μ to be 0.5, calculate the maximum compression of the spring.
To solve the problem of calculating the maximum compression of the spring when the coefficient of friction, μ, is 0.5, we will follow these steps:
Step 1: Identify the Forces Acting on the Object
We need to consider the forces acting on the object that compresses the spring. The forces include:
- The gravitational force acting downward, Fg=mg.
- The spring force acting upward when compressed, Fs=kx.
- The frictional force acting opposite to the direction of motion, Ff=μmg.
Step 2: Write the Work Done by the Forces
The work done by the frictional force is given by:
Wf=−μmgx
The work done by the spring force is:
Ws=−12kx2
Step 3: Apply the Work-Energy Theorem
According to the work-energy theorem, the total work done on the object is equal to the change in kinetic energy:
Wtotal=ΔKE
Since we assume the object starts from rest, the initial kinetic energy is zero, and thus:
Wf+Ws=12mv2
Substituting the expressions for work done:
−μmgx−12kx2=0−12mv2
Step 4: Rearrange the Equation
Rearranging gives us:
12kx2+μmgx−12mv2=0
This is a quadratic equation in the form of:
Ax2+Bx+C=0
where:
- A=12k
- B=μmg
- C=−12mv2
Step 5: Apply the Quadratic Formula
Using the quadratic formula x=−B±√B2−4AC2A:
x=−μmg±√(μmg)2+2k⋅12mv2k
Step 6: Substitute Known Values
Substituting μ=0.5 into the equation, we can find the maximum compression x. Assuming we know the values of m, g, and k, we can compute x.
Step 7: Calculate the Maximum Compression
After substituting the values, we find that:
x≈1.35 m
Final Answer
The maximum compression of the spring is x=1.35 m.
---
We need to consider the forces acting on the object that compresses the spring. The forces include:
- The gravitational force acting downward, Fg=mg.
- The spring force acting upward when compressed, Fs=kx.
- The frictional force acting opposite to the direction of motion, Ff=μmg.
The work done by the frictional force is given by:
Wf=−μmgx
The work done by the spring force is:
Ws=−12kx2
According to the work-energy theorem, the total work done on the object is equal to the change in kinetic energy:
Wtotal=ΔKE
Since we assume the object starts from rest, the initial kinetic energy is zero, and thus:
Wf+Ws=12mv2
Substituting the expressions for work done:
−μmgx−12kx2=0−12mv2
Rearranging gives us:
12kx2+μmgx−12mv2=0
This is a quadratic equation in the form of:
Ax2+Bx+C=0
where:
- A=12k
- B=μmg
- C=−12mv2
Using the quadratic formula x=−B±√B2−4AC2A:
x=−μmg±√(μmg)2+2k⋅12mv2k
Substituting μ=0.5 into the equation, we can find the maximum compression x. Assuming we know the values of m, g, and k, we can compute x.
After substituting the values, we find that:
x≈1.35 m
The maximum compression of the spring is x=1.35 m.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Knowledge Check
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
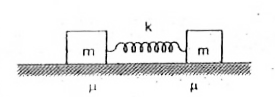 A2μmg/kBμmg/kCzeroDnot possible
A2μmg/kBμmg/kCzeroDnot possible
Assuming the length of a chain to be L and coefficient of static friction μ. Compute the maximum length of the chain which can be held outside a table without sliding.
View SolutionWhen the coefficient of friction between the weight and the palte is μ.
View SolutionQuestions |Maximum Compression Of A Spring|Questions
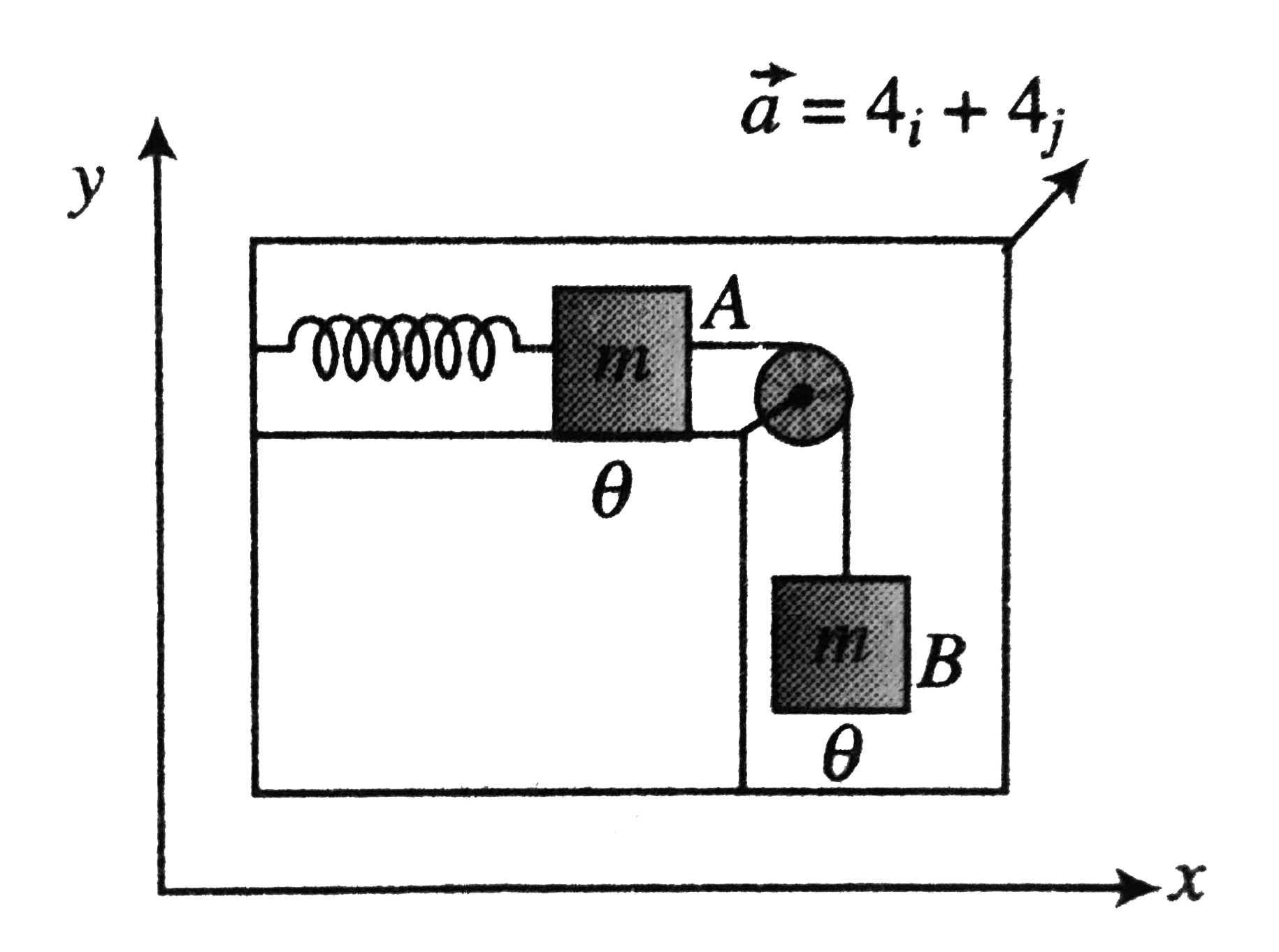
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).
View SolutionThe coefficient of friction between two surface is 0.2. The maximum angle of friction is
View Solution