In each ring all points are at same potential

Consider the circuit shown below. When switch $S_{1}$ is closed, let I be the current at time t, then applying Kirchhoff's law
$E - i R - L \frac{d i}{d t} = 0 or \int_{0}^{i} \frac{d i}{E - i R} = \frac{1}{L} \int_{0}^{1} d t$
$i = \frac{E}{R} (1 - e^{- \frac{R}{l} \cdot t})$
$\frac{L}{R}$ = time constant of circuit
When current reaches its steady value $(= i_{0}$ , open $S_{1}$ and close $S_{2}$ , the current does reach to zero finally but decays expnentially. The decay equation is given as $i = i_{0} e^{- \frac{R}{L} \cdot T}$ .
ocr_image
A wire is sliding as shown in fig . The angle between the acceleration and velocity of the wire is

View Solution

Consider the circuit shown below. When switch $S_{1}$ is closed, let I be the current at time t, then applying Kirchhoff's law
$E - i R - L \frac{d i}{d t} = 0 or \int_{0}^{i} \frac{d i}{E - i R} = \frac{1}{L} \int_{0}^{1} d t$
$i = \frac{E}{R} (1 - e^{- \frac{R}{l} \cdot t})$
$\frac{L}{R}$ = time constant of circuit
When current reaches its steady value $(= i_{0}$ , open $S_{1}$ and close $S_{2}$ , the current does reach to zero finally but decays expnentially. The decay equation is given as $i = i_{0} e^{- \frac{R}{L} \cdot T}$ ).
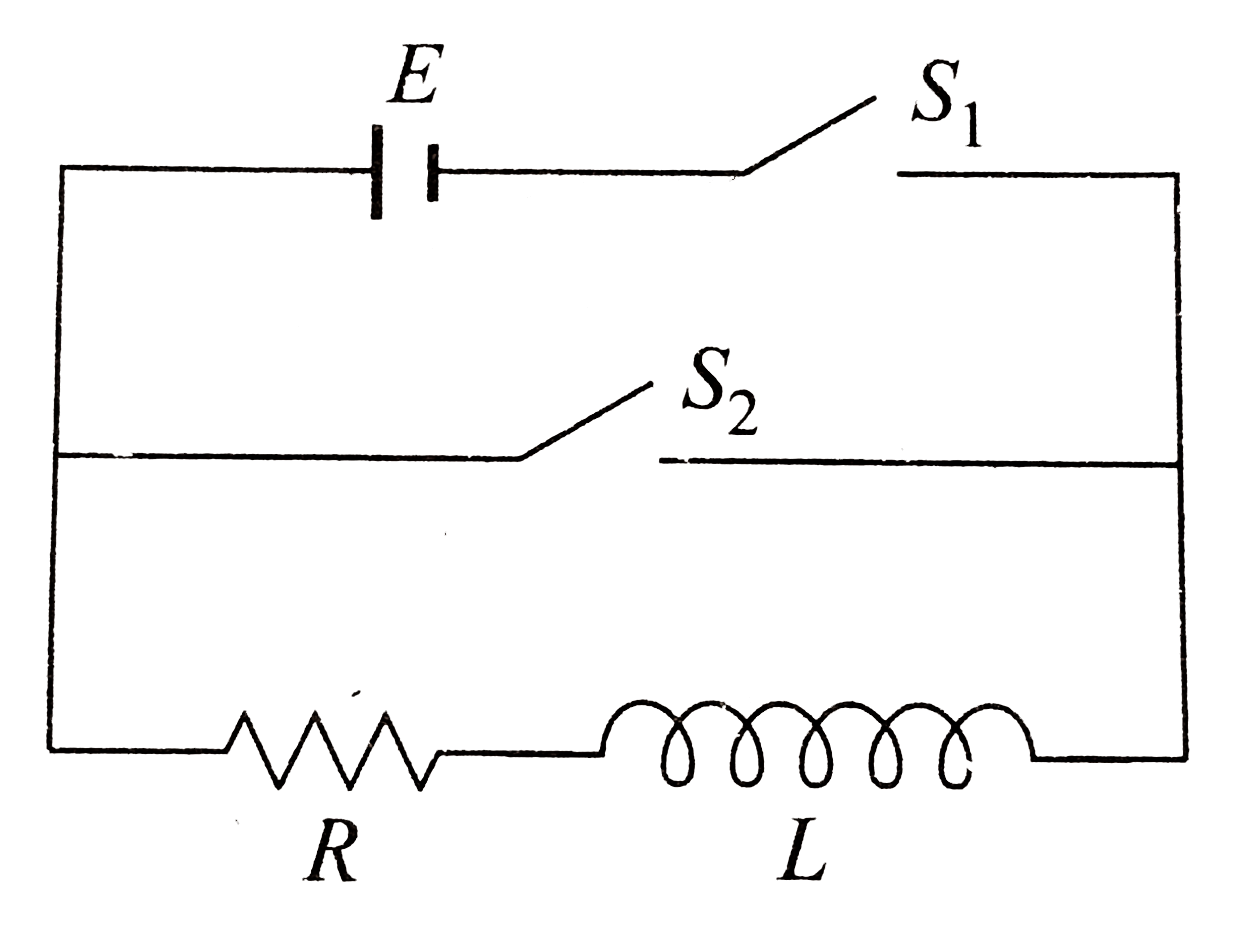
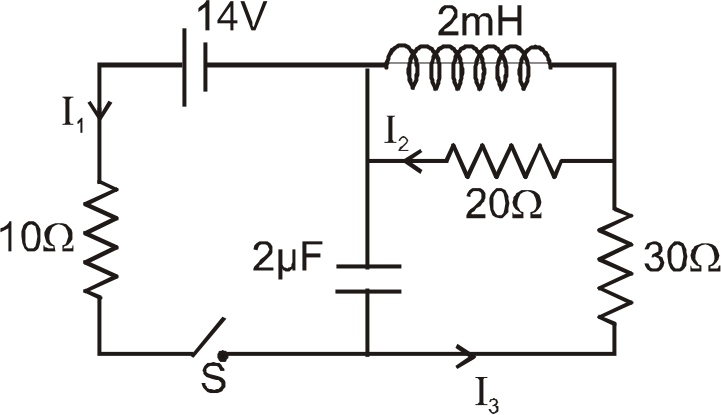
ocr_image
When a coil carrying a steady current is short circuited, the current decreases in it $η$ times in time $t_{0}$ . The time constant of the circuit is

View Solution

In the circuit shown, the switch is closed at $t = 0$ , the currents $I_{1}, I_{2}$ and $I_{3}$ are
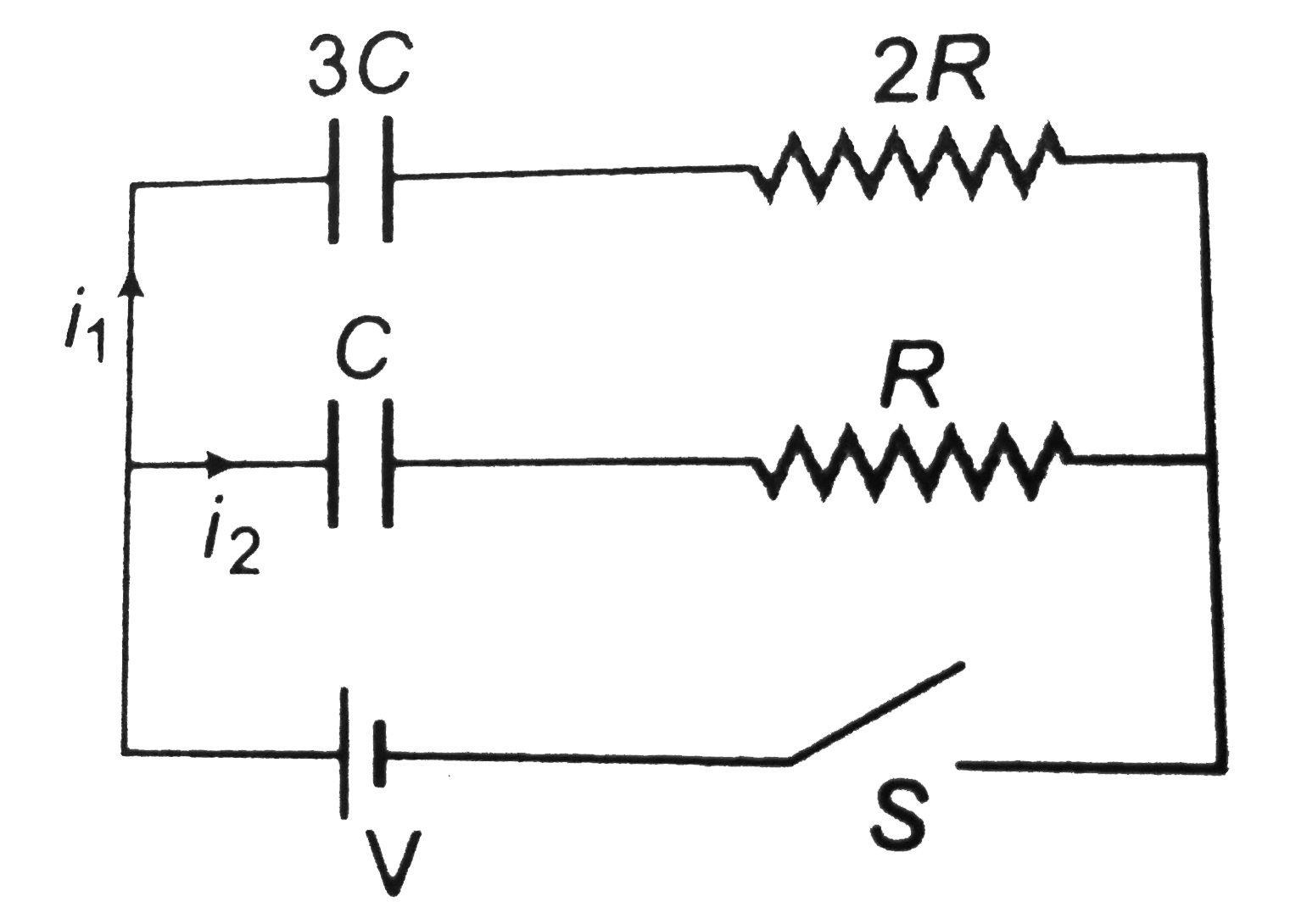
ocr_image

View Solution

In the circuit shown switch $S$ is closed at $t = 0$ . Let $i_{1}$ and $i_{2}$ be the current at any finite time t then the ratio $\frac{i_{1}}{i_{2}}$
ocr_image

View Solution

In the circuit shown in figure switch S is closed at time t=0
ocr_image
Current I from the battery at time t is given by

View Solution

In the circuit shown, the switch 'S' is closed at $t = 0$ . Then the current through the battery steady state reached is
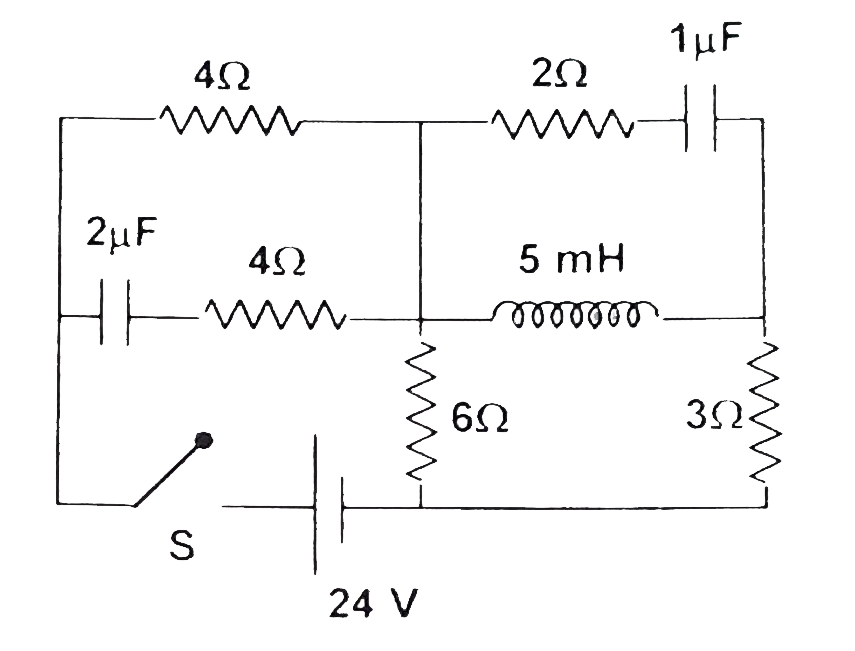ocr_image

View Solution

Switch is closed at $t = 0$ then the current in the circuit at $t = \frac{L}{2} R$ is ocr_image

View Solution

In the circuit shwon in fig. switch S is closed at time t = 0. Let $I_{1} and I_{2}$ be the currents at any finite time t, then the ratio $I_{1} / I_{2}$
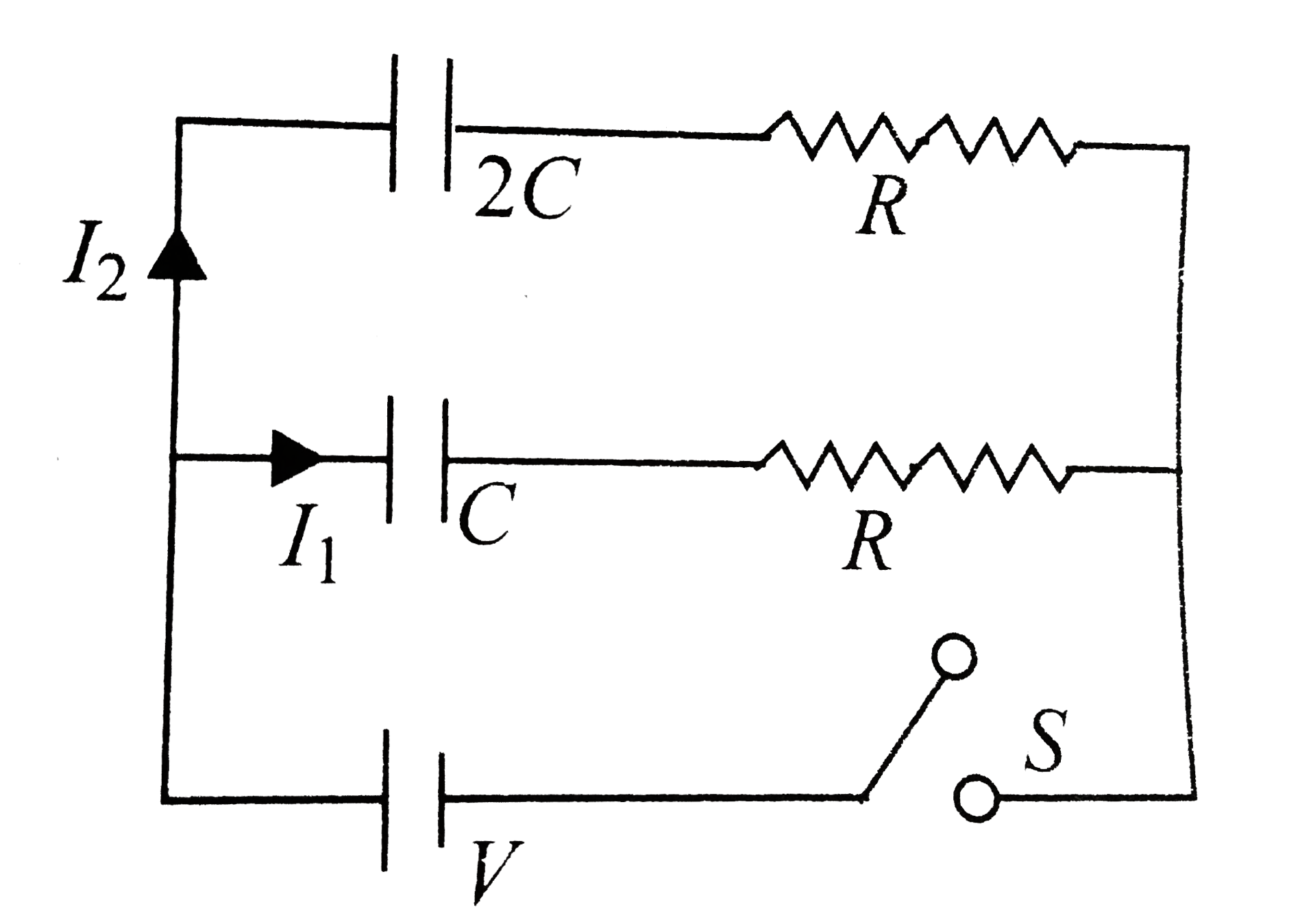ocr_image

View Solution

In the circuit shown, switch $S$ is closed at time $t = 0$ . Find the current through the inductor as a function of time $t$ .
ocr_image

View Solution

In the circuit shown in figure $L = 10 H, R = 5 Ω, E = 15 V .$ The switch $S$ is closed at $t = 0$ . At $t = 2 s$ the current in the circuit is
ocr_image

View Solution

The correct Answer is:A

Current in L-R circuit is given as $i = i_{0} (1 - e^{- t / τ})$
where $i_{0} = \frac{E}{R} and τ = \frac{L}{R}$
$Q = \int_{0}^{τ} (1 - e^{- t / τ}) d t = i_{0} {[t - \frac{e^{- t / τ}}{- 1 / τ}]}_{0}^{τ} = \frac{i_{0} τ}{e}$
$Q = i_{0} τ / e$ .

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-MISCELLANEOUS VOLUME 5-Linked Comprehension

The correct Answer is:A

Current in L-R circuit is given as i=i0(1−e−t/τ) where i0=ERandτ=LR Q=∫τ0(1−e−t/τ)dt=i0[t−e−t/τ−1/τ]τ0=i0τe Q=i0τ/e.

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-MISCELLANEOUS VOLUME 5-Linked Comprehension

Current in L-R circuit is given as $i = i_{0} (1 - e^{- t / τ})$
where $i_{0} = \frac{E}{R} and τ = \frac{L}{R}$
$Q = \int_{0}^{τ} (1 - e^{- t / τ}) d t = i_{0} {[t - \frac{e^{- t / τ}}{- 1 / τ}]}_{0}^{τ} = \frac{i_{0} τ}{e}$
$Q = i_{0} τ / e$ .