Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed (ω) as shown in the figure. Find the current in the rod when −AOC=90∘
53Ba2ωR
83Ba2ωR
Ba2ω3R
None of these
The correct Answer is:B
To solve the problem, we need to find the current in the rod when the angle AOC is 90 degrees. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a circular loop with a resistance R uniformly distributed along its length. The rod OA is rotating with a uniform angular speed ω. When ∠AOC=90∘, the rod is perpendicular to the radius at point A.
Step 2: Determine the Length of the Rod
When ∠AOC=90∘, the length of the rod OA can be denoted as L. The length of the circular arc AB can be expressed as:
LAB=14×2πr=πr2
where r is the radius of the circular loop.
Step 3: Calculate the Resistance of the Arc
The total resistance R is uniformly distributed along the circular loop. The resistance of the arc AB can be calculated as:
RAB=RTotal Length×Length of Arc AB=R2πr×πr2=R4
The remaining arc AOB has a length of 3πr2, so its resistance is:
RAOB=R2πr×3πr2=3R4
Step 4: Find the Equivalent Resistance
Since the resistances RAB and RAOB are in parallel, we can find the equivalent resistance Req using the formula for resistors in parallel:
1Req=1RAB+1RAOB=1R4+13R4=4R+43R=12+43R=163R
Thus, the equivalent resistance is:
Req=3R16
Step 5: Calculate the Induced EMF
The induced EMF E in the rod can be calculated using the formula:
E=B⋅L⋅v
where v is the linear velocity of the end of the rod, given by v=a2ω. Therefore, the EMF becomes:
E=B⋅L⋅(a2ω)=B⋅a⋅(a2ω)=12Ba2ω
Step 6: Calculate the Current
Using Ohm's law, the current I in the circuit can be calculated as:
I=EReq=12Ba2ω3R16=83Ba2ωR
Final Answer
Thus, the current in the rod when ∠AOC=90∘ is:
I=83Ba2ωR
We have a circular loop with a resistance R uniformly distributed along its length. The rod OA is rotating with a uniform angular speed ω. When ∠AOC=90∘, the rod is perpendicular to the radius at point A.
When ∠AOC=90∘, the length of the rod OA can be denoted as L. The length of the circular arc AB can be expressed as:
LAB=14×2πr=πr2
where r is the radius of the circular loop.
The total resistance R is uniformly distributed along the circular loop. The resistance of the arc AB can be calculated as:
RAB=RTotal Length×Length of Arc AB=R2πr×πr2=R4
The remaining arc AOB has a length of 3πr2, so its resistance is:
RAOB=R2πr×3πr2=3R4
Since the resistances RAB and RAOB are in parallel, we can find the equivalent resistance Req using the formula for resistors in parallel:
1Req=1RAB+1RAOB=1R4+13R4=4R+43R=12+43R=163R
Thus, the equivalent resistance is:
Req=3R16
The induced EMF E in the rod can be calculated using the formula:
E=B⋅L⋅v
where v is the linear velocity of the end of the rod, given by v=a2ω. Therefore, the EMF becomes:
E=B⋅L⋅(a2ω)=B⋅a⋅(a2ω)=12Ba2ω
Using Ohm's law, the current I in the circuit can be calculated as:
I=EReq=12Ba2ω3R16=83Ba2ωR
Thus, the current in the rod when ∠AOC=90∘ is:
I=83Ba2ωR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Consider the situation shown in the figure of the previous problem. Suppose the wire connecting O and C has zero resistance but circular loop has a resistance R uniformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when <AOC=90∘.
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.
 View Solution
View SolutionShows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.
 View Solution
View SolutionA uniform rod of length l is rotating with constant angular speed ω as shown in figure. Choose the graph which correctly shows the variation of T with x.
_2019_CBT7_E01_017_Q01.png) View Solution
View SolutionConsider a variation of the previous problem. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistance but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity (ω) in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it.
Find the magnitude of this force when the rod makes an angle (θ) with the vertical.View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA square wire of resistance 1.3Ω and side 1cm is moving in uniform magnetic field B=1T with speed 1cm/sec as shown in figure then the current in loop is :
_2019_CBT7_E01_024_Q01.png) View Solution
View SolutionA rod of length 3l rotated with an angular velocity ω as shown in figure. The unfiorm magnetic field B is into the paper. Find
(a) VA−VC (b) VA−VD
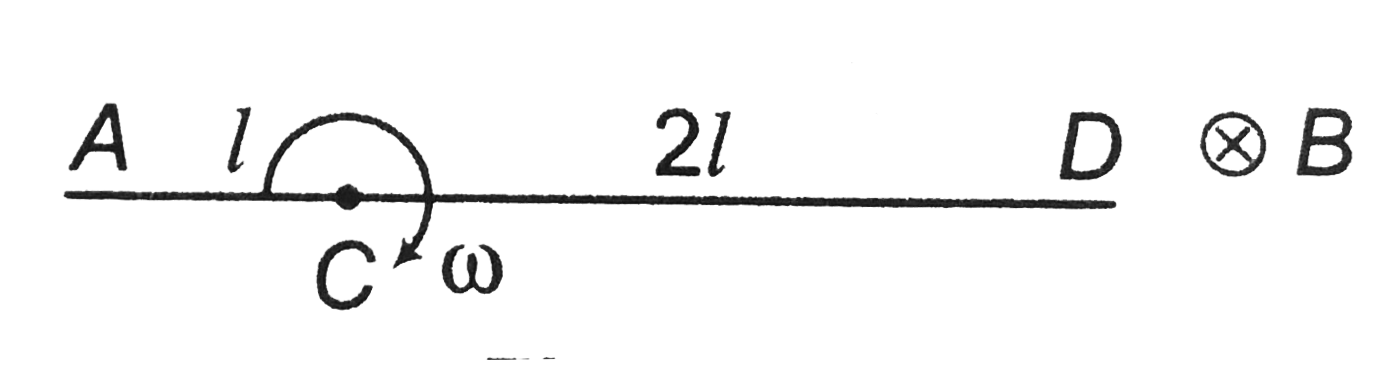 View Solution
View Solution

