Dependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by
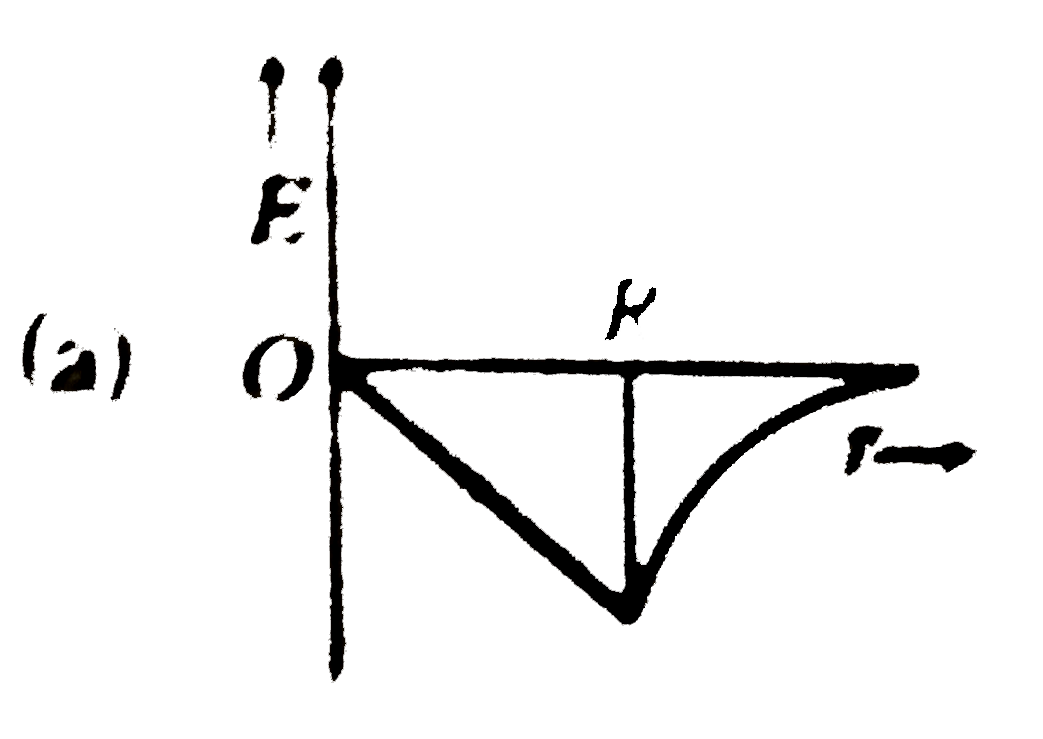
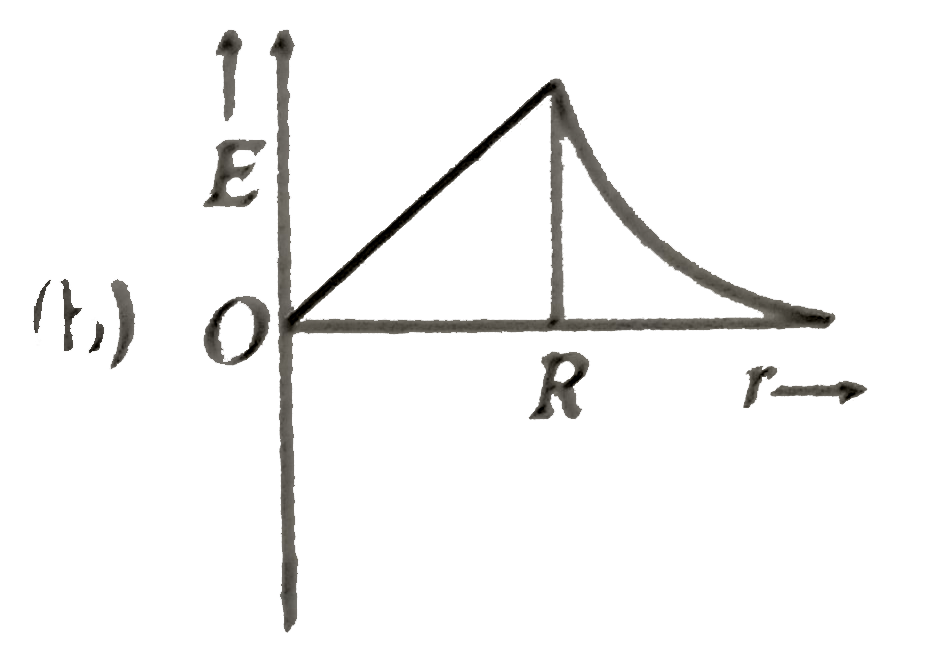
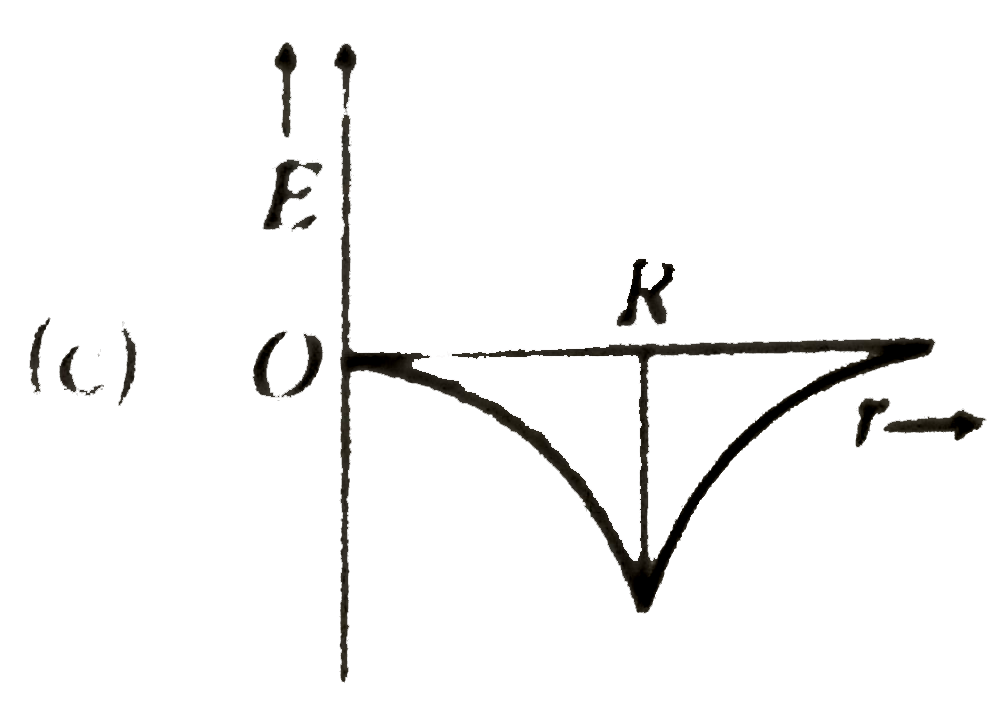
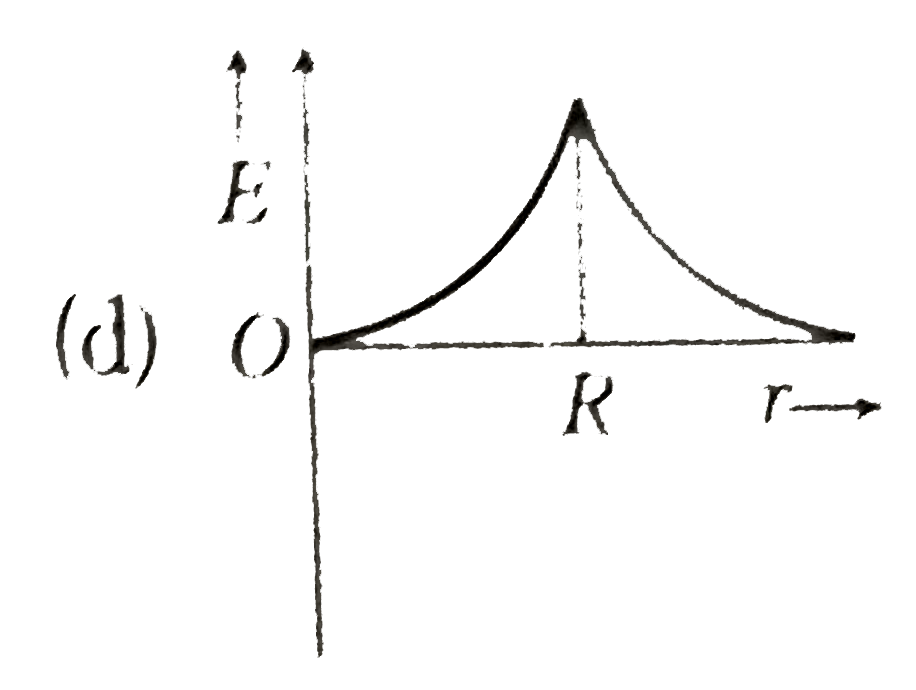
The correct Answer is:B
To solve the problem of how the intensity of the gravitational field E of the Earth depends on the distance r from the center of the Earth, we can follow these steps:
Step 1: Understand Gravitational Field Intensity
The gravitational field intensity E at a distance r from the center of the Earth is defined as the force per unit mass experienced by a small test mass placed at that distance.
Step 2: Use Newton's Law of Universal Gravitation
According to Newton's law of universal gravitation, the force F between two masses m1 and m2 is given by:
F=Gm1m2r2
where G is the gravitational constant.
Step 3: Relate Gravitational Field to Force
The gravitational field intensity E can be expressed as:
E=Fm2
where m2 is the mass of the test object. Substituting the expression for F:
E=Gm1r2
Here, m1 is the mass of the Earth.
Step 4: Analyze the Dependence on Distance
From the equation E=Gm1r2, we can see that the gravitational field intensity E is inversely proportional to the square of the distance r from the center of the Earth. This means as r increases, E decreases.
Step 5: Conclusion
Thus, the dependence of the intensity of the gravitational field E with distance r from the center of the Earth is correctly represented by the equation:
E∝1r2
Final Answer
The correct representation of the dependence of the intensity of the gravitational field E of Earth with distance r from the center of Earth is E∝1r2.
---
The gravitational field intensity E at a distance r from the center of the Earth is defined as the force per unit mass experienced by a small test mass placed at that distance.
According to Newton's law of universal gravitation, the force F between two masses m1 and m2 is given by:
F=Gm1m2r2
where G is the gravitational constant.
The gravitational field intensity E can be expressed as:
E=Fm2
where m2 is the mass of the test object. Substituting the expression for F:
E=Gm1r2
Here, m1 is the mass of the Earth.
From the equation E=Gm1r2, we can see that the gravitational field intensity E is inversely proportional to the square of the distance r from the center of the Earth. This means as r increases, E decreases.
Thus, the dependence of the intensity of the gravitational field E with distance r from the center of the Earth is correctly represented by the equation:
E∝1r2
The correct representation of the dependence of the intensity of the gravitational field E of Earth with distance r from the center of Earth is E∝1r2.
Topper's Solved these Questions
Similar Questions
The diagram showing the variation of gravitational potential of earth with distance from the centre of earth is
View SolutionA cylinderical conductor of radius R is carrying constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor , is correctly represented by the figure:
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionFollowing curve shows the variation of intesity of gravitational field (→I) with distance from the centre of solid sphere(r) :
View SolutionThe intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is 6N/kg. The gravitational potential at that point is -(in joule /kg)
View SolutionThe gravitational potential energy of a body at a distance r from the center of the earth is U. The force at that point is :
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionUsing Gauss. theorem, obtain an expression for intensity of electric field .E. at a point which is at a distance r (r>R) from the centre Cof a thin spherical shell (of radius R) carrying charge.Q.
View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View Solution
