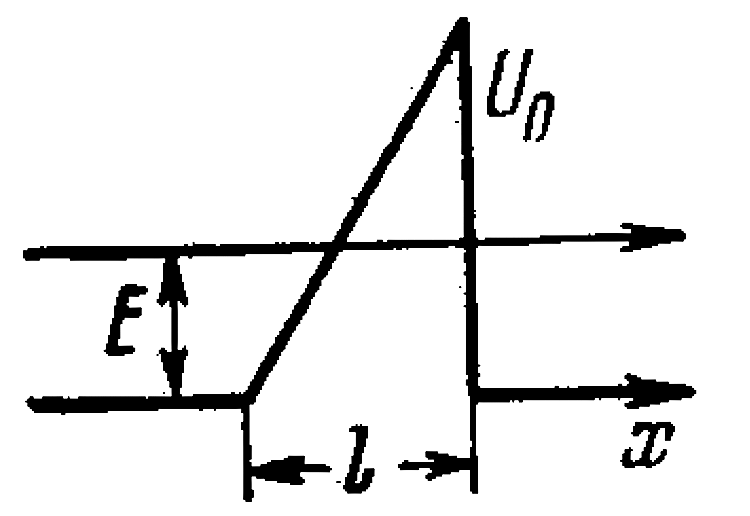
Employing Eq.(6.2e), find the probability $D$ of an electron with energy $E$ tunneling through a potential barrier of width $l$ and height $U_{0}$ provided the barrier is shaped as shown:
(a) In fig 6.4
(b) in figure 6.5.

Text Solution

Verified by Experts

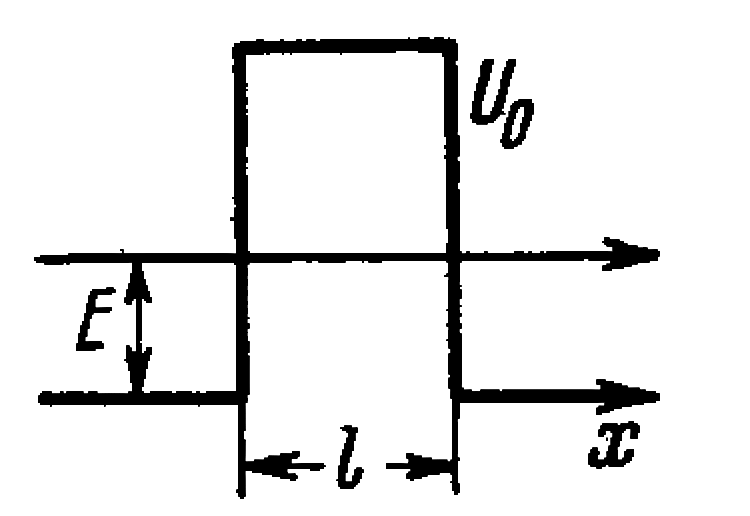
The formula is
$D \approx exp [- \frac{2}{ħ} \int_{x_{1}}^{x_{2}} \sqrt{2 m (V (x) - E) d x}]$
Here $V (x_{2}) = V (x_{1}) = E$ and $V (x) > E$ in the region $x_{2} > x > x_{1}$ .
(a) For the problem, the intergral is trivial
$D \approx exp [- \frac{2 l}{ħ} \sqrt{2 m (U_{0} - E)}]$
(b) We can without loss of generality take $x = 0$ at the point the potential begins to climb. Then
$U (x) =, ⎧ ⎪ ⎪ ⎨ ⎪ ⎪ ⎩ \begin{matrix} 0 x & < & 0 U_{0} & \frac{x}{l} & 0 x < l 0 & x > l \end{matrix}$
Then $D \approx exp ⎡ ⎣ - \frac{2}{ħ} \int_{l \frac{E}{U_{0}}}^{l} \sqrt{2 m (U_{0} \frac{x}{l} - E) d x} ⎤ ⎦$
$= exp ⎡ ⎢ ⎣ - \frac{2}{ħ} {\sqrt{\frac{2 m U_{0}}{l}}}^{l} \int_{x_{0}}^{l} \sqrt{x - x_{0}} d x ⎤ ⎥ ⎦ x_{0} = l \frac{E}{U_{0}}$
$= e p x {[- \frac{2}{ħ} \sqrt{\frac{2 m U_{0}}{l}} \frac{2}{3} {(x - x_{0})}_{0}^{3 / 2} ∣ ∣ ∣ ∣}_{x_{0}}^{3 / 2} ⎤ ⎥ ⎦$
$= exp [- \frac{4}{3 ħ} \sqrt{\frac{2 m U_{0}}{l}} {(l - l \frac{E}{U_{0}})}^{3 / 2}]$
$= exp [- \frac{4 l}{3 ħ U_{0}} {(U_{0} - E)}_{0}^{3 / 2} \sqrt{2 m}$ )]

Updated on:21/07/2023