Particle of mass m and energy E moves from the left to the potential barrier shown in figure. Find:
(a) the reflection coefficient R of the barrier for E>U0
(b) the effective penetration depth of the particles into the region x>0 for E<U0i.e., the distacne from the barrier boundary to the point at which the probability of finding a particle decreases e-fold

(a) We start from the Schrodinger equation d2Ψdx2+2mħ2(E−U(x))Ψ=0
which we write as Ψ1''+k2Ψ1=0,x<0
k2=2mEħ2
and ΨII+α2ΨII=0x>0
α2=2mħ2(E−U0)>0
It is convinient to look for solutions in the form
ΨI=eikx+Re−ikxx<0
ΨII=Aeiαx+Be−αxx>0
In region (I)(x<0), the amplitude of eikx is written as unity by conservation. In II we expect only a transmitted wave to the right, B=0 then. So
ΨII=Aeikxx>0
The boundary conditions follow from the continuity of ΨdΨdxatx=0
1+R=A
iK(1−R)=iαA
Then 1−R1+R=αk or R=k−αk+α
The reflection coefficient is the absolute square of R:
r=|R|2=∣∣∣k−αk+α∣∣∣2
(b) In this case E<U0,α2=−β2<0. Then Ψ1 is uncharged in from but
ΨII=Ae−βx+Be+βx
we must have B=0 since otherwise Ψ(x) will become unbounded as x→∞.
Inside the barrier, the particle then has probability density equal to
|ΨII|2=|A|2e−2βx
This decreases to 1e of its value in
xeff=12β=ħ2√2m(U0−E)
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Molecules And Crystals
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Elementary Particles
20 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Apaticle of mass m moves in the potential energy U shown above. Find the period of the motion when the particle has total energy E.
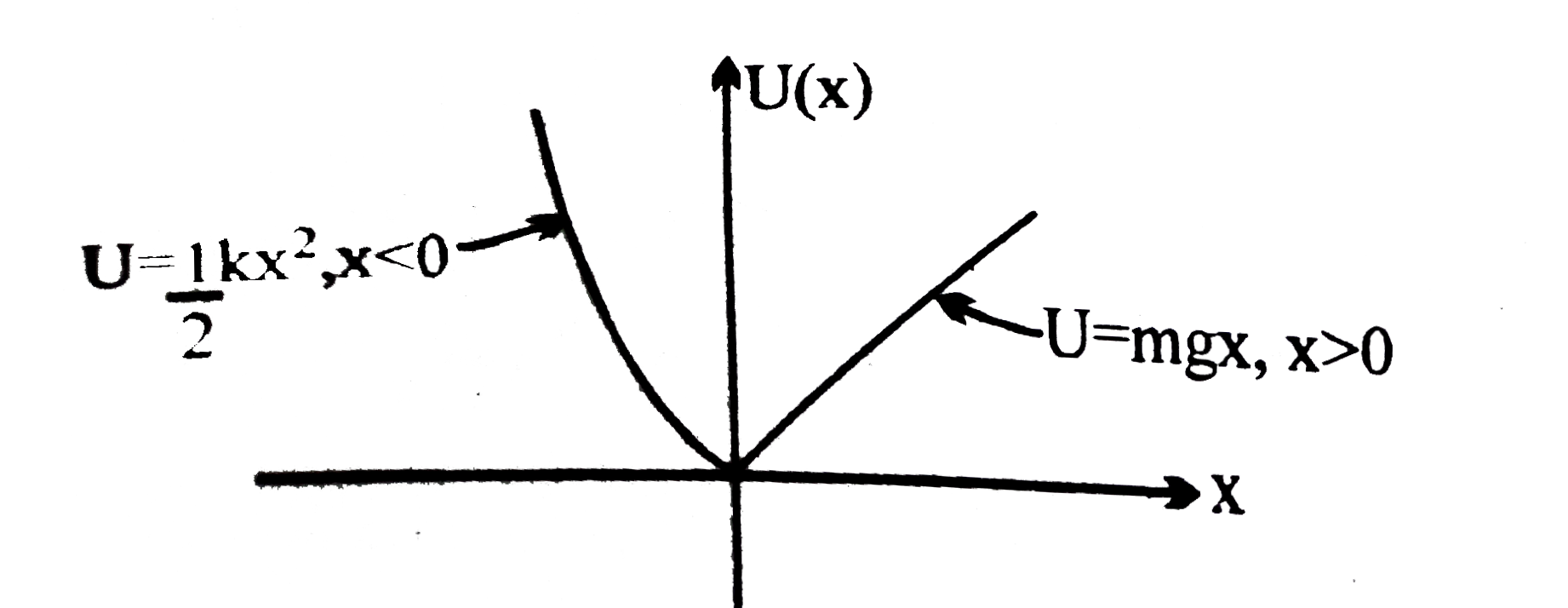
View SolutionA particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
View Solution
Knowledge Check
A particle with total energy E moves in one direction in a region where, the potential energy is U The acceleration of the particle is zero, where,
AU=EBU=0CdUdx=0Dd2Udx2=0A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
A2π√mk+4√2Emg2B2π√mkCπ√mk+2√2Emg2D2√2Emg2A potential energy curve U(x) is shown in the figure. What value must the mechanical energy Emec of the particle not exceed, if the particle is to be trapped within the region shown in graph?
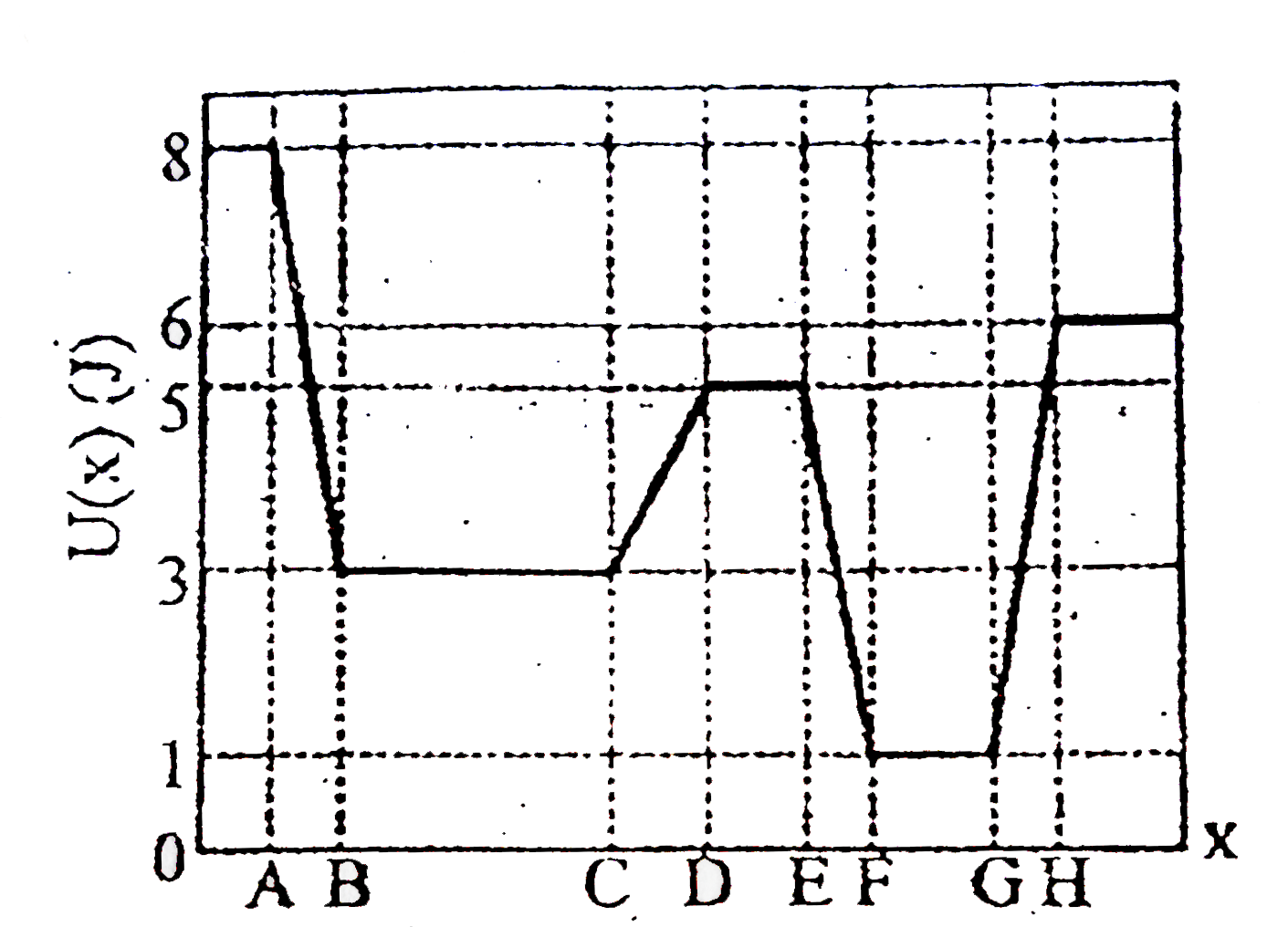 .A3JB5JC6JD8J
.A3JB5JC6JD8J
A particle of mass m moves in the potential energy U shoen above. The period of the motion when the particle has total energy E is
View SolutionA potential energy curve U(x) is shown in the figure. What value must the mechanical energy Emec of the particle not exceed, if the particle is to be trapped within the region shown in graph?
 .
.
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionA particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View Solution
