Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. the densities are ρA,ρB,ρCwithρA<ρB<ρC. The force on the base will be
maximum in vessel A
maximum in vessel B
maximum in vessel C
equal in al the vessels
The correct Answer is:D
To solve the problem of determining the force on the base of three identical cylindrical vessels containing equal masses of three different liquids with varying densities, we can follow these steps:
Step 1: Understand the relationship between mass, density, and volume
The mass m of a liquid can be expressed in terms of its density ρ and volume V using the formula:
m=ρ⋅V
For a cylindrical vessel, the volume V can be expressed as:
V=A⋅h
where A is the base area and h is the height of the liquid column.
Step 2: Express height in terms of mass and density
Since we have equal masses of the liquids in the vessels, we can rearrange the mass formula to express height h:
h=mρ⋅A
This equation shows that the height of the liquid column depends on the mass of the liquid, its density, and the base area of the vessel.
Step 3: Calculate the pressure at the base of the vessel
The pressure P at the base of the liquid column can be calculated using the hydrostatic pressure formula:
P=ρ⋅g⋅h
Substituting the expression for h from Step 2 into the pressure equation gives:
P=ρ⋅g⋅(mρ⋅A)=m⋅gA
Step 4: Calculate the force on the base of the vessel
The force F on the base of the vessel is given by the product of pressure and area:
F=P⋅A=(m⋅gA)⋅A=m⋅g
This shows that the force on the base depends only on the mass of the liquid and the acceleration due to gravity, and is independent of the density of the liquid.
Step 5: Conclusion
Since all three vessels contain equal masses of liquid, the force on the base of each vessel will be the same:
FA=FB=FC=m⋅g
Thus, the correct answer is that the force on the base will be equal in all three vessels.
Final Answer
The force on the base will be equal in all the vessels.
---
The mass m of a liquid can be expressed in terms of its density ρ and volume V using the formula:
m=ρ⋅V
For a cylindrical vessel, the volume V can be expressed as:
V=A⋅h
where A is the base area and h is the height of the liquid column.
Since we have equal masses of the liquids in the vessels, we can rearrange the mass formula to express height h:
h=mρ⋅A
This equation shows that the height of the liquid column depends on the mass of the liquid, its density, and the base area of the vessel.
The pressure P at the base of the liquid column can be calculated using the hydrostatic pressure formula:
P=ρ⋅g⋅h
Substituting the expression for h from Step 2 into the pressure equation gives:
P=ρ⋅g⋅(mρ⋅A)=m⋅gA
The force F on the base of the vessel is given by the product of pressure and area:
F=P⋅A=(m⋅gA)⋅A=m⋅g
This shows that the force on the base depends only on the mass of the liquid and the acceleration due to gravity, and is independent of the density of the liquid.
Since all three vessels contain equal masses of liquid, the force on the base of each vessel will be the same:
FA=FB=FC=m⋅g
Thus, the correct answer is that the force on the base will be equal in all three vessels.
The force on the base will be equal in all the vessels.
Topper's Solved these Questions
Similar Questions

The pressures at A and B in the atmosphere are, respectively,
View SolutionThree different liquids are filled in a U-tube as shown in figure. Their densities are ρ1,ρ2 and ρ3 respectively. From the figure we may conclude that
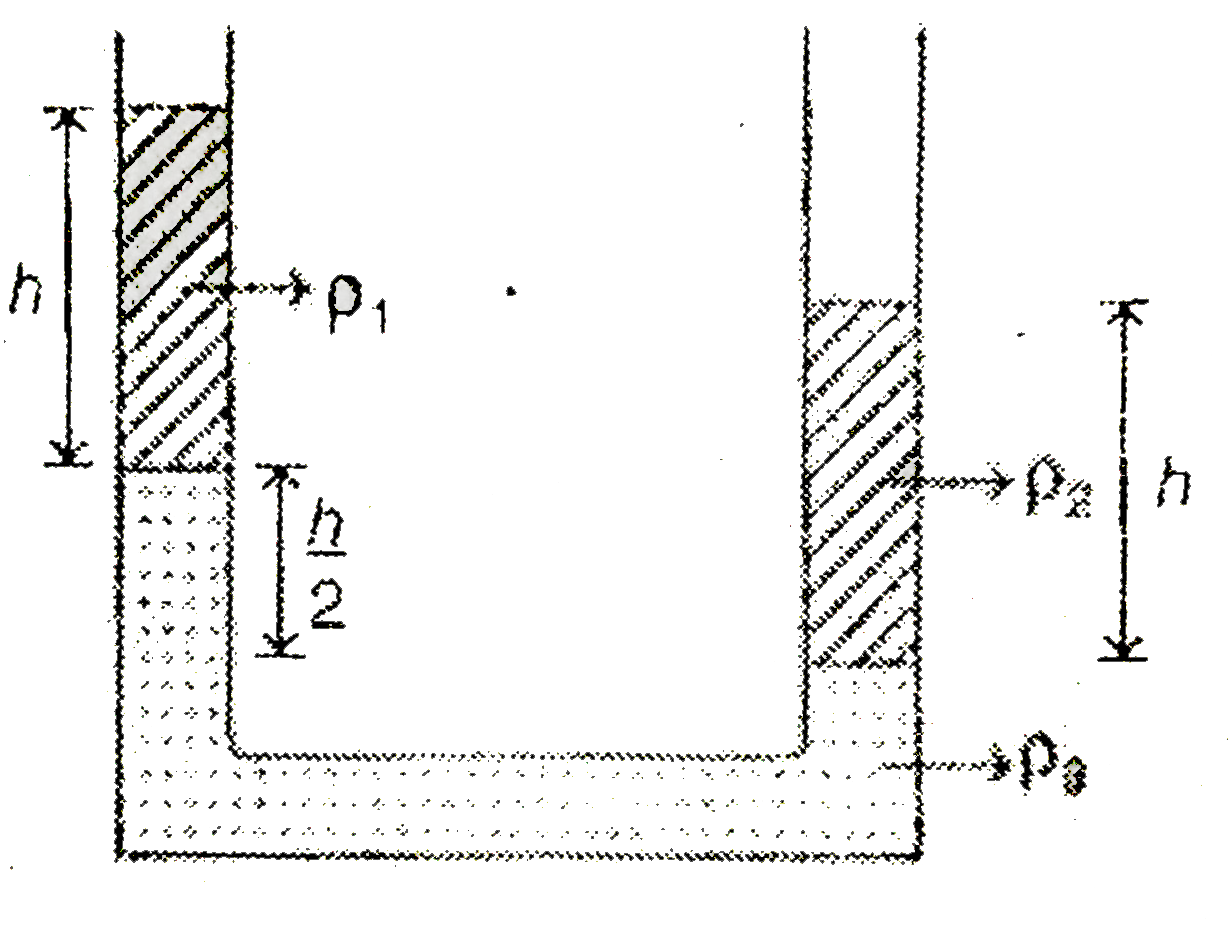
View SolutionFig shows the same block of wood floating in three different liquids A,B and C of densities ρ1,ρ2 and ρ3 respectively. Which liquid has the highest density? Give reason for your answer.

View SolutionA thin triangular glass tube containing immiscible liquids A, B, C of densities ρ,2ρ,3ρ is at rest in vertical plane. Find x.

View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View Solution
