Extraneous chagres are uniformly distributed with space density ρ>0 over a ball of radius R made of uniform istropis dielectric with permittivity ε. Find :
(a) magnitude of the electric field strength as a function of distance r from the centre of the ball, draw teh approixmate plots E(r) adn φ(r),
(b) the space and surface densities of the bound charges.
div→D=1r2∂∂rDr=ρ
r2Dr=ρr33+AD,=13ρr+Ar2,r<R
A=0 as Dr=∞ at r=0, Thus, Er=ρr3εε0
For r>R,Dr=Br2
By continuity of D, at r=R,B=ρR33
so, Er=ρR33ε0r2,r>R
φ=ρR33εr,r>R and φ=ρr26εε0+C,r<R
C=+ρR23ε0+ρR26εε0, by continuity of φ.
See answer sheet for graphs of E(r) and φ(r)
(b) ρ'=div→P=1r2∂∂r{r33ρ(1−1ε)}=−ρ(ε−1)ε
σ'=P1r−P2r=P1r=13ρR(1−1ε)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Draw a graph of electric field E(r) with distance r from the centre of the shell for 0≤r≤0 .
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View Solution
Knowledge Check
- Question 1 - Select One
A space charge of density ρ is uniformly distributed in an infinitely long cylinder of radius R Then, for any point at distance r from the axis (relative permittivity = 1)
Athe electric field is E=ρr2∈0 for 0 lt r lt RBthe electric field is E=ρR32∈0r2 for r gt RCthe electric field is E=ρr∈0 for 0 lt r lt RDthe electric field is E=ρR2∈0r for r gt R
A point charge q is located at the centre of a ball made of uniform istopic dielectric with permittivity epsilon. Find the polarizaion P as a function of the radius vector r relative to the centre of the system, as well as the chagre q' inside a sphere whose radius is less than radius of the ball.
View SolutionA charge q is uniformly distributed over the volume of a shpere of radius R. Assuming the permittively to be equal to unity throughout, find the potential
(a) at the centre of the sphere,
(b) inside the sphere as a function of the distance r from its centre.View SolutionHalf the space between two concentricv elecrodes of a sphereical capacitor is filled , as shwon in Fig, with unifrom istropic dielectric with permittively ε. The charge of the capacitor is q. Find the magnitude of the electric field strength between teh electrodes as a function of distance r from the curvature centre of teh electrodes.
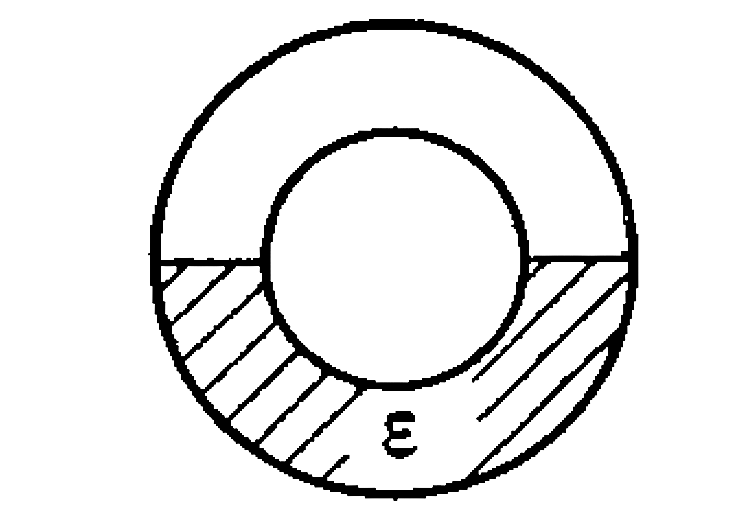 View Solution
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
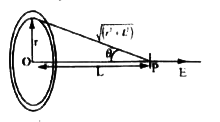 View Solution
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View Solution

