Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if m>3M2. If m = 2M, at what angle θ from vertical this happends ?
(a) 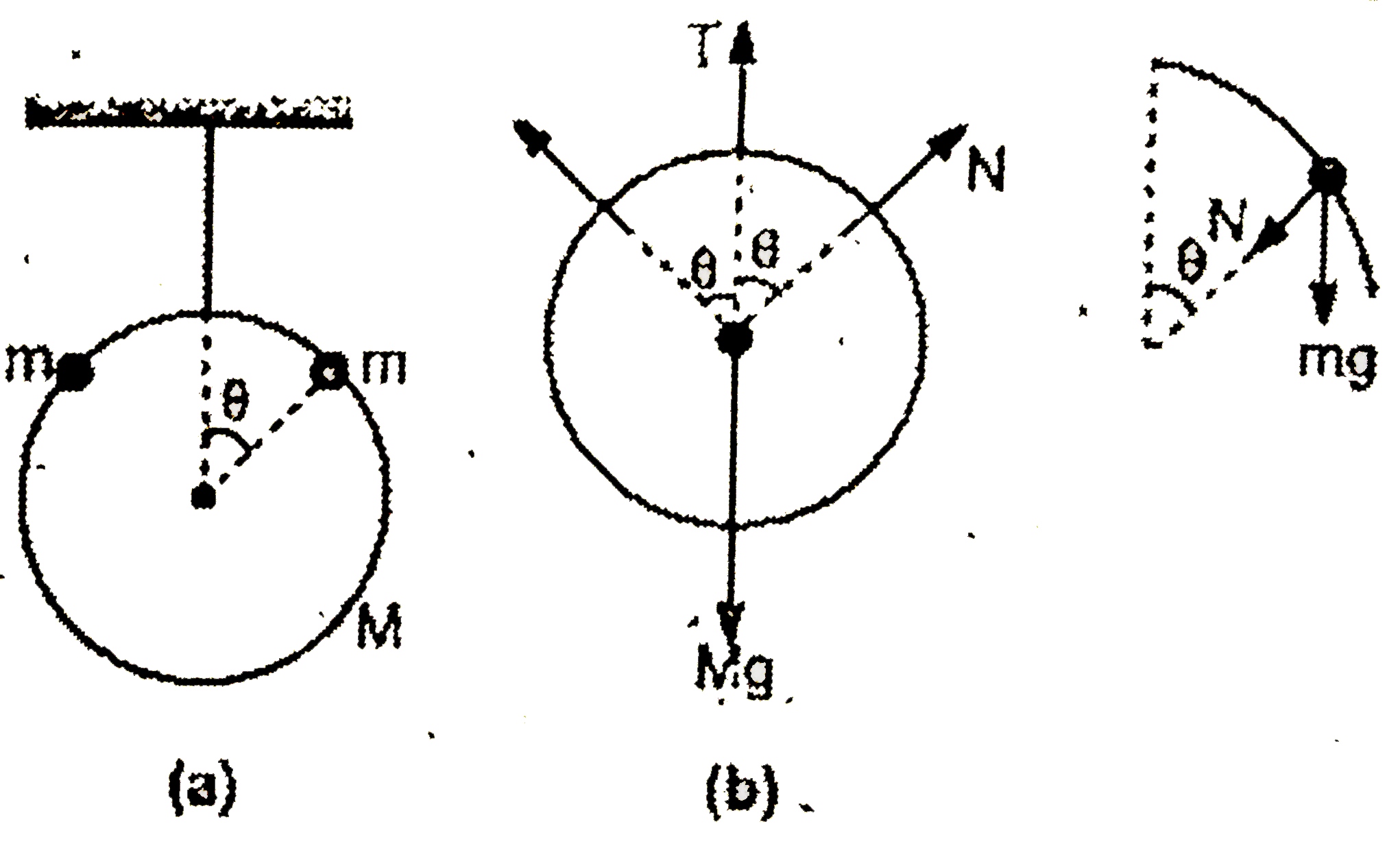
Step by step video & image solution for Fig. 3E.47 (a) shows a circular ring of mass M that hangs in a vertical plane. Two beads of mass m are released simultaneously from the top of the ring in opposite directions. There is no frictional force between the bead and the ring. Show that the ring will starts to rise if m gt (3M)/(2). If m = 2M, at what angle theta from vertical this happends ? (a) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 1
53 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 2
18 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Matching types problems
14 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2 . ltbr>
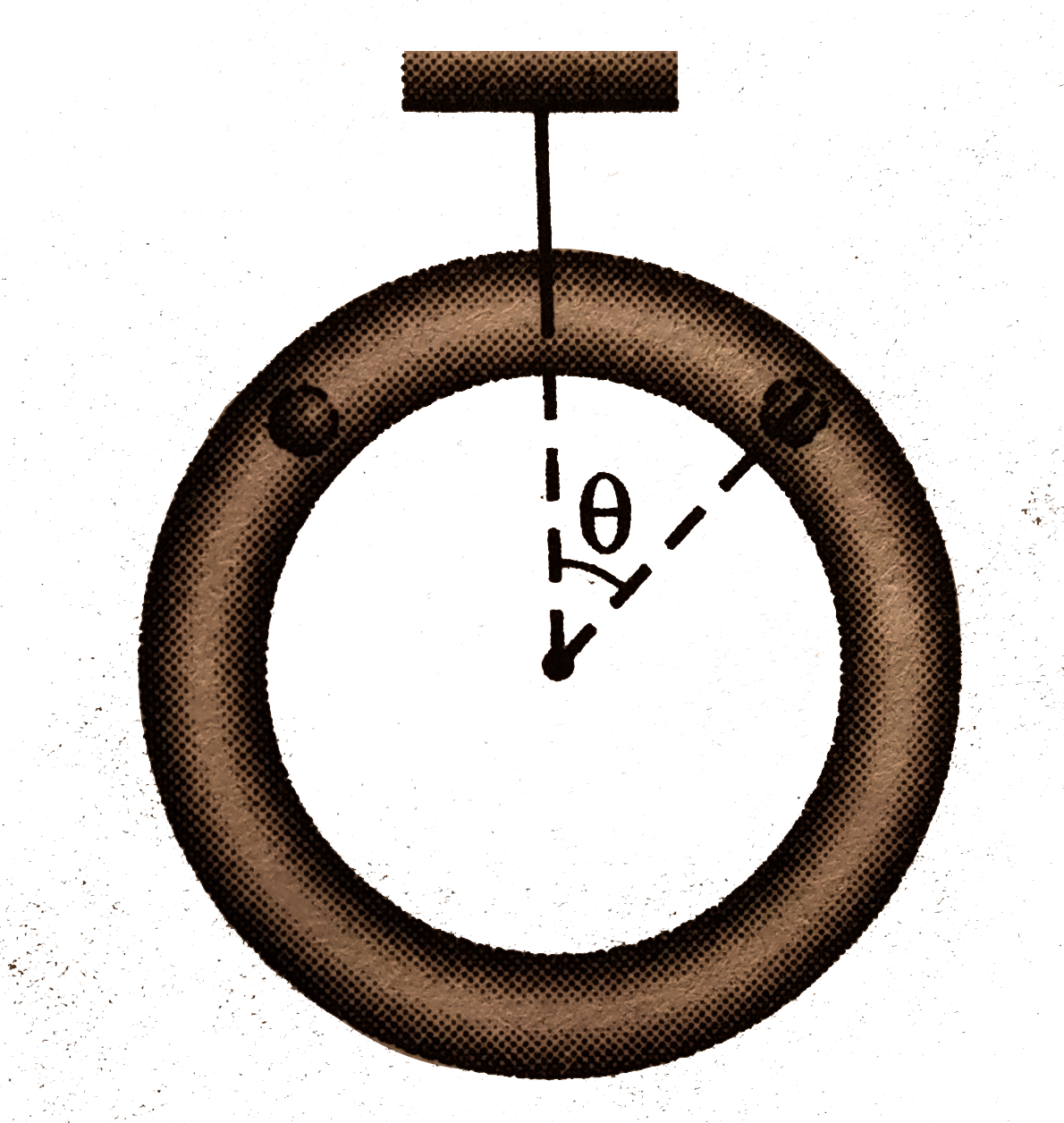
View SolutionA massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.

View Solution
Knowledge Check
A cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination θ . Both are released simultaneously from the same height h.
When these bodies roll down to the foot of the inclined plane, thenAthe mechanical energy of each body is conservedBthe velocity of centre of mass of the cylinder is 2√gh3Cthe velocity of centre of mass of the ring is √ghDthe velocity of centre of mass of each body is √2ghA cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination θ . Both are released simultaneously from the same height h.
Identify the correct statement(s)AThe friction force acting on the cylinder may be more than that acting on the ringBThe friction force acting on the ring may be more than that acting on the cylinderCIf the friction is sufficient to roll the cylinder then the ring will also rollDIf the friction is sufficient to roll the ring then the cylinder will also rollA smooth circular track of mass M is vertically hung by a string down the ceiling. Two small rings, each of mass m, are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.
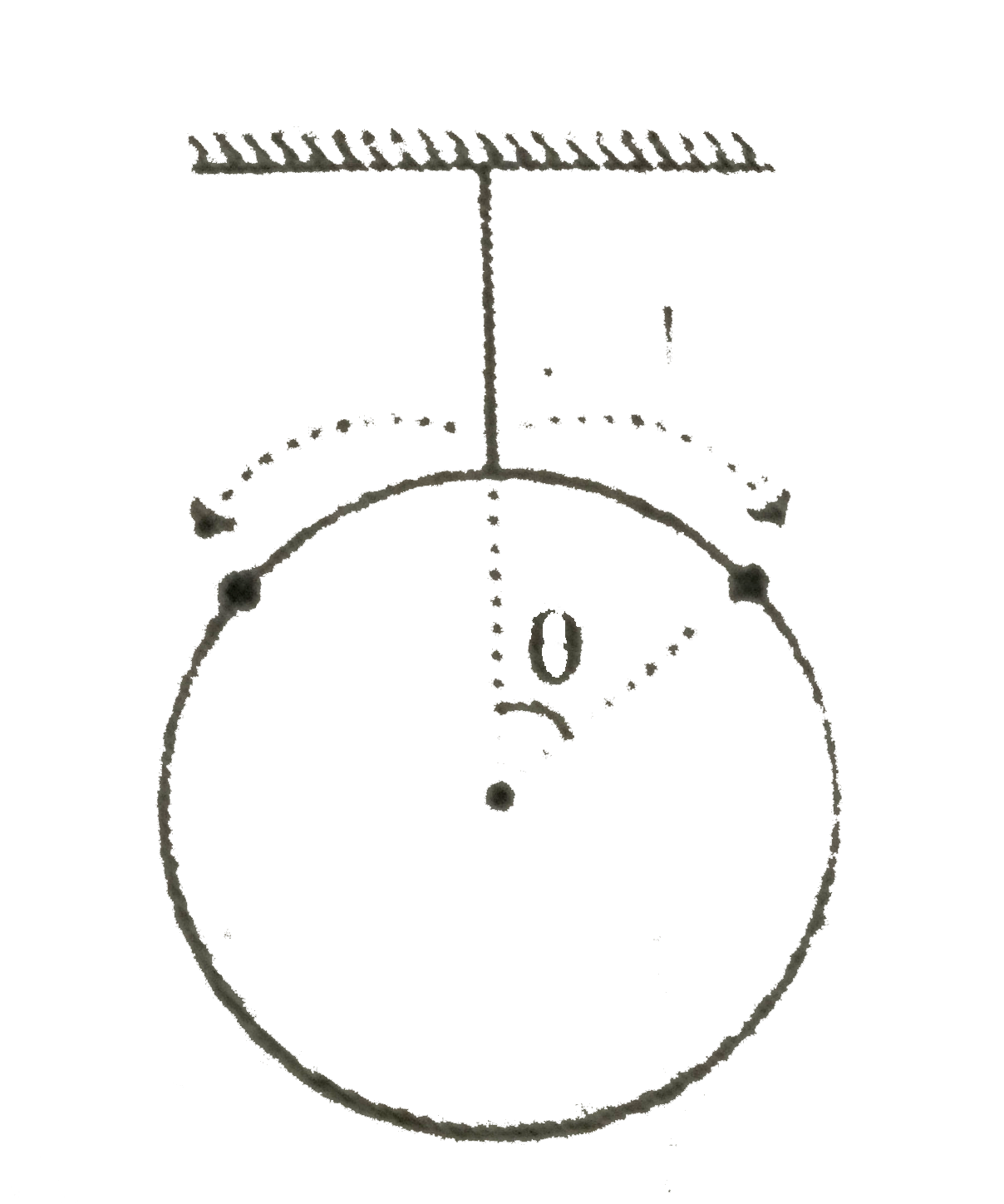 Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]
Aθ=sin−1[13(1+√1−GM3m)]Bθ=cos−1[53(1+√1−3M2m)]Cθ=cos−1[13(1+√1−3M2m)]Dθ=cos−1[13(1+√1−5M3m)]
A tube of mass M hangs from a thread and two balls of mass m slide inside it without friction (see figure). The balls are released simultaneously from the top of the ring and slide down on opposite sides. θ defines the positions of balls at any time as shown in figure
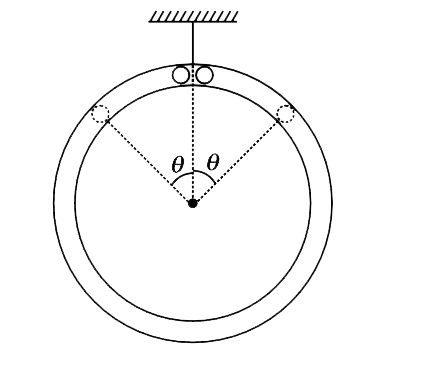
(a) Show that ring will start to rise if m≥3M2.
(b) If M=0 , find the angle θ at which the tube begins to rise.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionIn the figure shown a ring of mass M and a block of mass m are in equilibrium. The string is light and pulley P does not offer any friction and coefficient of friction between pole and M is μ. The frictional force offered by the pole to M is

View Solution