Figure-4.13 shows a water tank at a constant temperature. $T_{0}$ and a small bodyof mass m, and specific heat S at a temperature $T_{1}$ . Given that $T_{1} < T_{0}$ . A metal rod of length L, cross-sectional area A whose thermal conductivity is K is placed between the tank and the body to connect than. Find the temperature of body as a function of time. Given that the heat capacity of rod is negligible.

Video Solution

Text Solution

Verified by Experts

As temperature of water tank is constant at $T_{0}$ as it is very large, heat is conducted through the rod to the small body. If at an instant $t = t,$ the temperature ofsmall body is 7, then the rate of heat flow through the rod can be written as
Equation-(4.16) is used for heat conduction is steady state and here as the heat capacity of the rod through which heat is conducted is negligible, it does not absorb any heat thus we can assume that it is always in steady state.
If on dQ amount of heat absorption, let the temperature of small body rises hydT, then we have
Now from equation (4.16)
Now integrating the aboveexpression in proper limits, we get

Updated on:21/07/2023

One end of thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two section of length $l_{1}$ and $l_{2}$ thermal conductivities $k_{1}$ and $k_{2}$ respectively. The temerature at the interface of two section is
A $\frac{(k_{1} l_{1} T_{1} + k_{2} l_{2} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
B $\frac{(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
C $\frac{(k_{2} l_{1} T_{1} + k_{1} l_{2} T_{2})}{(k_{2} l_{1} + k_{1} l_{2})}$
D $\frac{(k_{1} l_{2} T_{1} + k_{2} l_{1} T_{2})}{(k_{1} l_{2} + k_{2} l_{1})}$
One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

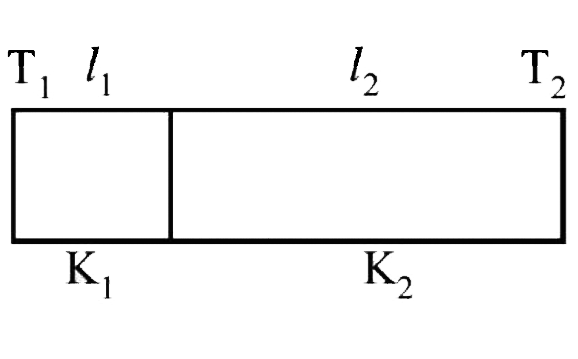A $\frac{K_{1} l_{1} T_{1} + K_{2} l_{2} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
B $\frac{K_{2} l_{2} T_{1} + K_{1} l_{1} T_{2}}{K_{1} l_{1} + K_{2} l_{2}}$
C $\frac{K_{2} l_{1} T_{1} + K_{1} l_{2} T_{2}}{K_{2} l_{1} + K_{1} l_{2}}$
D $\frac{K_{1} l_{2} T_{1} + K_{2} l_{1} T_{2}}{K_{1} l_{2} + K_{2} l_{1}}$
If two bodies at different temperatures $T_{1}$ and $T_{2}$ are brought in thermal contact, the mean temperature $\frac{T_{1} + T_{2}}{2}$ . When
Amass of two bodies are equal
Bpressure on two bodies are equal
Ctherma capacities of two bodies are equal
Dvolume of two bodies are equal