Figure shows a cylindrical tube of radius 5cm and length 20cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1atm and a temperature of 300K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600K. Let dN denote the magnitude of the normal contact force exerted by a small length dl of the cork along the periphery (see the figure). Assuming that the temperature pf the gas is uniform at any instant, calculate(dN)/(dl).

Frictional force = μN
Letthecorkmove→adistance=dl
∴Workdo≠byictionalforce=μNdl
Before that the work will not start, that
means volume remain constant.
⇒(P1T1)=(P2T2)
⇒(1300)=(P2600)
⇒(P2)=2atm
∴Extrapressure=2atm−1atm
=1atm
Workdo≠by1atm(Adl)
μNdl=[1atm][Adl]
N=⎛⎝1×(105)×π(5×(10−2))20.2⎞⎠
=(1×(105)×π×25×10−40.2)
Total circumference of work
=2πr(dNdl)=(N2πr)
=(1×(105)×π×25×10−40.2×2πr)
(1×(105)×25×10−40.2×2×5×(10−2))
=1.25×(104)Nm.
Topper's Solved these Questions
Similar Questions
A uniform tube of volume V contains an ideal monatomic gas at a uniform pressure P the temperature of the gas varies linearly along te length of the tube ad T and 2 T are the temperature at the ends.
View SolutionA cylinder fitted with a piston contains an ideal monoatomic gas at a temperature of 400K. The piston is held fixed while heat ΔQ is given to the gas, it is found the temperature of the gas has increased by 20K. In an isobaric process the same ΔQ heat is supplied slowely to it. Find the change in temperature in the second process?
View SolutionAir is filled in a bottle and it is corked at 35∘C. If the cork can come out at 3 atmospheric pressure, then upto what temperature should the bottle be heated to remove the cork ?
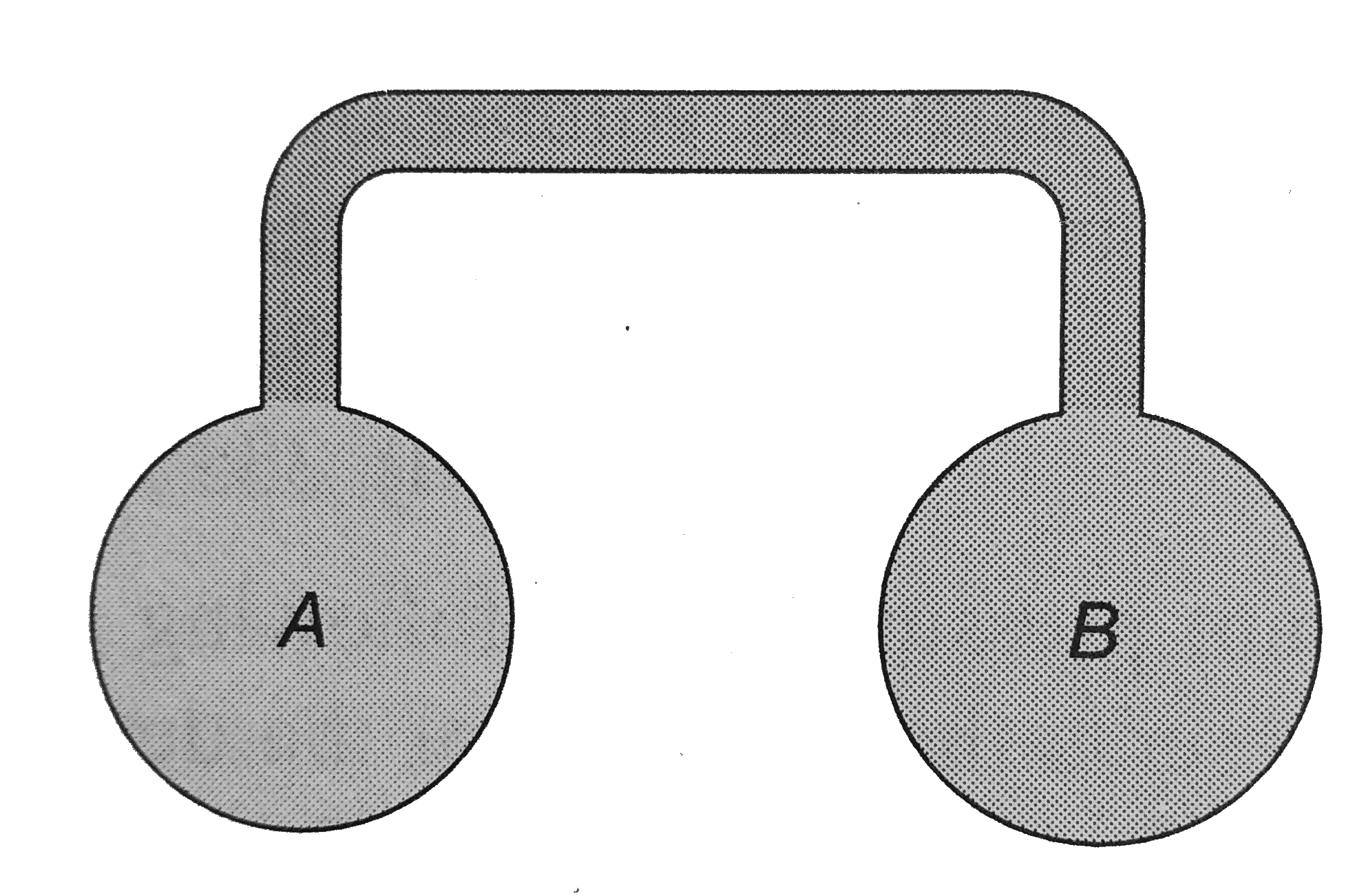
View SolutionTwo spherical vessel of equal volume are connected by a n arrow tube. The apparatus contains an ideal gas at one atmosphere and 300K. Now if one vessel is immersed in a bath of constant temperature 600K and the other in a bath of constant temperature 300K. then the common pressure will be
View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will be
View SolutionA piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
View SolutionA sealed container with gas at 2.00 atm is heated from 20.0 K to 40.0 K. The new pressure is:
View SolutionAn ideal gas is enclosed in a cylinder at pressure of 2atm and temperature, 300K. The mean time between two successive collisions is 6×10−8 s. If the pressure is doubled and temperature is increased to 500K, the mean time between two successive collisions will be close to:
View SolutionThe mean free path of the electrons in a discharge tube is 20 cm. The tube itself is 10cm long. What is the length of the Crookes dark space?
View SolutionAir is pumped into an automobile tyre's tube up to pressure pf 200kPa in the morning when the air temperature is 20∘C.During the day the temperature rises to 40∘C and the tube expand by 2%. Calculate the pressure of the air in the tube at this temperature.
View Solution
